Wielokąty I Okręgi Sprawdzian Odpowiedzi

Rozumiemy – sprawdzian z wielokątów i okręgów to dla wielu uczniów stresujący moment. Pojęcia takie jak pole, obwód, promienie, średnice, wpisane, opisane – to wszystko może wydawać się przytłaczające. Szczególnie gdy brakuje jasnych wskazówek, jak poprawnie rozwiązać zadania i z czym tak naprawdę się mierzymy. Ale spokojnie, nie jesteś sam/a w tej sytuacji. Wielu uczniów boryka się z tymi samymi wyzwaniami. Dlatego stworzyliśmy ten artykuł, aby pomóc Ci zrozumieć kluczowe zagadnienia, przeanalizować typowe błędy i przede wszystkim – przygotować się do sprawdzianu tak, abyś poczuł/a się pewnie.

Chcemy, aby ten materiał był dla Ciebie praktycznym przewodnikiem, a nie kolejnym źródłem akademickiego żargonu. Skupimy się na tym, co naprawdę ważne, podając przykłady i wskazówki, które pomogą Ci rozjaśnić wszelkie wątpliwości. Celem jest nie tylko przejście przez sprawdzian, ale także zbudowanie solidnych podstaw do dalszej nauki matematyki.

Rozkładanie Sprawdzianu na Czynniki Pierwsze: Co Właściwie Znajdziemy?

Typowy sprawdzian z wielokątów i okręgów obejmuje zazwyczaj kilka kluczowych obszarów. Zrozumienie ich struktury to pierwszy krok do sukcesu. Oto, czego możesz się spodziewać:

1. Wielokąty – Podstawy i Obliczenia

Wielokąty to figury geometryczne o prostych bokach, które tworzą zamkniętą płaszczyznę. Na sprawdzianie często pojawiają się zadania dotyczące:

Klasyfikacji wielokątów: Rozpoznawanie i nazywanie wielokątów (trójkąty, czworokąty, pięciokąty itd.). Warto pamiętać o podziale na wypukłe i wklęsłe.
Własności wielokątów: Suma kątów wewnętrznych, miara kąta wewnętrznego w wielokątach foremnych. Czy pamiętasz wzór na sumę kątów wewnętrznych w n-kącie? To (n-2) * 180°.
Obwód wielokątów: To po prostu suma długości wszystkich boków. Zazwyczaj jest to zadanie o niższym stopniu trudności, ale warto być precyzyjnym.
Pole wielokątów: Tutaj zaczyna się prawdziwa zabawa, ale i potencjalne pułapki.

Pole trójkąta: Podstawowy wzór to (a * h) / 2, gdzie 'a' to podstawa, a 'h' wysokość. Ale pamiętaj o różnych typach trójkątów i możliwych sposobach obliczenia pola (np. wzór Herona, gdy znamy wszystkie boki).
Pole prostokąta i kwadratu: Proste: a * b dla prostokąta i a² dla kwadratu.
Pole równoległoboku: a * h. Kluczowe jest tu prawidłowe zidentyfikowanie wysokości.
Pole trapezu: ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw. Trzeba uważnie dobrać podstawy i wysokość.
Wielokąty foremne: W przypadku wielokątów foremnych (wszystkie boki i kąty równe) mamy specjalne wzory, ale często wystarczy podział na mniejsze, znane figury (np. sześciokąt foremny można podzielić na 6 trójkątów równobocznych).

2. Okręgi – Serce Geometrii Płaskiej

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które są jednakowo oddalone od ustalonego punktu zwanego środkiem. Kluczowe pojęcia to:

Promień (r): Odcinek łączący środek okręgu z dowolnym punktem na okręgu.
Średnica (d): Odcinek przechodzący przez środek okręgu, o końcach na okręgu. d = 2r.
Cięciwa: Odcinek łączący dwa punkty na okręgu.
Styczna: Prosta, która ma z okręgiem dokładnie jeden punkt wspólny.
Kąty w okręgu: Kąt środkowy, kąt wpisany. Związek między nimi jest bardzo ważny: kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku.

Najczęściej spotykane obliczenia związane z okręgami to:

Obwód okręgu (długość okręgu): Obw = 2 * π * r lub Obw = π * d. Pamiętaj, że π (pi) to stała matematyczna, w przybliżeniu 3.14.
Pole koła: P = π * r². Uwaga na różnicę między "okręgiem" (linia) a "kołem" (figura wraz z wnętrzem).

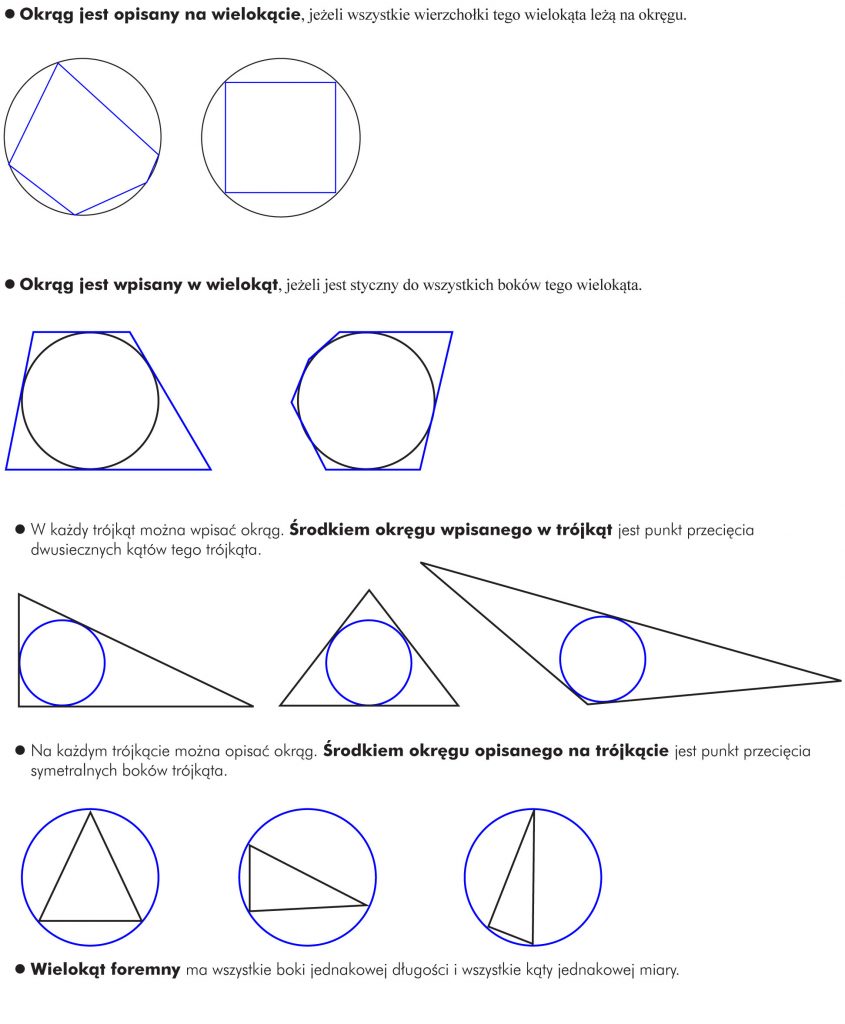
3. Figury Wpisane i Opisane

To często najbardziej problematyczna część sprawdzianów. Chodzi o wzajemne relacje między wielokątami a okręgami.

Okrąg wpisany w wielokąt: Okrąg ten jest styczny do wszystkich boków wielokąta. Promień okręgu wpisanego jest odległością od środka do boku.
Okrąg opisany na wielokącie: Okrąg ten przechodzi przez wszystkie wierzchołki wielokąta. Promień okręgu opisanego jest odległością od środka do wierzchołka.

Szczególnie ważne są tu własności wielokątów foremnych oraz specyficznych trójkątów (np. trójkąt prostokątny, w którym środek okręgu opisanego leży na przeciwprostokątnej, a jego promień to połowa przeciwprostokątnej).

Najczęstsze Błędy i Jak Ich Unikać

Analizując sprawdziany uczniów, można zauważyć powtarzające się błędy. Świadomość ich istnienia to pierwszy krok do ich eliminacji.

1. Mylenie okręgu z kołem: To podstawowy błąd, który może prowadzić do błędnych obliczeń pola i obwodu. Pamiętaj: obwód dotyczy okręgu, pole koła.

2. Nieprawidłowe identyfikowanie wysokości w równoległoboku i trapezie: Wysokość musi być prostopadła do podstawy (lub jej przedłużenia). Często uczniowie biorą za wysokość jedną z krawędzi, co jest błędne.

3. Błędy w formule potęgowania przy obliczaniu pola koła: Wzór to π * r², nie π * r czy π * 2r. To częsta pomyłka, zwłaszcza przy pośpiechu.

4. Ignorowanie jednostek: Czy zadanie wymaga podania wyniku w centymetrach kwadratowych, czy metrach? Zawsze zwracaj uwagę na jednostki!

5. Złe rozumienie "wpisany" i "opisany": Pamiętaj, że okrąg wpisany "dotyka boków", a okrąg opisany "przechodzi przez wierzchołki". Wyobraź sobie to wizualnie.

6. Błędy w obliczeniach arytmetycznych: Nawet jeśli znasz wzór, pomylisz się w mnożeniu czy dzieleniu. Dokładność to podstawa. Używaj kalkulatora ostrożnie, by uniknąć błędów przepisywania.

Strategie Przygotowania do Sprawdzianu

Teraz, gdy już wiemy, czego się spodziewać i na co uważać, czas na konkretne działania.

1. Powtórka Wzorów – Systematyczność Kluczem

Nie ucz się wszystkiego na raz. Rozbij powtórkę na mniejsze partie. Stwórz kartę wzorów. Zapisz każdy wzór kilkukrotnie, używając różnych kolorów. Umieść ją w widocznym miejscu. Codziennie poświęć 10-15 minut na przejrzenie wzorów na wielokąty, a potem na okręgi. Po kilku dniach powinny wejść Ci w nawyk.

2. Rozwiązywanie Zadań – Zrozumieć, Nie Tylko Zapamiętać

To najważniejszy etap. Zacznij od zadań prostych, potem przechodź do trudniejszych. Nie patrz od razu na odpowiedzi! Spróbuj samodzielnie. Jeśli utkniesz, wróć do teorii, poszukaj podobnego przykładu w podręczniku. Kluczowe jest zrozumienie, dlaczego dany wzór działa, a nie tylko jego mechaniczne zastosowanie.

Rada praktyczna: Weź kilka przykładowych sprawdzianów z poprzednich lat lub przygotowanych przez nauczycieli. Rozwiąż je w warunkach zbliżonych do egzaminacyjnych (z limitem czasu, bez zaglądania do notatek).

3. Analiza Błędów – Twoi Najlepsi Nauczyciele

Po każdym rozwiązanym zadaniu, szczególnie jeśli popełniłeś/aś błąd, dokładnie przeanalizuj, co poszło nie tak. Czy to błąd w obliczeniach? Złe zrozumienie polecenia? Pomylony wzór? Zapisz swoje błędy w osobnym zeszycie. Regularne przeglądanie tej listy pomoże Ci unikać tych samych pułapek w przyszłości.

Statystyka: Badania pokazują, że uczniowie, którzy poświęcają czas na analizę swoich błędów, osiągają lepsze wyniki w długoterminowej perspektywie, ponieważ budują głębsze zrozumienie materiału.

4. Wizualizacja – "Obraz Warty Tysiąca Słów"

Geometria to nauka wizualna. Rysuj! Każde zadanie zaczynaj od starannego rysunku. Oznacz wszystkie znane dane. To często pozwala dostrzec brakujące elementy lub ułatwia zrozumienie relacji między figurami. Jeśli chodzi o okręgi wpisane i opisane, rysunek jest nieoceniony.

5. Praca z Grupą – Siła Wspólnego Nauczania

Jeśli masz taką możliwość, ucz się z kolegami i koleżankami. Tłumaczenie zagadnień innym pomaga utrwalić własną wiedzę. Dyskusja nad trudniejszymi zadaniami może przynieść nowe spojrzenie i rozwiązania.

6. Uczenie się od Ekspertów – Nauczyciel i Zasoby Online

Nie bój się pytać nauczyciela! To najlepsze źródło wiedzy. Korzystaj też z rzetelnych zasobów online – filmów instruktażowych, interaktywnych ćwiczeń. Wielu edukatorów tworzy materiały, które w prosty i przystępny sposób tłumaczą skomplikowane zagadnienia.

Podsumowanie: Pewność Siebie i Sukces

Sprawdzian z wielokątów i okręgów może wydawać się trudny, ale z odpowiednim przygotowaniem jest w zasięgu ręki. Kluczem jest systematyczność, zrozumienie, a nie tylko zapamiętywanie, oraz aktywne rozwiązywanie zadań. Pamiętaj o wizualizacji, analizie błędów i korzystaniu z dostępnych zasobów.

Im więcej będziesz ćwiczyć, tym bardziej pewnie będziesz się czuć. Każde poprawnie rozwiązane zadanie buduje Twoją wiarę w siebie. W dniu sprawdzianu podejdź do niego ze spokojem i koncentracją. Zastosuj strategie, które wypracowałeś/aś podczas przygotowań. Jesteś w stanie to zrobić!

Powodzenia! Pamiętaj, że matematyka to logiczna układanka, a wielokąty i okręgi to jej fascynujące elementy.