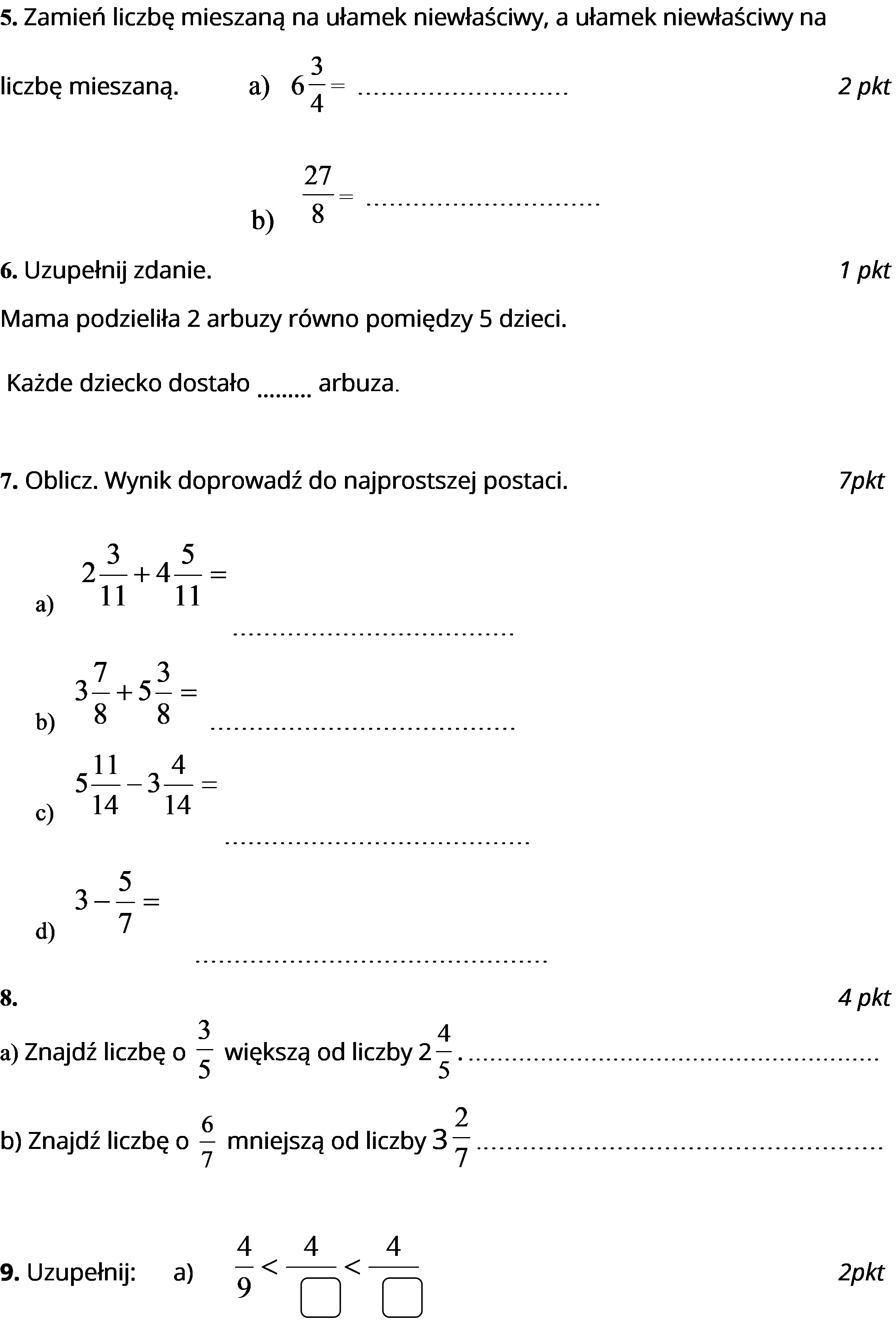Sprawdzian Kl.4 Matematyka Ułamki Zwykłe

Ułamki zwykłe stanowią fundamentalny element nauki matematyki, wprowadzany już na wczesnych etapach edukacji, w tym w klasie czwartej szkoły podstawowej. Zrozumienie tej koncepcji jest kluczowe dla dalszego rozwoju kompetencji matematycznych. Ułamek zwykły to zapis liczby, który przedstawia jedną lub więcej równych części pewnej całości. Składa się z dwóch liczb oddzielonych kreską ułamkową: liczebnika (liczba na górze, wskazująca, ile części bierzemy) i mianownika (liczba na dole, wskazująca, na ile równych części została podzielona całość). Na przykład, ułamek 1⁄2 oznacza jedną z dwóch równych części całości.
Znaczenie Ułamków Zwykłych w Klasie 4
Wprowadzenie ułamków zwykłych w klasie czwartej ma ogromne znaczenie dla dalszej edukacji matematycznej uczniów. Jest to moment, w którym dzieci zaczynają rozumieć, że liczby mogą reprezentować nie tylko pełne jednostki, ale także ich fragmenty. Jak podkreśla wielu pedagogów, wczesne i gruntowne opanowanie ułamków stanowi solidny fundament dla późniejszych zagadnień, takich jak działania na liczbach dziesiętnych, procenty, proporcje, a nawet bardziej zaawansowane koncepcje algebraiczne. Bez tego solidnego zrozumienia, uczniowie mogą napotkać poważne trudności w kolejnych latach nauki.
Badania w dziedzinie dydaktyki matematyki wielokrotnie wskazywały na to, że wiele trudności uczniów z dalszymi działami matematycznymi ma swoje źródło właśnie w nierozumieniu lub powierzchownym opanowaniu ułamków. Profesor Jo Boaler, znana badaczka w dziedzinie edukacji matematycznej, często podkreśla, że kluczem do sukcesu jest nie tylko mechaniczne nauczanie algorytmów, ale przede wszystkim budowanie intuicyjnego rozumienia koncepcji matematycznych. W kontekście ułamków oznacza to skupienie się na ich znaczeniu jako części całości, porównywaniu, dodawaniu i odejmowaniu, a nie tylko na zapamiętywaniu reguł. Sprawdzian z ułamków w klasie czwartej jest więc nie tylko oceną wiedzy, ale przede wszystkim narzędziem diagnostycznym, pozwalającym nauczycielowi ocenić stopień opanowania tej kluczowej umiejętności przez ucznia.
Wpływ na Rozwój Uczniów
Wprowadzenie ułamków zwykłych znacząco wpływa na rozwój poznawczy uczniów klasy czwartej. Dzieci uczą się abstrakcyjnego myślenia i rozumienia pojęć, które nie zawsze mają bezpośrednie, namacalne odzwierciedlenie w świecie rzeczywistym. Rozumienie, że 1⁄2 pizzy to mniej niż cała pizza, ale więcej niż jej 1⁄4, wymaga umiejętności porównywania i porządkowania liczb, które nie są liczbami naturalnymi. Ten proces rozwija logiczne myślenie, zdolność analizy i syntezy informacji.
Problemy z ułamkami mogą prowadzić do frustracji i obniżenia pewności siebie ucznia. Jeśli uczeń nie rozumie podstawowych operacji na ułamkach, takich jak sprowadzanie do wspólnego mianownika czy porównywanie, może zacząć postrzegać matematykę jako "trudną" lub "nie dla niego". Nauczyciele powinni zwracać szczególną uwagę na indywidualne potrzeby uczniów i stosować różnorodne metody nauczania, aby upewnić się, że każdy uczeń ma szansę zrozumieć te zagadnienia. Test wiedzy z ułamków zwykłych w klasie 4 powinien być zaprojektowany tak, aby uwzględniać różne style uczenia się i dawać uczniom możliwość wykazania się zrozumieniem na różnych poziomach.
Praktyczne Zastosowania Ułamków w Szkole i Życiu Codziennym
Choć może się wydawać, że ułamki zwykłe to czysto teoretyczne zagadnienie matematyczne, ich zastosowania w życiu codziennym są wszechobecne. W szkole, oprócz bezpośrednich zadań matematycznych, ułamki pojawiają się podczas lekcji przyrody (np. proporcje składników), techniki (np. odmierzanie składników), a nawet języka polskiego (np. w kontekście dzielenia tekstu na części). W kuchni ułamki są nieodłącznym elementem przepisów kulinarnych – często spotykamy się z pojęciami typu "1⁄2 łyżeczki cukru" czy "3⁄4 szklanki mąki".
Również w życiu codziennym ułamki odgrywają kluczową rolę. Kiedy kupujemy coś na przecenie, mówimy o "1⁄3 taniej". Planując posiłki, możemy dzielić tort na równe kawałki, używając właśnie pojęć ułamkowych. Nawet podczas prostych czynności, jak dzielenie się batonikiem z kolegą, intuicyjnie stosujemy zasady ułamków. Dlatego też, sprawdzian z matematyki dla klasy 4 z ułamków zwykłych powinien być skonstruowany w taki sposób, aby odzwierciedlać te praktyczne zastosowania, co pomoże uczniom dostrzec znaczenie matematyki poza szkolnymi ławkami.
"Dzieci uczą się poprzez doświadczenie i zabawę. Ułamki nie muszą być nudne! Możemy wykorzystać klocki, pokrojone owoce czy pizzę, aby w praktyczny sposób zaprezentować te koncepcje."
- cytat anonimowego nauczyciela matematyki
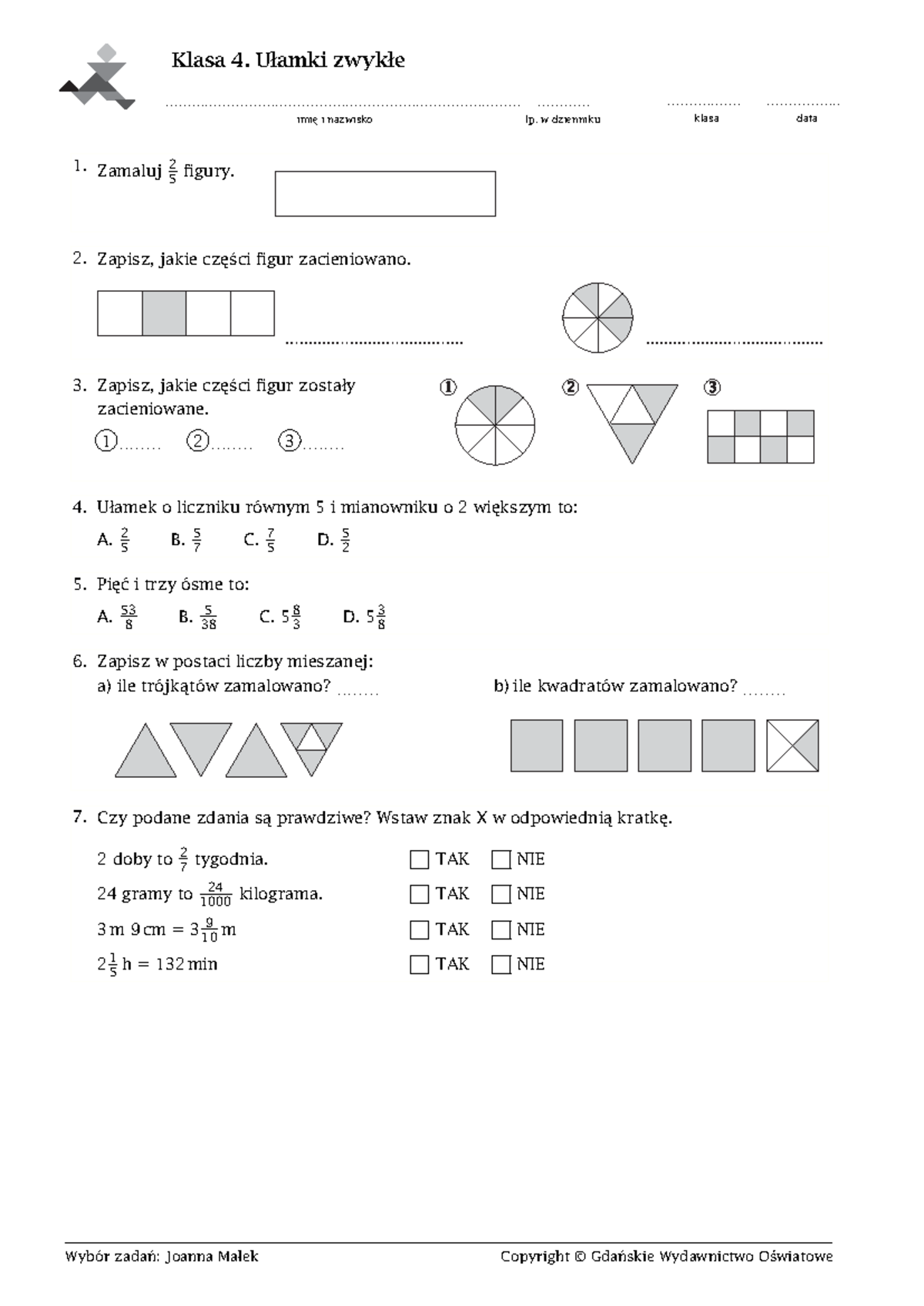
Kiedy uczniowie klas czwartych przystępują do sprawdzianu z ułamków zwykłych, powinni już posiadać podstawową wiedzę na temat ich budowy (licznik, mianownik, kreska ułamkowa) oraz umiejętność przedstawiania ułamków w postaci graficznej. Sprawdzian ten często obejmuje zadania takie jak: identyfikowanie ułamków na podstawie rysunków, porównywanie ułamków o tych samych lub różnych mianownikach, sprowadzanie ułamków do wspólnego mianownika, a także proste działania dodawania i odejmowania ułamków o jednakowych mianownikach. Umiejętność ta jest często sprawdzana poprzez ćwiczenia polegające na zamianie ułamków niewłaściwych na liczby mieszane i odwrotnie.
Podsumowując, ułamki zwykłe są nieodłącznym i kluczowym elementem programu nauczania matematyki w klasie czwartej. Ich zrozumienie ma dalekosiężne konsekwencje dla dalszego rozwoju edukacyjnego uczniów, kształtowania ich sposobu myślenia i umiejętności rozwiązywania problemów. Dobrze przeprowadzony sprawdzian z ułamków zwykłych nie tylko ocenia wiedzę, ale także motywuje do dalszej nauki i pomaga budować pewność siebie w świecie liczb.