Sprawdzian Kl 6 Pola Wielokątów Chomikuj

Witajcie drodzy uczniowie i rodzice! Dziś pochylimy się nad tematem, który często spędza sen z powiek, zwłaszcza przed sprawdzianem. Mowa o polach wielokątów dla klasy szóstej. Rozumiem, że matematyka, a zwłaszcza geometrii, może wydawać się skomplikowana. Pojawiają się wzory, liczby, rysunki – to wszystko może przytłaczać. Ale spokojnie, jesteśmy tu, aby Wam pomóc rozjaśnić ten temat. Pamiętajcie, że każda trudność jest po to, aby ją pokonać, a zrozumienie matematyki to klucz do wielu drzwi w przyszłości.

Chomikuj.pl, jako platforma edukacyjna, wie, jak ważne jest systematyczne powtarzanie materiału. Dlatego dzisiejszy artykuł będzie Waszym przewodnikiem po świecie pól wielokątów, przygotowanym specjalnie z myślą o sprawdzianie z klasy szóstej.

Zrozumieć Podstawy: Co to właściwie jest Pole?

Zanim zanurzymy się w konkretne figury, zastanówmy się, czym jest pole. Wyobraźcie sobie, że macie dywan. Pole tego dywanu to właśnie ta powierzchnia, którą on zajmuje na podłodze. W matematyce pole figury geometrycznej to miara tej powierzchni. Mierzymy je zazwyczaj w centymetrach kwadratowych (cm²) lub metrach kwadratowych (m²).

Dlaczego "kwadratowych"? Ponieważ pole wyobrażamy sobie jako pokryte kwadratami o boku 1 cm lub 1 m. Im więcej takich kwadratów zmieści się wewnątrz figury, tym większe jest jej pole. To proste, prawda?

Kluczowe Figury na Sprawdzianie: Od Prostokąta do Trójkąta

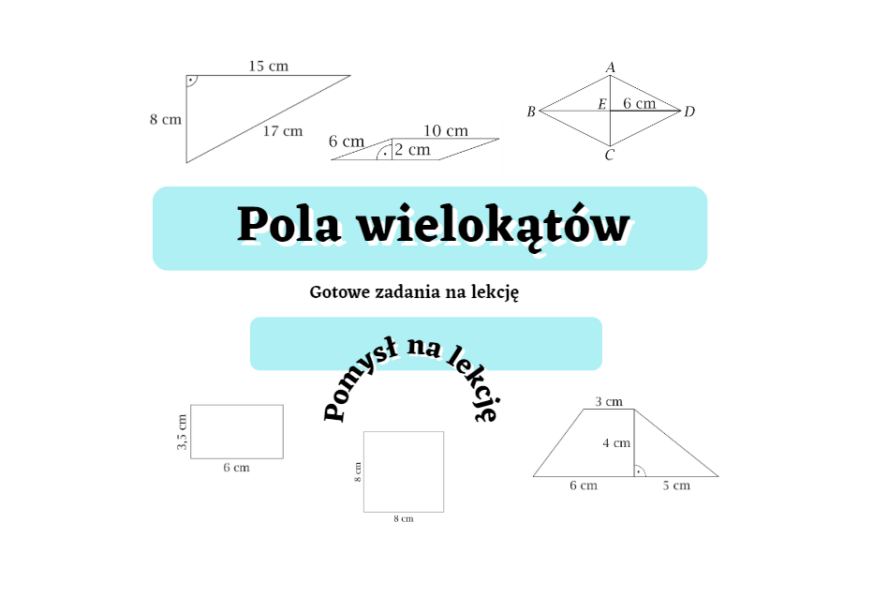
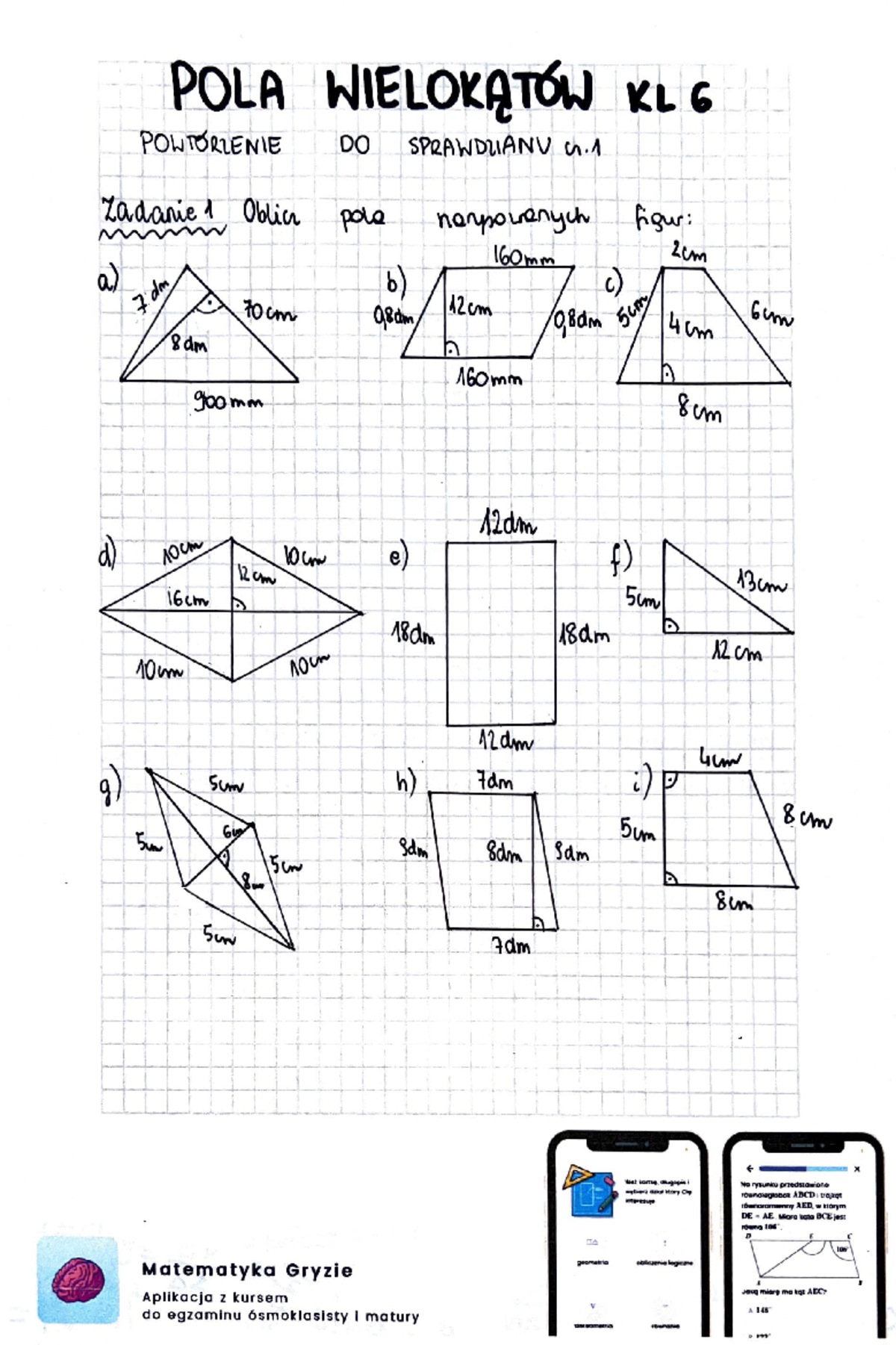
Sprawdzian z klasy szóstej zazwyczaj skupia się na kilku podstawowych wielokątach. Przygotowaliśmy dla Was zestawienie najważniejszych z nich, wraz z prostymi wyjaśnieniami, jak obliczyć ich pole.

1. Prostokąt i Kwadrat – Nasi Dobrzy Znajomi

Zacznijmy od najprostszych. Prostokąt to figura o czterech bokach, gdzie boki naprzeciwległe są równe, a wszystkie kąty są proste (90 stopni). Kwadrat to szczególny rodzaj prostokąta, gdzie wszystkie boki są równe.

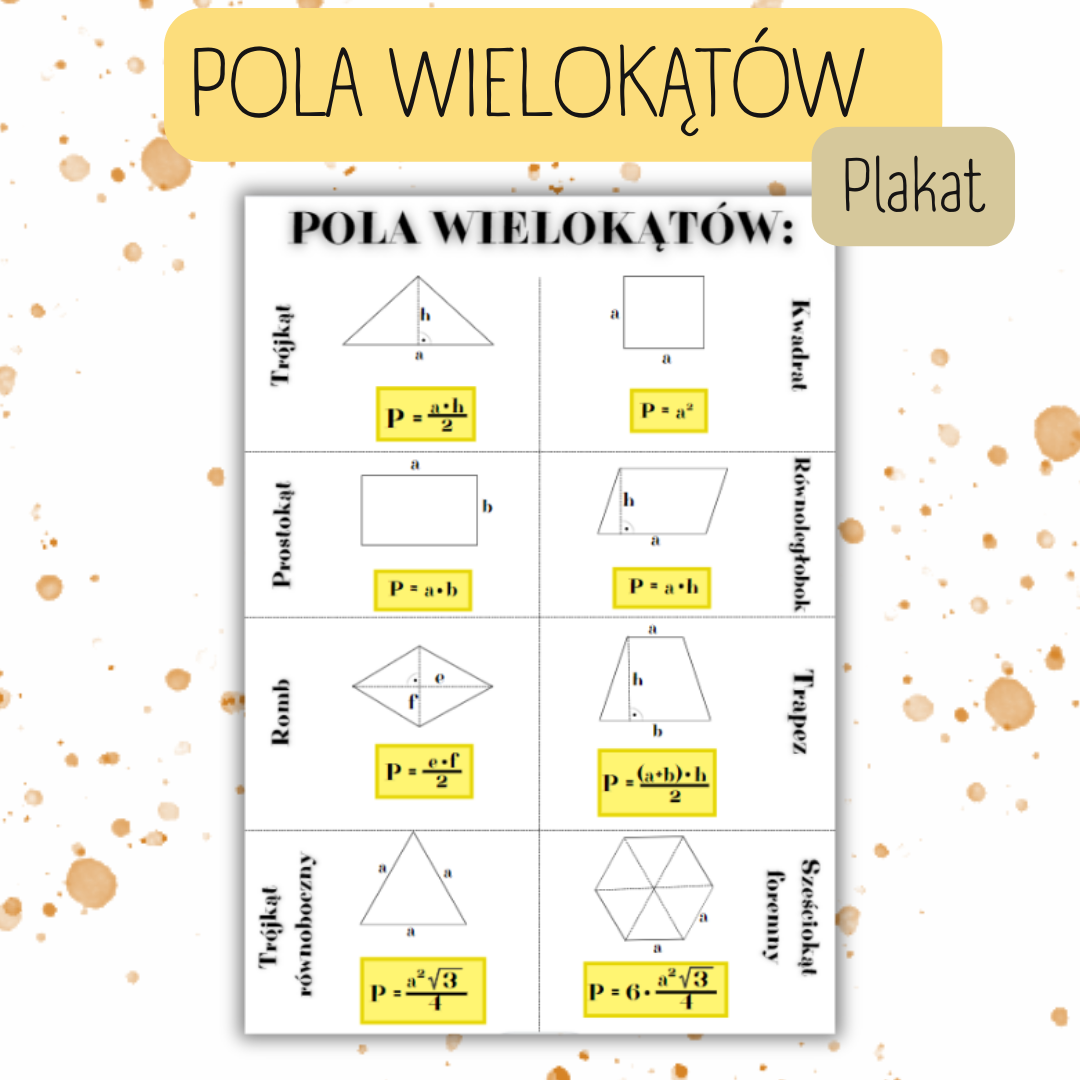
Wzór na pole prostokąta:

Pole = bok * bok lub P = a * b

Gdzie 'a' i 'b' to długości sąsiednich boków prostokąta.

Wzór na pole kwadratu:

Pole = bok * bok lub P = a * a = a²

Gdzie 'a' to długość boku kwadratu.

Przykład: Prostokąt ma boki długości 5 cm i 10 cm. Jego pole to 5 cm * 10 cm = 50 cm². Kwadrat o boku 4 cm ma pole 4 cm * 4 cm = 16 cm².

2. Równoległobok – Trochę Przechylony Prostokąt

Równoległobok to również czterobok, ale jego boki niekoniecznie muszą być prostopadłe. Kluczowe jest to, że boki naprzeciwległe są równoległe i równe.

Aby obliczyć pole równoległoboku, potrzebujemy dwóch rzeczy: długości jednego z boków (nazwijmy go podstawą) i długości wysokości opuszczonej prostopadle na tę podstawę. Ważne: wysokość nie jest równa długości drugiego boku, chyba że mamy do czynienia z prostokątem!

Wzór na pole równoległoboku:

Pole = podstawa * wysokość lub P = a * h

Gdzie 'a' to długość podstawy, a 'h' to długość wysokości opuszczonej na tę podstawę.

Przykład: Równoległobok ma podstawę o długości 8 cm, a wysokość opuszczoną na tę podstawę wynosi 5 cm. Jego pole to 8 cm * 5 cm = 40 cm².

3. Trapez – Figura o Dwóch Równoległych Bokach

Trapez to czterobok, który ma dokładnie jedną parę boków równoległych. Te równoległe boki nazywamy podstawami (jedna dłuższa, druga krótsza). Pozostałe dwa boki nie są równoległe.

Obliczenie pola trapezu może wydawać się trudniejsze, ale wzór jest logiczny. Sumujemy długości obu podstaw, dzielimy przez dwa (czyli znajdujemy ich średnią), a następnie mnożymy przez wysokość trapezu (odległość między podstawami mierzona prostopadle).

Wzór na pole trapezu:

Pole = (podstawa_1 + podstawa_2) * wysokość / 2 lub P = (a + b) * h / 2

Gdzie 'a' i 'b' to długości równoległych podstaw, a 'h' to wysokość.

Przykład: Trapez ma podstawy o długości 6 cm i 10 cm. Wysokość trapezu wynosi 4 cm. Jego pole to (6 cm + 10 cm) * 4 cm / 2 = 16 cm * 4 cm / 2 = 64 cm² / 2 = 32 cm².

4. Trójkąt – Połowa Prostokąta lub Równoległoboku

Trójkąt to figura o trzech bokach. Ważne jest, że każdy trójkąt jest połową pewnego prostokąta lub równoległoboku. To klucz do zrozumienia jego pola!

Podobnie jak w przypadku równoległoboku, potrzebujemy długości podstawy i długości wysokości opuszczonej prostopadle na tę podstawę.

Wzór na pole trójkąta:

Pole = podstawa * wysokość / 2 lub P = a * h / 2

Gdzie 'a' to długość podstawy, a 'h' to długość wysokości opuszczonej na tę podstawę.

Przykład: Trójkąt ma podstawę o długości 12 cm, a wysokość opuszczoną na tę podstawę wynosi 7 cm. Jego pole to 12 cm * 7 cm / 2 = 84 cm² / 2 = 42 cm².

Praktyczne Wskazówki na Czas Sprawdzianu

Stres przed sprawdzianem jest normalny. Ale dobra organizacja i praktyka mogą zdziałać cuda. Oto kilka rad:

• Zrozumienie, nie zapamiętywanie na pamięć. Postarajcie się zrozumieć, skąd wzięły się te wzory. Myślcie o figurach jako o kawałkach, które można złożyć w prostokąt lub połowę prostokąta.
• Rysujcie! Zanim zaczniecie liczyć, narysujcie figurę, oznaczcie boki, podstawy i wysokości. Wizualizacja bardzo pomaga.
• Zaznaczajcie dane i szukane. Na kartce ze sprawdzianu wyraźnie zaznaczcie, jakie dane macie podane (np. boki, wysokości) i czego szukacie (pole).
• Sprawdzajcie jednostki. Upewnijcie się, że wszystkie miary są w tych samych jednostkach (np. wszystko w cm lub wszystko w m) przed rozpoczęciem obliczeń.
• Powtarzajcie przykłady. Rozwiązujcie jak najwięcej przykładów z podręcznika, zeszytu ćwiczeń, a także te, które znajdziecie na Chomikuj.pl.

Profesor Ewaielka, ekspertka ds. edukacji matematycznej, podkreśla: "Kluczem do sukcesu w matematyce jest regularna, ale też świadoma praca. Nie chodzi o rozwiązywanie setek zadań bezmyślnie, ale o zrozumienie logiki stojącej za każdym wzorem i zadaniem."

Ćwiczenia na Rozgrzewkę

Zanim przyjdzie czas na sprawdzian, poćwiczmy razem!

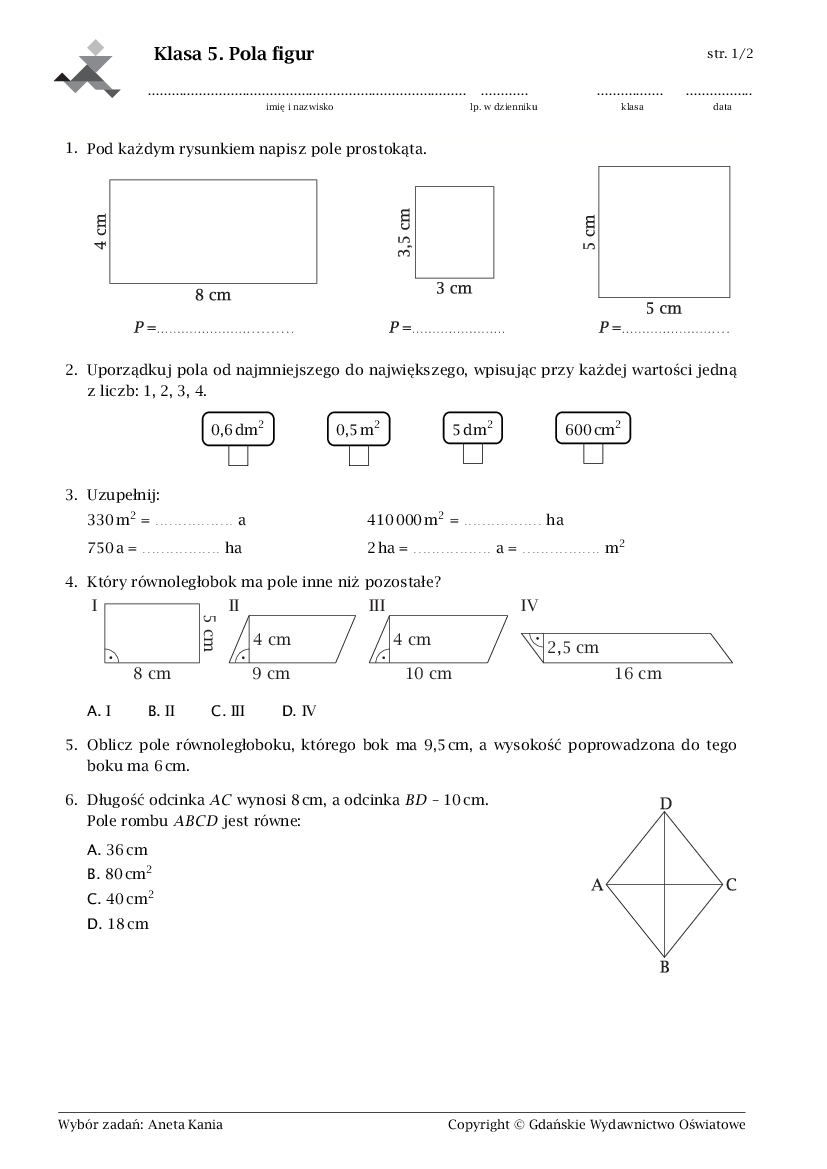
Zadanie 1 (Prostokąt): Narysuj prostokąt o bokach 7 cm i 3 cm. Oblicz jego pole.

Zadanie 2 (Kwadrat): Kwadrat ma pole 36 cm². Jaką długość ma jego bok?

Zadanie 3 (Równoległobok): Oblicz pole równoległoboku o podstawie 9 m i wysokości 5 m.

Zadanie 4 (Trapez): Długości podstaw trapezu to 11 cm i 5 cm, a jego wysokość wynosi 6 cm. Oblicz pole trapezu.

Zadanie 5 (Trójkąt): Podstawa trójkąta ma 10 dm, a wysokość opuszczona na tę podstawę to 8 dm. Oblicz pole trójkąta.

Odpowiedzi: 1. 21 cm², 2. 6 cm, 3. 45 m², 4. 48 cm², 5. 40 dm².

Codzienne Zastosowania Pola Wielokątów

Matematyka nie jest tylko dla zeszytu! Pola wielokątów mają mnóstwo praktycznych zastosowań:

• Remont i urządzanie: Kiedy chcecie kupić farbę do pomalowania ściany (pole prostokąta), wybrać odpowiedni dywan (pole prostokąta lub innego wielokąta) lub położyć płytki na podłodze (pole prostokąta, kwadratu, trapezu – w zależności od kształtu pomieszczenia i płytek).
• Ogrodnictwo: Obliczanie powierzchni działki do zasiania trawy lub posadzenia roślin.
• Gotowanie: Czasami trzeba przeliczyć proporcje składników w zależności od wielkości tortownicy (pole koła – ale to już inna historia!) lub formy do pieczenia (pole prostokąta/kwadratu).
• Projektowanie: Architekci i projektanci wnętrz na co dzień korzystają z obliczania pól różnych powierzchni.

Motywacja na Koniec

Pamiętajcie, że każdy sprawdzian to okazja do nauki i sprawdzenia swojej wiedzy. Niepowodzenia zdarzają się najlepszym, ale ważne jest, by wyciągnąć z nich wnioski i iść dalej. Wasza wytrwałość jest Waszą największą siłą.

Jeśli czujecie, że potrzebujecie więcej materiałów do nauki, Chomikuj.pl oferuje bogactwo sprawdzonych materiałów, które pomogą Wam przygotować się do każdego sprawdzianu. Nie traćcie wiary w siebie! Systematyczna praca, dobra organizacja i odrobina pozytywnego myślenia to recepta na sukces.

Trzymamy za Was kciuki! Powodzenia na sprawdzianie!