Wielokąty Foremne Sprawdzian 2 Gimnazjum

Dzisiejszy sprawdzian z wielokątów foremnych dla klasy drugiej gimnazjum może stanowić wyzwanie, ale z odpowiednim przygotowaniem i podejściem, jest jak najbardziej do opanowania.

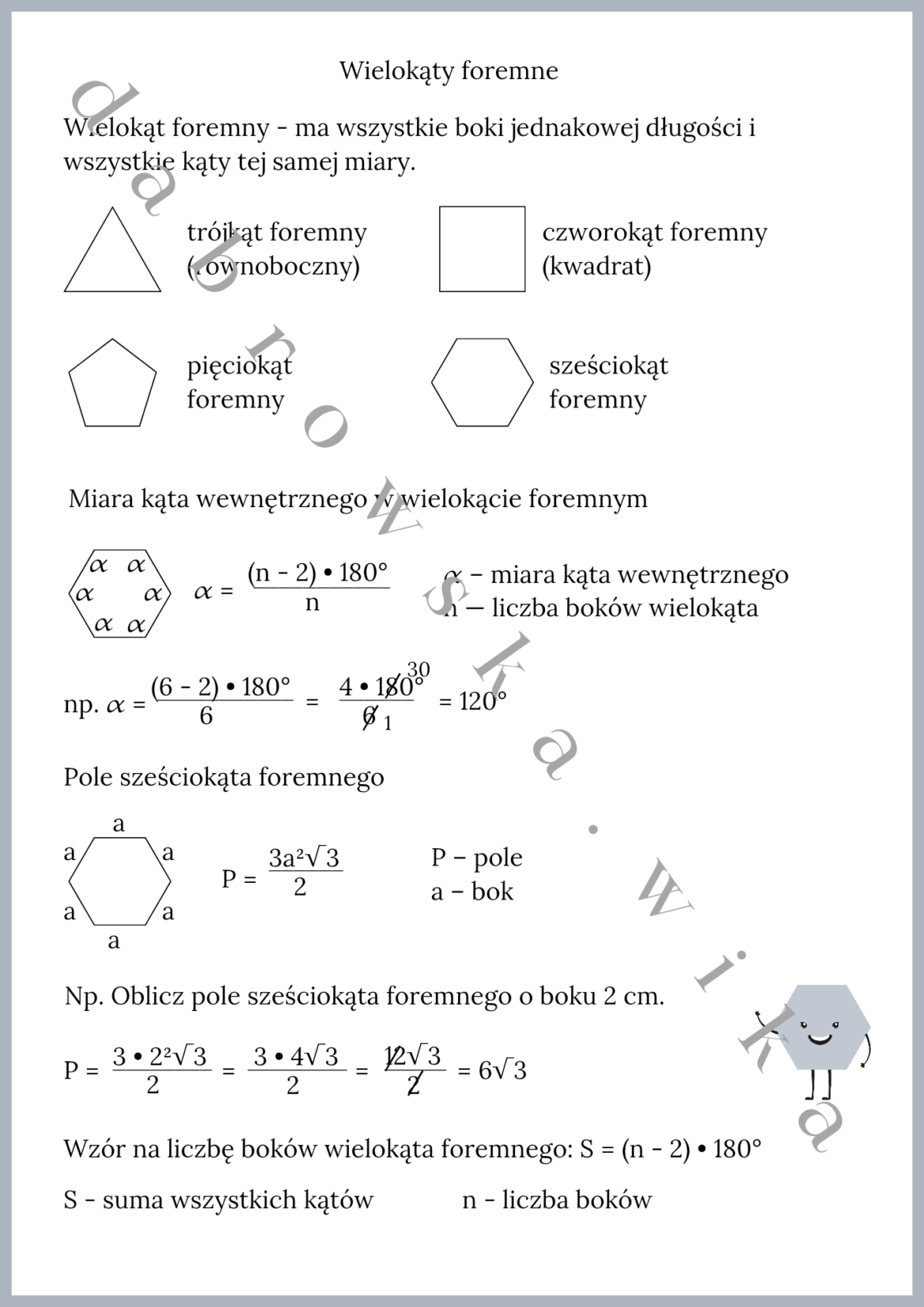
Kluczem do sukcesu jest zrozumienie podstawowych definicji i właściwości. Wielokąt foremny to taki, który ma wszystkie boki równej długości oraz wszystkie kąty wewnętrzne równej miary. To fundamentalna zasada, którą uczniowie powinni przyswoić na samym początku. Bez tego dalsze zagadnienia będą trudne do pojęcia.

Podczas lekcji warto skupić się na konkretnych przykładach, zaczynając od najprostszych, takich jak trójkąt równoboczny i kwadrat. Następnie można przejść do pięciokąta, sześciokąta i kolejnych wielokątów. Pokazywanie ich wizualizacji, rysowanie ich na tablicy, a nawet wykorzystanie modeli przestrzennych, może znacznie ułatwić zrozumienie.

Jednym z częstych błędów, jakie popełniają uczniowie, jest mylenie wielokątów foremnych z wielokątami zwykłymi, które mają tylko równe boki lub tylko równe kąty. Należy podkreślać, że muszą być spełnione oba warunki jednocześnie. Kolejną pułapką jest nieuwaga przy obliczaniu sumy kątów wewnętrznych wielokąta, która jest niezbędna do określenia miary pojedynczego kąta. Uczniowie często zapominają o wzorze lub stosują go nieprawidłowo.

Aby uczynić ten temat bardziej angażującym, można wykorzystać gry dydaktyczne lub łamigłówki. Na przykład, stworzenie zestawu kart z różnymi wielokątami i zadaniem dla uczniów, aby dopasowali je do odpowiednich opisów (np. "mam 5 boków i wszystkie kąty równe"). Można również zachęcić ich do samodzielnego rysowania wielokątów foremnych przy użyciu cyrkla i linijki, co rozwija ich umiejętności manualne i geometryczne.

Obliczanie pola i obwodu wielokątów foremnych to kolejne ważne aspekty sprawdzianu. Warto poświęcić czas na przećwiczenie stosowania odpowiednich wzorów. Przypomnienie, że obwód to suma długości boków, a pole wymaga znajomości konkretnych formuł dla każdego typu wielokąta, jest kluczowe. Można również wprowadzić pojęcie apotemy, która jest pomocna przy obliczaniu pola.

Ważne jest, aby uczniowie rozumieli, że każdy wielokąt foremny można wpisać w okrąg i opisać na nim okrąg. Ta wiedza jest często wykorzystywana w zadaniach wymagających zastosowania trygonometrii lub twierdzenia Pitagorasa, choć na poziomie drugiej gimnazjum może być ograniczona do prostszych zastosowań.

Zachęcaj uczniów do zadawania pytań. Niech czują się swobodnie, pytając o wszystko, co budzi ich wątpliwości. Powtarzanie materiału w różnych formach i podkreślanie praktycznego zastosowania geometrii w życiu codziennym, np. w architekturze czy sztuce, może dodatkowo zmotywować ich do nauki i lepszego przygotowania do sprawdzianu z wielokątów foremnych.