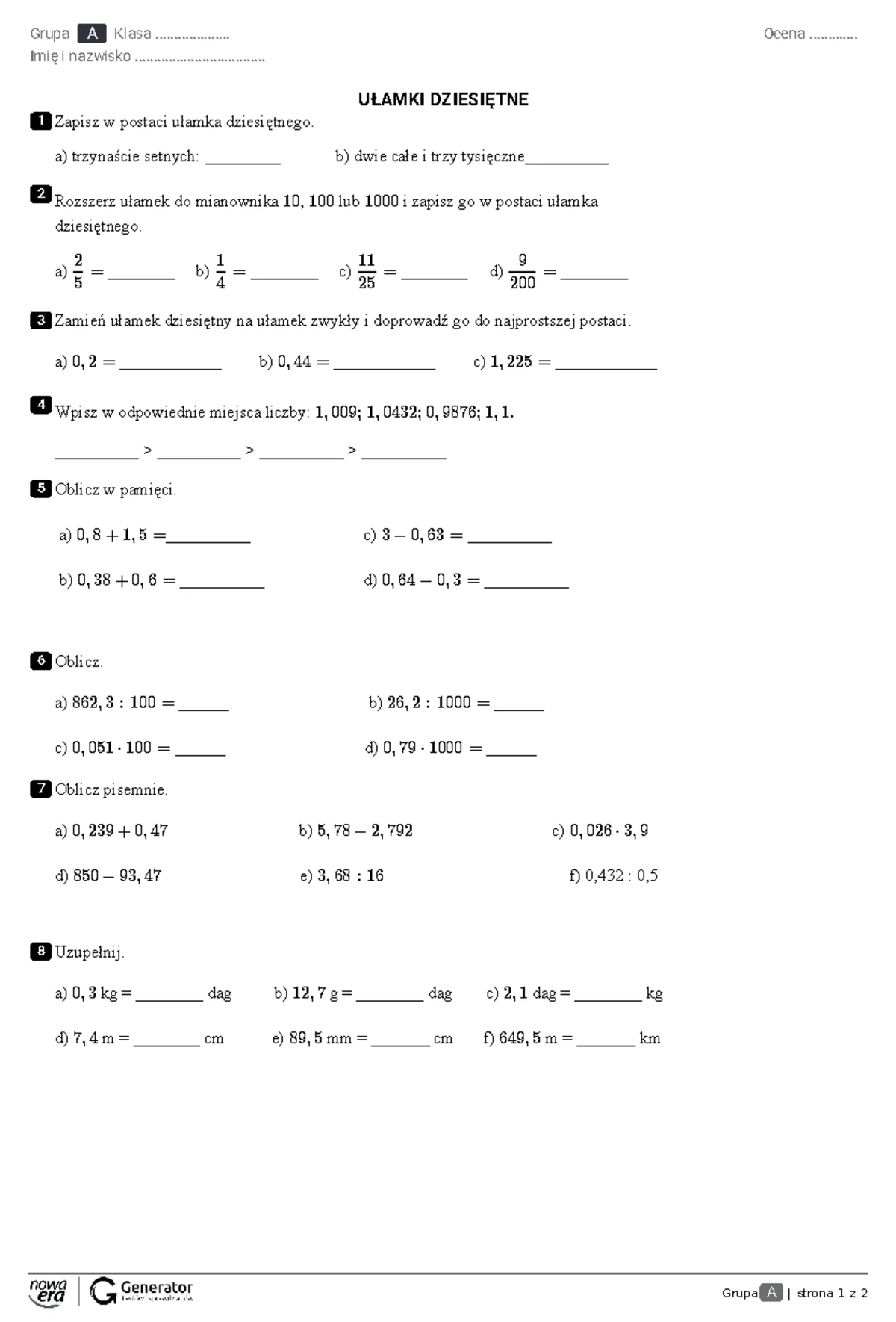
Ułamki Zwykłe Dziesiętne Sprawdzian Kl 6

Drogi Uczniu klasy szóstej,

Zbliża się sprawdzian, a słowa takie jak "ułamki zwykłe" i "ułamki dziesiętne" pojawiają się w Twojej głowie niczym kolorowe motyle, czasem przyciągające, czasem lekko onieśmielające. To naturalne. Każdy nowy etap nauki niesie ze sobą wyzwania, ale też ogromne możliwości. Pamiętaj, że ten sprawdzian to nie tylko ocena, ale przede wszystkim podróż – podróż do głębszego zrozumienia świata liczb i ich zastosowań.

Ułamki, zarówno te zwykłe, jak i dziesiętne, są fundamentem wielu zagadnień matematycznych, które będziesz poznawać w przyszłości. Już teraz widzisz ich obecność w prostych czynnościach, choć być może nie zawsze zdajesz sobie z tego sprawę. Kiedy dzielisz pizzę na równe kawałki, kiedy mówisz o połowie szklanki wody, czy kiedy odmierzysz 0.5 metra materiału na uszycie czegoś – wszędzie tam są ułamki. Są one językiem precyzji i podziału.

Nie pozwól, aby stres związał Ci skrzydła. Spójrz na ten sprawdzian jak na okazję do pokazania, ile już potrafisz, i do odkrycia, co jeszcze możesz osiągnąć. Każdy rozwiązany przykład to mały krok naprzód, każda trudność pokonana to budowanie pewności siebie.

Ułamki Zwykłe – Podstawa Rozumienia

Kiedy mówimy o ułamkach zwykłych, myślimy o podziale całości na równe części. Licznik informuje nas, ile tych części bierzemy, a mianownik, na ile równych części została podzielona całość. Czy pamiętasz, jak dodawaliśmy i odejmowaliśmy ułamki o tych samych mianownikach? To było jak dzielenie tortu na 4 kawałki i branie 1, a potem dodawanie do tego kolejnych 2. Cały czas operujemy na tych samych, równych częściach.

A co z ułamkami o różnych mianownikach? To już wymaga trochę więcej pracy – sprowadzania do wspólnego mianownika. Wyobraź sobie, że chcesz porównać dwie grupy słodyczy. Jedna jest podzielona na 3 batoniki, a druga na 6. Aby je porównać, musisz sprawić, żeby miały taką samą "jednostkę" podziału, czyli wspólny mianownik. To właśnie umiejętność znajdowania tej wspólnej płaszczyzny pozwala nam na wykonywanie bardziej skomplikowanych operacji.

Pamiętaj, że proces sprowadzania do wspólnego mianownika uczy nas cierpliwości i strategicznego myślenia. Musimy znaleźć najlepszy sposób, aby wszystko do siebie pasowało. To cenna lekcja, która przyda Ci się nie tylko w matematyce.

Ułamki Dziesiętne – Świat Precyzji

Ułamki dziesiętne to z kolei sposób na zapisanie tych samych ułamków, ale w bardziej uporządkowany sposób, wykorzystując potęgi liczby 10. Kropka dziesiętna oddziela część całkowitą od ułamkowej. Każda pozycja po przecinku ma swoje znaczenie: dziesiąte części, setne części, tysięczne części... To jakbyśmy mieli bardzo precyzyjną linijkę, gdzie możemy zaznaczyć nawet najmniejsze fragmenty.

Dodawanie i odejmowanie ułamków dziesiętnych jest bardzo intuicyjne, jeśli tylko pamiętamy o wyrównywaniu przecinków. To tak, jakbyśmy ustawiali liczby w kolumnach, aby mieć pewność, że dodajemy do siebie podobne wartości. Mnożenie i dzielenie mogą wydawać się na początku trudniejsze, ale z każdą próbą stają się coraz łatwiejsze. Kluczem jest zrozumienie, jak przesuwamy przecinek w zależności od liczby zer w drugiej liczbie.

Nauka operowania na ułamkach dziesiętnych rozwija Twoją zdolność do pracy z precyzyjnymi danymi. W życiu codziennym spotykasz je wszędzie: ceny w sklepach (np. 12.99 zł), wyniki sportowe, odległości podawane w kilometrach czy metrach. Zrozumienie ich pozwala Ci lepiej orientować się w otaczającej rzeczywistości i podejmować świadome decyzje.

Dlaczego to Ważne? Lekcje na Całe Życie

Ten sprawdzian z ułamków zwykłych i dziesiętnych to coś więcej niż tylko test wiedzy. To ćwiczenie dla Twojego umysłu, które uczy Cię:

• Analitycznego myślenia: Rozbijanie problemów na mniejsze części i szukanie logicznych rozwiązań.
• Precyzji: Dbałość o szczegóły i dokładność, co jest kluczowe w każdej dziedzinie.
• Systematyczności: Regularne powtarzanie materiału i ćwiczenie, aby osiągnąć mistrzostwo.
• Wytrwałości: Niepoddawanie się w obliczu trudności, ale szukanie nowych dróg do zrozumienia.
• Zastosowania w praktyce: Widzenie matematyki nie jako abstrakcji, ale jako narzędzia do rozwiązywania realnych problemów.

Każdy uczeń ma swoje mocne strony. Może Ty łatwiej rozumiesz wizualizację ułamków zwykłych, a może lepiej czujesz się z precyzją ułamków dziesiętnych. Oba systemy są ze sobą powiązane i wzajemnie się uzupełniają. Zrozumienie tej zależności to wielki sukces.

Pamiętaj, że każdy błąd to nie porażka, ale cenna lekcja. Zamiast się zniechęcać, zastanów się, dlaczego popełniłeś błąd. Analizując swoje pomyłki, uczysz się najwięcej i budujesz solidne podstawy na przyszłość.

Zachęcam Cię do podejścia do tego sprawdzianu z pozytywnym nastawieniem. Zaufaj swoim umiejętnościom, poświęć czas na powtórkę, a jeśli czegoś nie rozumiesz, nie wahaj się poprosić o pomoc nauczyciela lub kolegów. Matematyka to wspólna podróż, a dzielenie się wiedzą sprawia, że wszyscy stajemy się mądrzejsi.

Trzymam za Ciebie kciuki! Wierz w siebie i pamiętaj, że każdy mały sukces na tej drodze edukacyjnej buduje Twoją pewność siebie i przygotowuje do przyszłych, jeszcze większych wyzwań. Powodzenia!