Trójkąty Prostokątne Kl 8 Sprawdzian Doc

Witajcie, młodzi matematycy! Dziś zgłębimy fascynujący świat trójkątów prostokątnych. Są to trójkąty, które mają jeden kąt prosty, czyli taki, który ma dokładnie 90 stopni. To właśnie ten kąt sprawia, że trójkąty prostokątne mają wiele wyjątkowych właściwości i są niezwykle ważne w matematyce oraz w życiu codziennym.

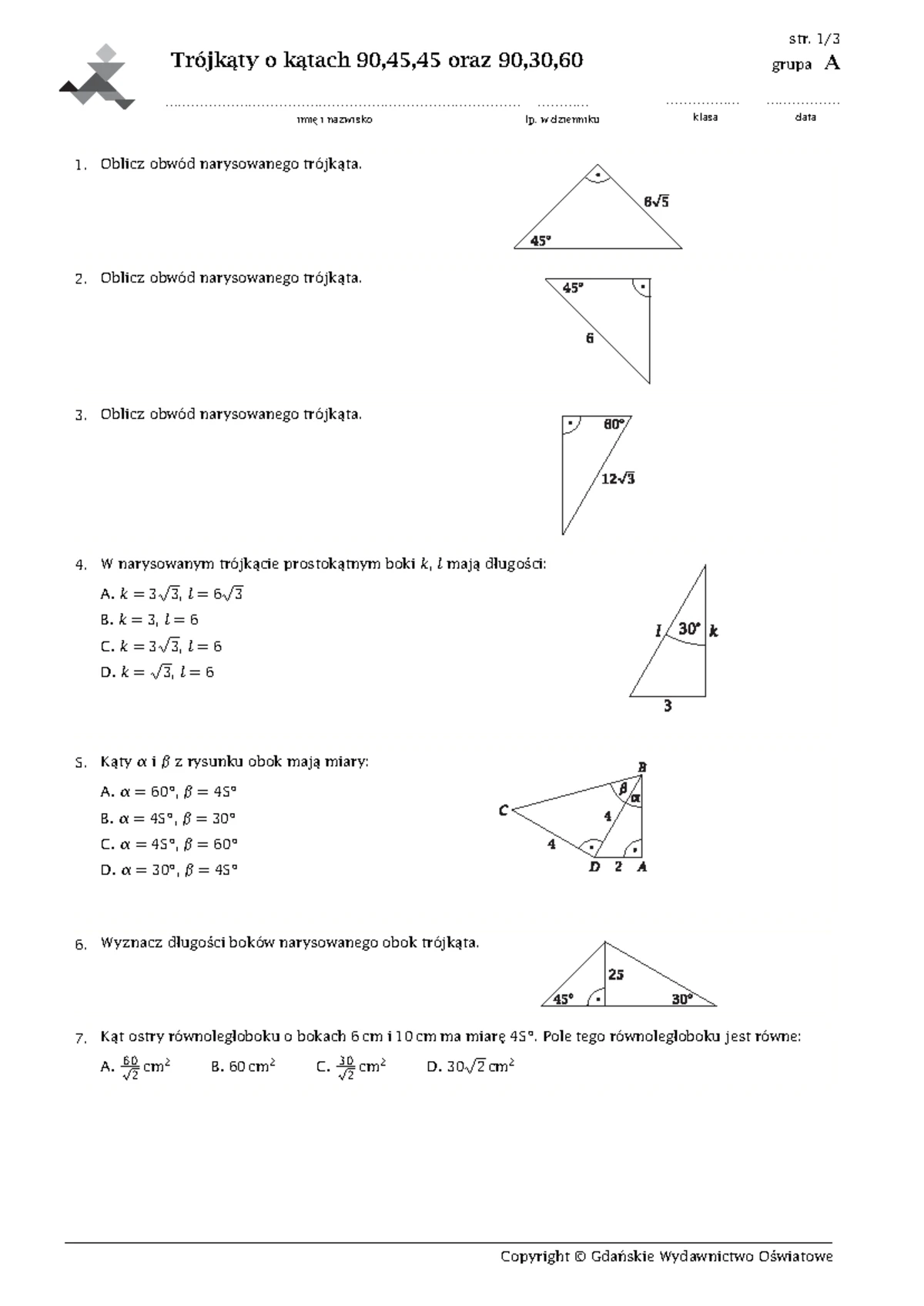
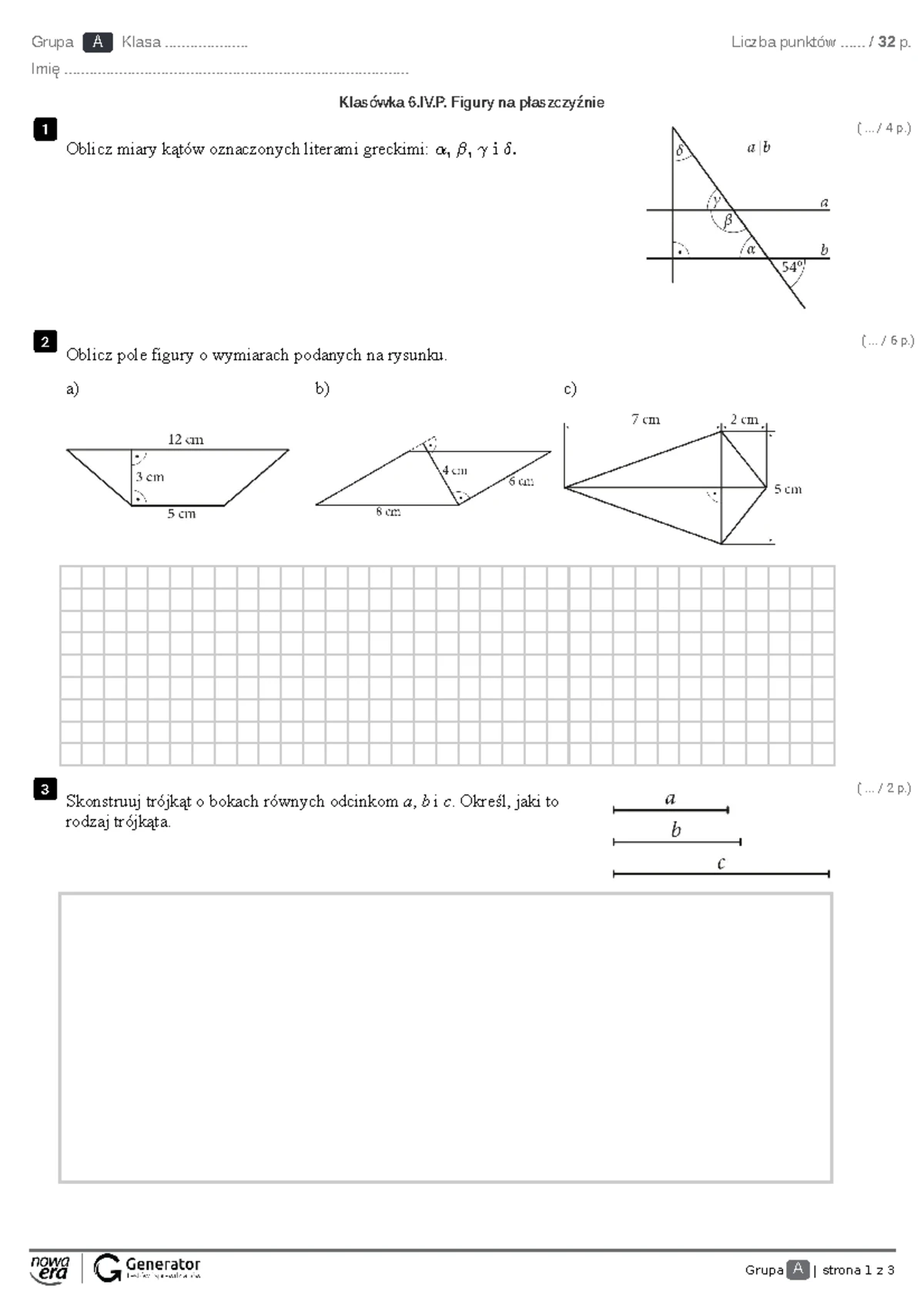
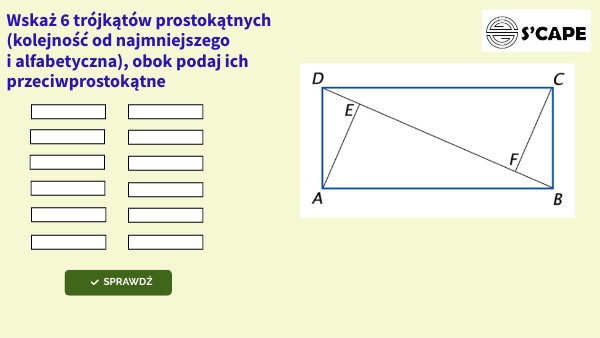
Podstawową wiedzą na temat trójkąta prostokątnego są nazwy jego boków. Dwa boki, które tworzą kąt prosty, nazywamy przyprostokątnymi. Trzeci, najdłuższy bok, który leży naprzeciwko kąta prostego, to przeciwprostokątna. Pamiętajcie, że przeciwprostokątna jest zawsze dłuższa od każdej z przyprostokątnych.

Jednym z najważniejszych twierdzeń dotyczących trójkątów prostokątnych jest twierdzenie Pitagorasa. Mówi ono, że suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Matematycznie zapisujemy to jako a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. To twierdzenie pozwala nam obliczyć długość jednego boku, jeśli znamy długości dwóch pozostałych.

Przyjrzyjmy się przykładowi. Mamy trójkąt prostokątny, którego przyprostokątne mają długości 3 cm i 4 cm. Chcemy obliczyć długość przeciwprostokątnej. Korzystając z twierdzenia Pitagorasa: 3² + 4² = c². Obliczamy kwadraty: 9 + 16 = c². Sumujemy: 25 = c². Aby znaleźć c, musimy obliczyć pierwiastek kwadratowy z 25, co daje nam 5. Zatem przeciwprostokątna ma długość 5 cm.

Trójkąty prostokątne mają także swoje specjalne rodzaje, które warto znać. Jednym z nich jest trójkąt równoramienny prostokątny. W tym trójkącie przyprostokątne mają równe długości, a kąty ostre mają po 45 stopni. Innym ważnym typem jest trójkąt egipski, który ma boki o długościach 3, 4 i 5. Jest to najprostszy przykład trójkąta prostokątnego o całkowitych długościach boków, tzw. trójka Pitagorejska.

Praktyczne zastosowania trójkątów prostokątnych są wszędzie wokół nas! Wyobraźcie sobie budowę domu – konstruktorzy używają ich do sprawdzania kątów prostych w ścianach i fundamentach. Architekci stosują je do projektowania schodów czy dachów. W nawigacji, na przykład w GPS, obliczenia odległości często opierają się na zasadach trójkątów prostokątnych.

Nawet w codziennym życiu możemy dostrzec ich obecność. Kiedy wieszacie obraz na ścianie i chcecie, aby wisiał prosto, często korzystacie z kątownika, który ma kształt trójkąta prostokątnego. Rozkładać koc na plaży tak, by zajmował jak najwięcej miejsca pod słońcem, również może wymagać myślenia o kształtach i wymiarach, czasem opierając się na geometrii trójkątów prostokątnych.

Znajomość trójkątów prostokątnych i twierdzenia Pitagorasa jest kluczowa do dalszej nauki matematyki, a także do zrozumienia wielu zjawisk fizycznych i technicznych. Pamiętajcie o praktyce – im więcej zadań rozwiążecie, tym pewniej poczujecie się z tym tematem. Powodzenia podczas sprawdzianu!