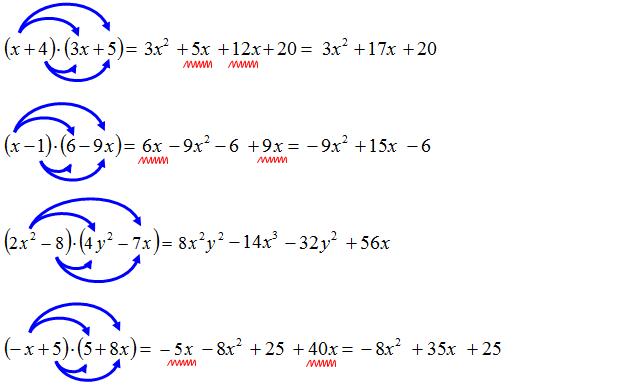Sumy Algebraiczne Sprawdzian 2 Technikum

Witajcie, przyszli mistrzowie Sumy Algebraicznej! Ten artykuł pomoże Wam zrozumieć kluczowe zagadnienia ze Sprawdzianu 2 w technikum. Pomyślcie o tym jak o budowaniu z klocków – każdy element ma swoje miejsce i cel.
Zacznijmy od wielomianów. Wyobraźcie sobie wielomian jako składankę. Każdy kawałek tej składanki to wyraz. Na przykład, w składance 3x² + 2x - 5, mamy trzy kawałki: 3x², 2x i -5. Każdy wyraz ma swój współczynnik (liczbę przed literką, jak 3 czy 2) i zmienną (litery, np. x) podniesioną do jakiejś potęgi. Wyraz -5 to taki samotny koralik bez zmiennej, nazywamy go wyrazem wolnym.
Teraz dodawanie i odejmowanie wielomianów. To jak sortowanie klocków według kształtu i koloru. Możecie dodawać tylko te klocki, które do siebie pasują. W świecie wielomianów, to oznacza łączenie wyrazów podobnych. Wyrazy podobne mają tę samą zmienną podniesioną do tej samej potęgi. Na przykład, 3x² i -7x² to wyrazy podobne, bo oba mają x². Możecie je dodać lub odjąć, tak jakbyście łączyli grupy czerwonych klocków. 2x i 5x też można połączyć, bo oba mają x w pierwszej potędze. Ale 3x² i 2x to już inne kształty – nie da się ich tak po prostu dodać.
Wyobraźcie sobie dwie grupy zabawek. Jedna grupa ma 3 czerwone samochodziki i 2 niebieskie klocki. Druga grupa ma 5 czerwonych samochodzików i 1 zieloną łódkę. Gdy chcecie je połączyć, możecie policzyć wszystkie czerwone samochodziki razem (3 + 5 = 8) i wszystkie niebieskie klocki (tylko 2). Zielonej łódki nie możecie połączyć z niebieskim klockiem, bo są różne. To właśnie jest dodawanie wielomianów!
Przejdźmy do mnożenia wielomianów. To jak rozpakowywanie prezentów. Gdy mnożycie jeden wielomian przez drugi, musicie każdy wyraz z pierwszego wielomianu pomnożyć przez każdy wyraz z drugiego wielomianu. To jakby każdy klocek z pierwszej paczki musiał spotkać się z każdym klockiem z drugiej paczki. Na przykład, jeśli mnożycie (a + b) przez (c + d), to najpierw a mnoży się przez c (dajecie ac), potem a przez d (dajecie ad). Następnie b mnoży się przez c (dajecie bc) i na końcu b przez d (dajecie bd). Wynik to ac + ad + bc + bd. Jakbyście tworzyli nowe zestawy, gdzie każdy element z jednej grupy łączy się z każdym elementem z drugiej.
Pomyślcie o mnożeniu jak o tworzeniu nowych połączeń. Macie grupę jabłek i grupę gruszek. Każde jabłko chcesz pokazać każdej osobie, która ma gruszkę. Kiedy skończycie, każdy miał okazję zobaczyć i jabłko, i gruszkę. To daje nam wiele różnych kombinacji.
Pamiętajcie, że podczas mnożenia potęg z tą samą podstawą, potęgi się dodają. Jeśli macie x² * x³, to tak jakbyście mnożyli x*x przez x*x*x, co daje x*x*x*x*x, czyli x⁵. Potęgi dodajemy: 2 + 3 = 5. To proste zasady, które pomogą Wam w rozwiązywaniu zadań. Ćwiczenie czyni mistrza, więc im więcej przykładów rozwiążecie, tym lepiej będziecie rozumieć te "składanki" algebraiczne!