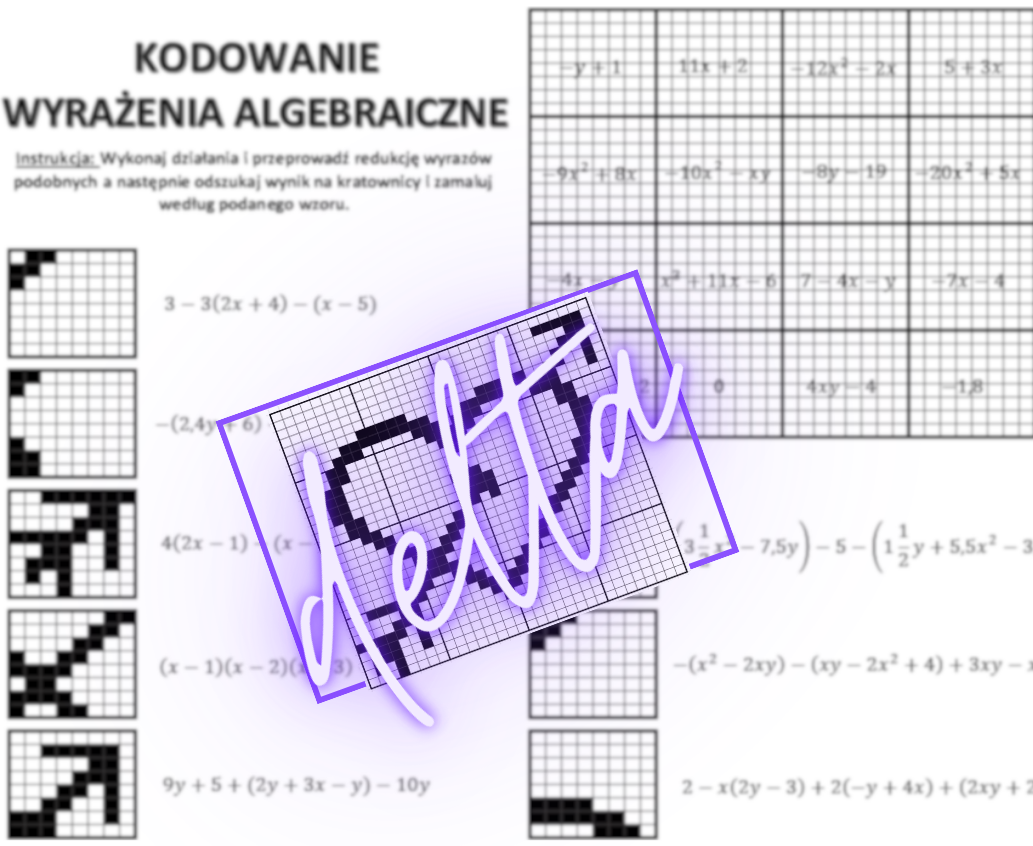
Sprawdzian Z Wyrazen Algebraicznych Kl 7

Pamiętam doskonale, jak na lekcjach matematyki w siódmej klasie, kiedy pojawiły się wyrażenia algebraiczne, w powietrzu unosiło się pewne napięcie. Nauczyciele zmagali się z tłumaczeniem abstrakcyjnych koncepcji, a uczniowie często czuli się zagubieni, jakby nagle przenieśli się do innego świata, gdzie litery zaczęły zastępować liczby, a znane zasady zdawały się ulegać nieuchwytnym zmianom. Rodzice z kolei, widząc swoje pociechy zmagające się z zadaniami, sami zaczynali wątpić w swoje matematyczne umiejętności, pamiętając własne trudności z algebrą. To moment, w którym wspólne wysiłki – nauczycieli, uczniów i rodziców – są kluczowe, aby przebrnąć przez ten etap z sukcesem.

Wielu z nas ma w pamięci ten specyficzny moment w edukacji, kiedy matematyka staje się mniej konkretna, a bardziej abstrakcyjna. Wyrażenia algebraiczne, z ich literami i symbolami, mogą być dla siódmoklasistów jak zaszyfrowana wiadomość. Zrozumiałe jest więc, że sprawdzian z tego zakresu budzi pewne obawy. To naturalne, że czasami czujemy się przytłoczeni nowymi zagadnieniami, szczególnie gdy wydają się tak odległe od codziennego życia.

Przezwyciężanie lęku przed algebrą: Co czeka nas na sprawdzianie?

Sprawdzian z wyrażeń algebraicznych w siódmej klasie to zazwyczaj moment podsumowania wiedzy zdobytej w pierwszych miesiącach nauki tego działu. Nie należy go postrzegać jako narzędzie wyłącznie do oceniania, ale przede wszystkim jako szansę na sprawdzenie swoich postępów i zidentyfikowanie obszarów, które wymagają dalszej pracy. Zamiast paniki, proponuję podejście strategiczne.

Czego możemy się spodziewać? Przede wszystkim zadań związanych z zapisywaniem wyrażeń algebraicznych na podstawie opisów słownych. Na przykład, jeśli nauczycielka mówi: "Suma dwóch liczb, gdzie jedna jest o 5 większa od drugiej", oczekuje się, że uczeń zapisze to jako x + (x + 5) lub 2x + 5. To pierwszy i fundamentalny krok – przekładanie języka polskiego na język matematyki.

Kolejnym ważnym elementem są upraszczanie wyrażeń algebraicznych. Dotyczy to łączenia wyrazów podobnych. Jeśli mamy 3a + 5b - a + 2b, celem jest sprowadzenie tego do prostszej formy, czyli 2a + 7b. Nauczyciele często podkreślają, że to jak porządkowanie pokoju – grupujemy rzeczy tego samego typu.

Nie ominą nas zapewne zadania polegające na obliczaniu wartości wyrażeń algebraicznych dla podanych wartości zmiennych. To tutaj widzimy, jak algebra zaczyna nabierać konkretnego wymiaru. Jeśli mamy wyrażenie 2x - 3y, a wiemy, że x = 4 i y = 1, podstawiamy te wartości i otrzymujemy 2*4 - 3*1 = 8 - 3 = 5. To moment, w którym abstrakcja ustępuje miejsca konkretnemu wynikowi.

Często pojawiają się również zadania z usuwaniem nawiasów, uwzględniające znaki "+" i "-" przed nawiasami. Na przykład, (2a + 3b) - (a - b) wymaga uwagi przy zmianie znaków w drugim nawiasie, co prowadzi do 2a + 3b - a + b = a + 4b. To zadanie uczy precyzji i skupienia.

Warto też wspomnieć o wielomianach – wyrażeniach algebraicznych składających się z sumy lub różnicy jednomianów. Na sprawdzianie mogą pojawić się zadania dotyczące ich dodawania i odejmowania, co jest naturalną konsekwencją umiejętności upraszczania i łączenia wyrazów podobnych.

Dlaczego algebra jest ważna? Praktyczne zastosowania w codziennym życiu

Jednym z najczęstszych pytań, jakie słyszę od uczniów, jest: "Po co mi to?". To pytanie zasługuje na poważną odpowiedź. Algebra, choć na pierwszy rzut oka abstrakcyjna, jest fundamentem wielu dziedzin nauki i techniki, a jej zasady przenikają do naszego codziennego życia w sposób, którego często nie dostrzegamy.

Wyobraźmy sobie planowanie budżetu. Kiedy chcemy obliczyć, ile pieniędzy nam zostanie po wydaniu określonej kwoty, możemy użyć prostego wyrażenia algebraicznego. Jeśli mamy P złotych i wydamy W złotych, to pozostała kwota to P - W. Jeśli chcemy kupić n przedmiotów po cenie c każdy, to całkowity koszt wynosi n * c. Algebra pozwala nam modelować i rozwiązywać problemy w sposób systematyczny.

Rozważmy przykład z gotowania. Przepis na ciasto jest dla 6 osób, ale chcemy przygotować je dla 12. Musimy podwoić wszystkie składniki. Jeśli oryginalny przepis wymaga m gramów mąki, to dla podwojonej liczby osób potrzebujemy 2m gramów. To właśnie algebra w praktyce!

W świecie technologii, od tworzenia aplikacji mobilnych po projektowanie stron internetowych, algebra jest niezbędna do tworzenia algorytmów i rozwiązywania problemów logicznych. Gracze komputerowi, nawet nieświadomie, korzystają z praw algebry, gdy ich ulubiona gra optymalizuje grafikę czy oblicza trajektorię pocisku.

Badania wskazują, że umiejętność logicznego myślenia, rozwijana między innymi dzięki nauce algebry, jest kluczowa dla sukcesu w wielu zawodach, nie tylko tych ściśle związanych z naukami ścisłymi. Analiza danych, rozwiązywanie problemów, kreatywne myślenie – to wszystko opiera się na zdolnościach, które algebra pomaga kształtować.

Według raportów edukacyjnych, uczniowie, którzy dobrze radzą sobie z matematyką, często wykazują lepsze wyniki w innych przedmiotach, co sugeruje, że matematyczne myślenie wpływa na ogólną sprawność intelektualną.

Jak skutecznie przygotować się do sprawdzianu? Strategie dla uczniów i rodziców

Przygotowanie do sprawdzianu z wyrażeń algebraicznych nie musi być stresujące. Kluczem jest systematyczność i odpowiednie metody nauki.

Dla uczniów:

• Powtórz podstawy: Upewnij się, że rozumiesz definicje wyrazu algebraicznego, jednomianu, dwumianu, wielomianu, a także pojęcia takie jak współczynnik i zmienna.
• Ćwicz, ćwicz i jeszcze raz ćwicz: Najlepszym sposobem na opanowanie algebry jest rozwiązywanie jak największej liczby zadań. Zacznij od prostszych przykładów, stopniowo przechodząc do trudniejszych.
• Rozłóż problem na czynniki: Jeśli zadanie wydaje się skomplikowane, spróbuj podzielić je na mniejsze, łatwiejsze do rozwiązania kroki.
• Zrozum błędy: Nie zniechęcaj się błędami. Analizuj, gdzie popełniłeś pomyłkę i staraj się zrozumieć przyczynę. Często to właśnie przez błędy uczymy się najwięcej.
• Wykorzystaj materiały dostępne online: Istnieje wiele darmowych zasobów edukacyjnych, filmów instruktażowych i interaktywnych ćwiczeń, które mogą pomóc w nauce.
• Pracuj z kolegami: Uczenie się w grupie może być bardzo efektywne. Tłumaczenie materiału innym utrwala twoją własną wiedzę.

Dla rodziców:

• Stwórz spokojną atmosferę do nauki: Zapewnij dziecku ciche i komfortowe miejsce do odrabiania lekcji i powtórek.
• Bądź cierpliwy i wyrozumiały: Pamiętaj, że siódma klasa to trudny okres. Unikaj presji i krytyki. Zamiast tego, oferuj wsparcie.
• Nie bój się prosić o pomoc: Jeśli widzisz, że dziecko ma duże trudności, warto rozważyć lekcje z korepetytorem lub dodatkowe konsultacje z nauczycielem.
• Zachęcaj do zadawania pytań: Podkreślaj, że zadawanie pytań jest oznaką inteligencji, a nie niewiedzy.
• Połącz matematykę z życiem codziennym: Pokazuj dziecku, jak algebra jest obecna w otaczającym nas świecie. Wspólne rozwiązywanie prostych problemów matematycznych może być świetną zabawą.
• Celebruj małe sukcesy: Doceniaj postępy dziecka, nawet te najmniejsze. Pozytywne wzmocnienie jest bardzo motywujące.

Pamiętajmy, że sprawdzian z wyrażeń algebraicznych to tylko jeden z etapów nauki. Ważniejsze od samej oceny jest zrozumienie materiału i rozwinięcie umiejętności logicznego myślenia. Z odpowiednim przygotowaniem i wsparciem, nawet najbardziej skomplikowane wyrażenia algebraiczne staną się dla siódmoklasistów czymś więcej niż tylko literami i liczbami – staną się narzędziem do rozumienia świata.

Mam nadzieję, że ten tekst dostarczył Wam cennych wskazówek i pokazał, że algebra nie musi być straszna. Powodzenia na sprawdzianie!