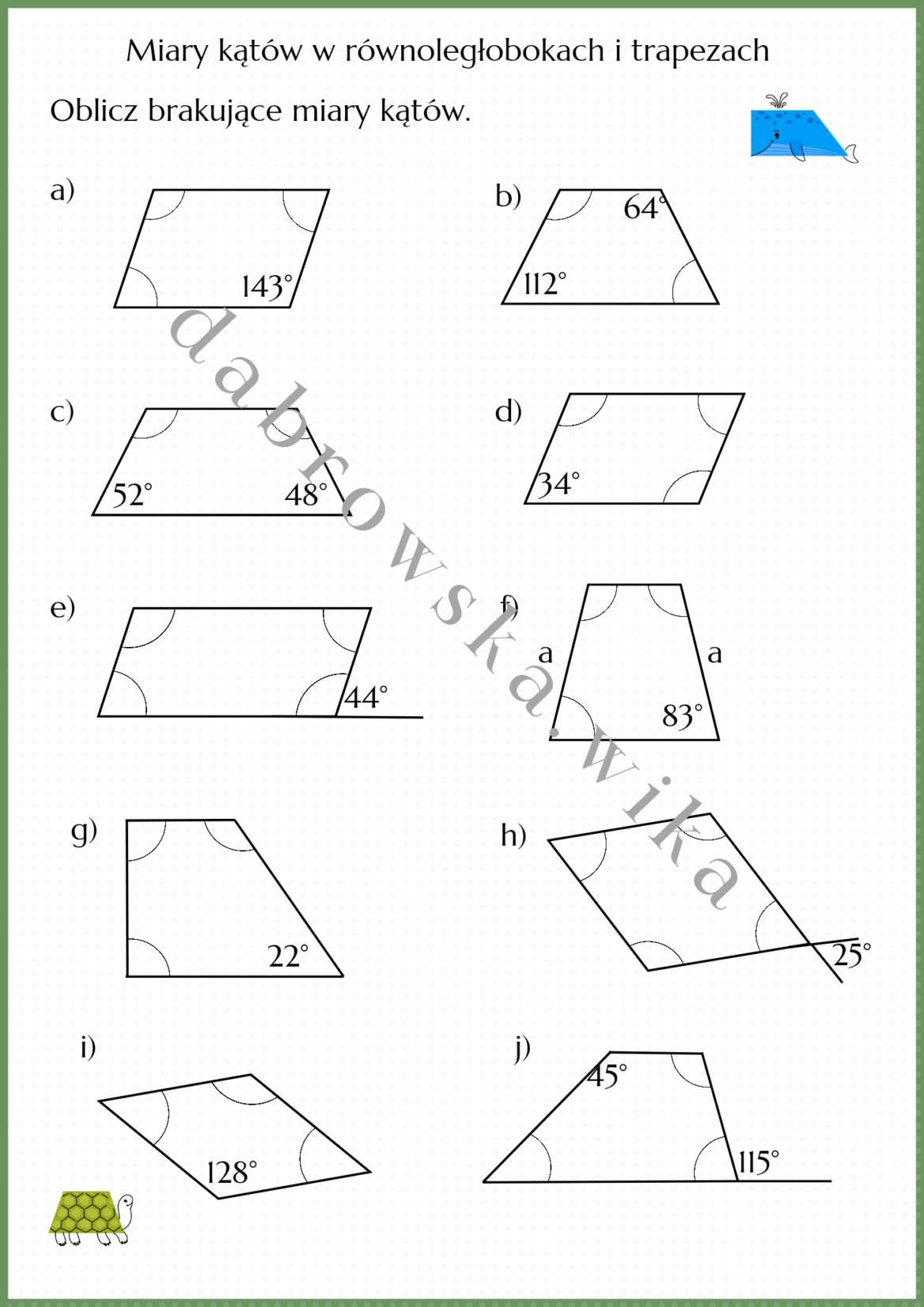
Sprawdzian Z Kątów W Czworokątach Klasa 6

Czy Twoje dziecko z niepokojem spogląda na zbliżający się sprawdzian z kątów w czworokątach? Rozumiemy to doskonale! Matematyka, zwłaszcza w tej fazie nauki, może wydawać się skomplikowana, a figury geometryczne, z ich specyficznymi nazwami i własnościami, bywają wyzwaniem. Szczególnie kąty, ich miary i zależności, potrafią sprawić, że nawet najbystrzejszy uczeń poczuje się zagubiony. Nie martwcie się jednak – jesteście w dobrym miejscu. Ten artykuł powstał właśnie po to, by Was wesprzeć, rozwiać wątpliwości i pokazać, że matematyka może być przyjazna i zrozumiała.

W klasie szóstej uczniowie poznają podstawowe pojęcia dotyczące figur geometrycznych, w tym czworokątów. To kluczowy moment, w którym budowane są fundamenty pod bardziej zaawansowane zagadnienia. Zrozumienie własności kątów w czworokątach to nie tylko kwestia zaliczenia sprawdzianu, ale także rozwijanie logicznego myślenia i umiejętności rozwiązywania problemów, które są nieocenione w wielu dziedzinach życia. Dlatego warto podejść do tematu z ciekawością i spokojem.

Dlaczego kąty w czworokątach sprawiają trudność?

Główne wyzwania związane z kątami w czworokątach często wynikają z kilku czynników. Po pierwsze, bogactwo nazw: trapez, równoległobok, romb, prostokąt, kwadrat – każde z tych słów ma swoje konkretne znaczenie i powiązane z nim właściwości kątowe. Po drugie, konieczność zapamiętania wzorów i twierdzeń. Choć na tym etapie są to podstawowe zależności, to jednak ich właściwe zastosowanie wymaga wprawy.

Po trzecie, wizualizacja. Nie zawsze łatwo jest od razu zobaczyć, które kąty są sobie równe, które sumują się do danej wartości, czy jakie relacje łączą kąty wewnętrzne z zewnętrznymi. Szczególnie w przypadku figur, które nie są "idealne" jak kwadrat czy prostokąt, potrzeba chwili, by odnaleźć potrzebne zależności.

Badania dotyczące nauczania matematyki często wskazują, że "próg wejścia" do geometrii bywa dla wielu uczniów wyższy niż do algebry. Wynika to z potrzeby operowania na obiektach wizualnych i abstrakcyjnych jednocześnie. Jak mówi znany pedagog i matematyk, prof. Maria Stern: "Geometria uczy nas nie tylko mierzyć i rysować, ale przede wszystkim patrzeć i myśleć przestrzennie. To umiejętność, którą często niedoceniamy, a która jest kluczowa dla rozwoju intelektualnego."

Kluczowe pojęcia, które musisz znać

Zanim przejdziemy do strategii rozwiązywania zadań, przypomnijmy sobie podstawowe definicje i własności, które są niezbędne do zrozumienia kątów w czworokątach.

1. Suma kątów wewnętrznych w każdym czworokącie

To jest absolutna podstawa. Niezależnie od tego, jak wygląda czworokąt – czy jest to równoległobok, trapez, czy zupełnie nieregularna figura – suma jego kątów wewnętrznych zawsze wynosi 360 stopni. To jest jak matematyczna "złota zasada" dla czworokątów.

Dlaczego tak jest? Możemy to łatwo udowodnić, dzieląc dowolny czworokąt na dwa trójkąty za pomocą przekątnej. Wiemy, że suma kątów w każdym trójkącie to 180 stopni. Skoro mamy dwa takie trójkąty, to ich połączona suma kątów daje 180 + 180 = 360 stopni.

2. Specjalne rodzaje czworokątów i ich kąty

Każdy z tych czworokątów ma swoje unikalne właściwości kątowe, które warto zapamiętać:

• Prostokąt: Wszystkie cztery kąty są proste, czyli mają miarę 90 stopni. Dwa pary przeciwległych boków są równe.
• Kwadrat: Jest to szczególny przypadek prostokąta (i rombu). Wszystkie cztery kąty mają miarę 90 stopni, a wszystkie boki są równe.
• Równoległobok: Kąty leżące naprzeciwko siebie są równe. Kąty leżące przy tym samym boku (sąsiednie) sumują się do 180 stopni. Dwa pary przeciwległych boków są równoległe i równe.
• Trapez: To czworokąt, który ma co najmniej jedną parę boków równoległych. W zależności od rodzaju trapezu mamy dodatkowe własności:
  • Trapez równoramienny: Kąty przy tej samej podstawie są równe.
  • Trapez prostokątny: Ma co najmniej jeden kąt prosty.

Kluczem jest zrozumienie, że kwadrat i prostokąt to też równoległoboki (choć bardzo szczególne), a kwadrat to też prostokąt. Wiedza o tych relacjach pomaga unikać błędów.

Jak skutecznie przygotować się do sprawdzianu?

Nie dajcie się przytłoczyć! Dobra strategia przygotowań to już połowa sukcesu. Oto kilka praktycznych wskazówek, które pomogą Twojemu dziecku opanować materiał:

1. Wizualizuj, rysuj, mierz!

Geometria jest nauką wizualną. Zachęcaj dziecko do rysowania czworokątów – nie tylko tych "idealnych". Niech używa linijki i kątomierza. Nawet jeśli rysunek nie jest idealny, pomaga to zrozumieć kształt i położenie kątów. Możecie nawet sami tworzyć zadania, rysując czworokąt i wpisując miary kilku kątów, a potem prosić o obliczenie brakujących.

Przykład: Narysuj równoległobok. Wpisz miarę jednego kąta, np. 70 stopni. Jakie są miary pozostałych kątów? Jeśli jeden kąt to 70 stopni, to kąt naprzeciwko niego również ma 70 stopni. Kąty leżące przy tym samym boku to 180 - 70 = 110 stopni. Czyli mamy dwa kąty po 70 stopni i dwa po 110 stopni. Suma: 70+70+110+110 = 360 stopni. Zawsze sprawdzajcie sumę!

2. Rozbijaj zadania na mniejsze kroki

Gdy dziecko widzi zadanie, zamiast panikować, powinno nauczyć się je analizować:

• Jaki to czworokąt? Czy ma jakąś specjalną nazwę (prostokąt, trapez itp.)?
• Co wiemy o kątach tego czworokąta? Jakie są jego własności?
• Jakie są dane w zadaniu? Jakie miary kątów już znamy?
• Czego szukamy? Jaką miarę kąta mamy obliczyć?
• Jaką zasadę lub wzór można zastosować?

To systematyczne podejście pozwala na uniknięcie błędów i pewniejsze dojście do prawidłowego wyniku.

3. Ćwicz, ćwicz i jeszcze raz ćwicz!

Nie ma lepszego sposobu na utrwalenie wiedzy niż regularne ćwiczenia. Powtarzajcie zadania o różnym stopniu trudności. Zacznijcie od prostych przykładów, gdzie wystarczy zastosować jedną własność (np. suma kątów w czworokącie), a potem przechodźcie do bardziej złożonych, gdzie trzeba połączyć kilka zasad.

Istnieje wiele zasobów: podręczniki, zeszyty ćwiczeń, strony internetowe z zadaniami matematycznymi dla klas 6. Warto korzystać z różnorodnych materiałów, aby dziecko miało kontakt z różnymi sposobami formułowania zadań.

4. Zrozumienie, nie tylko pamięć

Choć zapamiętanie własności jest ważne, to kluczem jest zrozumienie, dlaczego te własności działają. Jeśli dziecko rozumie, skąd bierze się suma 360 stopni, lub dlaczego kąty przy podstawie trapezu równoramiennego są równe, to zadania stają się logiczne, a nie tylko mechaniczne.

Zachęcaj dziecko do wyjaśniania, jak rozwiązało dane zadanie. Tłumaczenie komuś (nawet sobie samemu) procesu myślowego jest jednym z najskuteczniejszych sposobów na upewnienie się, że materiał został dobrze przyswojony.

5. Skup się na typowych zadaniach ze sprawdzianów

Jeśli masz dostęp do przykładowych sprawdzianów lub zadań, które mogą pojawić się na lekcji, przeróbcie je wspólnie. Zwróćcie uwagę na powtarzające się typy zadań i sposoby ich rozwiązywania. To pomoże zminimalizować stres związany z nieznanym formatem pytań.

Przykładowe zadania i ich rozwiązania

Przyjrzyjmy się kilku typowym zadaniom, które mogą pojawić się na sprawdzianie, i sposobom ich rozwiązywania.

Zadanie 1: Obliczanie brakującego kąta w nieregularnym czworokącie

Treść: W czworokącie ABCD podano miary trzech kątów: Kąt A = 80°, Kąt B = 100°, Kąt C = 110°. Oblicz miarę kąta D.

Rozwiązanie: Wiemy, że suma kątów wewnętrznych w każdym czworokącie wynosi 360°. Zatem: Kąt A + Kąt B + Kąt C + Kąt D = 360°. Podstawiamy dane: 80° + 100° + 110° + Kąt D = 360°. Sumujemy znane kąty: 290° + Kąt D = 360°. Obliczamy Kąt D: Kąt D = 360° - 290° = 70°.

Zadanie 2: Kąty w równoległoboku

Treść: Jeden z kątów równoległoboku ma miarę 55°. Oblicz miary pozostałych kątów tego równoległoboku.

Rozwiązanie: W równoległoboku kąty naprzeciwległe są równe, a kąty leżące przy tym samym boku sumują się do 180°. Jeśli jeden kąt ma 55°, to kąt naprzeciwko niego również ma 55°. Kąty leżące przy tym samym boku wynoszą: 180° - 55° = 125°. Kąt naprzeciwko tego kąta również ma 125°. Sprawdzenie: 55° + 125° + 55° + 125° = 360°. Odpowiedź: Pozostałe kąty to 55°, 125°, 125°.

Zadanie 3: Kąty w trapezie równoramiennym

Treść: W trapezie równoramiennym miara jednego z kątów przy dłuższej podstawie wynosi 65°. Oblicz miary pozostałych kątów.

Rozwiązanie: W trapezie równoramiennym kąty przy tej samej podstawie są równe. Oznacza to, że oba kąty przy dłuższej podstawie mają po 65°. Suma kątów przy krótszej podstawie musi być taka, aby suma wszystkich kątów wynosiła 360°. Ponieważ dłuższa i krótsza podstawa są równoległe, to kąty leżące przy ramieniu (czyli jeden kąt przy dłuższej podstawie i jeden kąt przy krótszej podstawie) sumują się do 180°. Zatem kąty przy krótszej podstawie mają miarę: 180° - 65° = 115°. Ponieważ jest to trapez równoramienny, te dwa kąty również są równe. Sprawdzenie: 65° + 65° + 115° + 115° = 360°. Odpowiedź: Pozostałe kąty to 65°, 115°, 115°.

Wsparcie i pozytywne nastawienie

Pamiętajcie, że okres przygotowań do sprawdzianu to również doskonała okazja do wspólnego spędzania czasu i budowania pewności siebie u dziecka. Nie naciskajcie za mocno, ale bądźcie obecni i gotowi do pomocy. Chwalcie za wysiłek i postępy, nawet te małe.

Jeśli widzicie, że dziecko naprawdę się męczy i nie radzi sobie z materiałem, warto rozważyć dodatkowe korepetycje lub poprosić o pomoc nauczyciela. Czasem wystarczy jedno dodatkowe wyjaśnienie, aby "zapaliło się światełko" i trudny temat stał się zrozumiały.

Na koniec, podejdźcie do sprawdzianu z pozytywnym nastawieniem. Powiedzcie dziecku, że jesteście z niego dumni za to, jak bardzo się stara. Sukces to nie tylko wynik, ale przede wszystkim proces nauki i pokonywania własnych trudności.

Życzymy Wam wszystkim powodzenia i samych sukcesów na sprawdzianie! Pamiętajcie – matematyka wcale nie musi być straszna. Wystarczy podejść do niej z odpowiednią strategią i odrobiną cierpliwości.