Sprawdzian Z Graniastosłupów 3 Gimnazjum
Sprawdzian z graniastosłupów dla klasy 3 gimnazjum sprawdza zrozumienie podstawowych pojęć związanych z tymi bryłami, umiejętność obliczania ich pól powierzchni i objętości oraz rozpoznawania różnych typów graniastosłupów.
Podstawowa definicja graniastosłupa: Jest to bryła geometryczna ograniczona dwiema wielokątnymi podstawami, które są przystające i równoległe, oraz ścianami bocznymi, które są równoległobokami. Graniastosłup, w którym ściany boczne są prostopadłe do podstaw, nazywamy graniastosłupem prostym.
Kluczowe aspekty sprawdzianu:
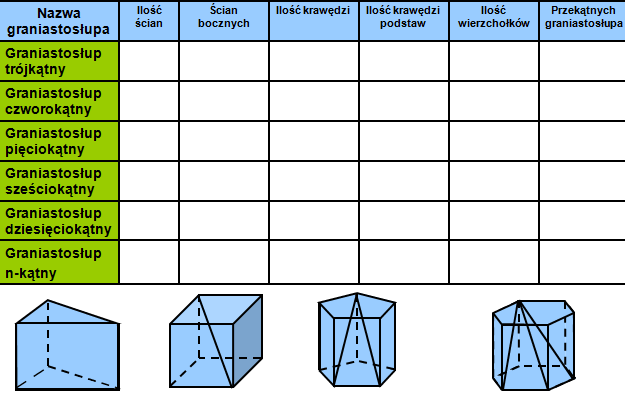
1. Rodzaje graniastosłupów: Sprawdzian często wymaga rozpoznania i nazwania graniastosłupów na podstawie kształtu ich podstaw. Najczęściej spotykane to:
- Graniastosłup trójkątny (podstawa to trójkąt)
- Graniastosłup czworokątny (podstawa to czworokąt)
- Graniastosłup sześciokątny (podstawa to sześciokąt)
Szczególnym przypadkiem graniastosłupa czworokątnego prostego jest prostopadłościan, a jego szczególnym przypadkiem jest sześcian (wszystkie ściany kwadratowe).
2. Pole powierzchni całkowitej: Jest to suma pól wszystkich ścian graniastosłupa. Oblicza się je, sumując pola dwóch podstaw i pól wszystkich ścian bocznych. Wzór ogólny dla graniastosłupa prostego to: P_c = 2 * P_p + P_b, gdzie P_c to pole powierzchni całkowitej, P_p to pole jednej podstawy, a P_b to pole powierzchni bocznej.
3. Pole powierzchni bocznej: Jest to suma pól wszystkich ścian bocznych. Dla graniastosłupa prostego, pole powierzchni bocznej można obliczyć jako iloczyn obwodu podstawy i wysokości graniastosłupa: P_b = O_p * h, gdzie O_p to obwód podstawy, a h to wysokość graniastosłupa.
4. Objętość: Jest to miara przestrzeni zajmowanej przez bryłę. Wzór na objętość graniastosłupa prostego jest prosty: V = P_p * h, gdzie V to objętość, P_p to pole jednej podstawy, a h to wysokość graniastosłupa.
Przykłady:
Przykład 1: Oblicz objętość graniastosłupa prostego, którego podstawą jest kwadrat o boku 4 cm, a wysokość graniastosłupa wynosi 10 cm.
Rozwiązanie: Pole podstawy P_p = 4 cm * 4 cm = 16 cm². Objętość V = 16 cm² * 10 cm = 160 cm³.
Przykład 2: Oblicz pole powierzchni całkowitej graniastosłupa trójkątnego prostego, którego podstawą jest trójkąt równoboczny o boku 6 cm, a wysokość graniastosłupa wynosi 8 cm.
Rozwiązanie: Pole podstawy trójkąta równobocznego P_p = (a²√3)/4 = (6²√3)/4 = 9√3 cm². Obwód podstawy O_p = 3 * 6 cm = 18 cm. Pole powierzchni bocznej P_b = 18 cm * 8 cm = 144 cm². Pole powierzchni całkowitej P_c = 2 * 9√3 cm² + 144 cm² = 18√3 + 144 cm².
Zastosowanie w życiu codziennym:
Graniastosłupy są wszechobecne. Pudełka, cegły, budynki (często mają kształt prostopadłościanów lub bardziej złożonych graniastosłupów), stoły – to wszystko przykłady przedmiotów o kształtach graniastosłupów. Zrozumienie ich właściwości pozwala na dokładne planowanie przestrzeni, obliczanie potrzebnych materiałów (np. farby do pomalowania ścian, pojemności opakowań) oraz rozwiązywanie problemów konstrukcyjnych.






