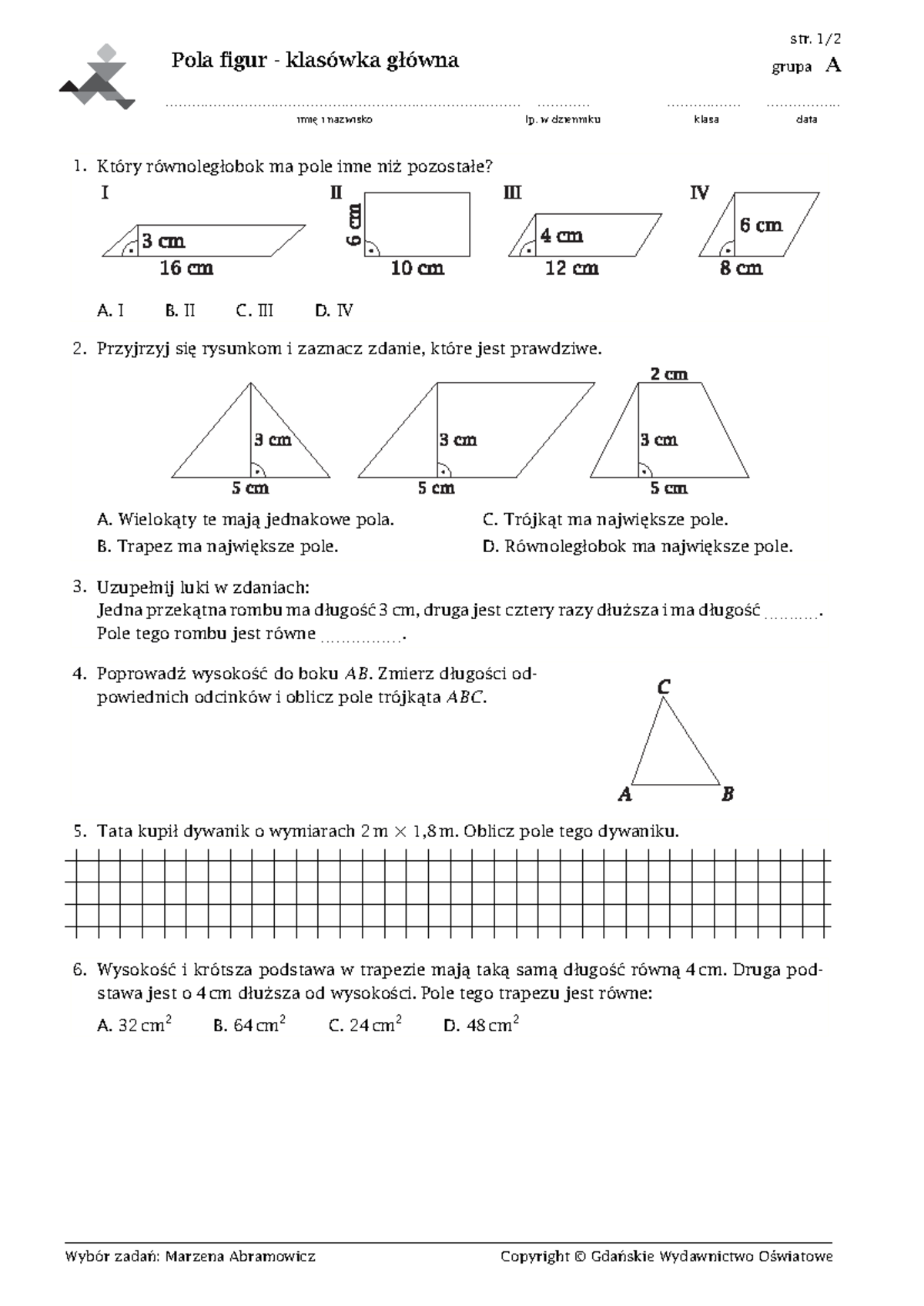
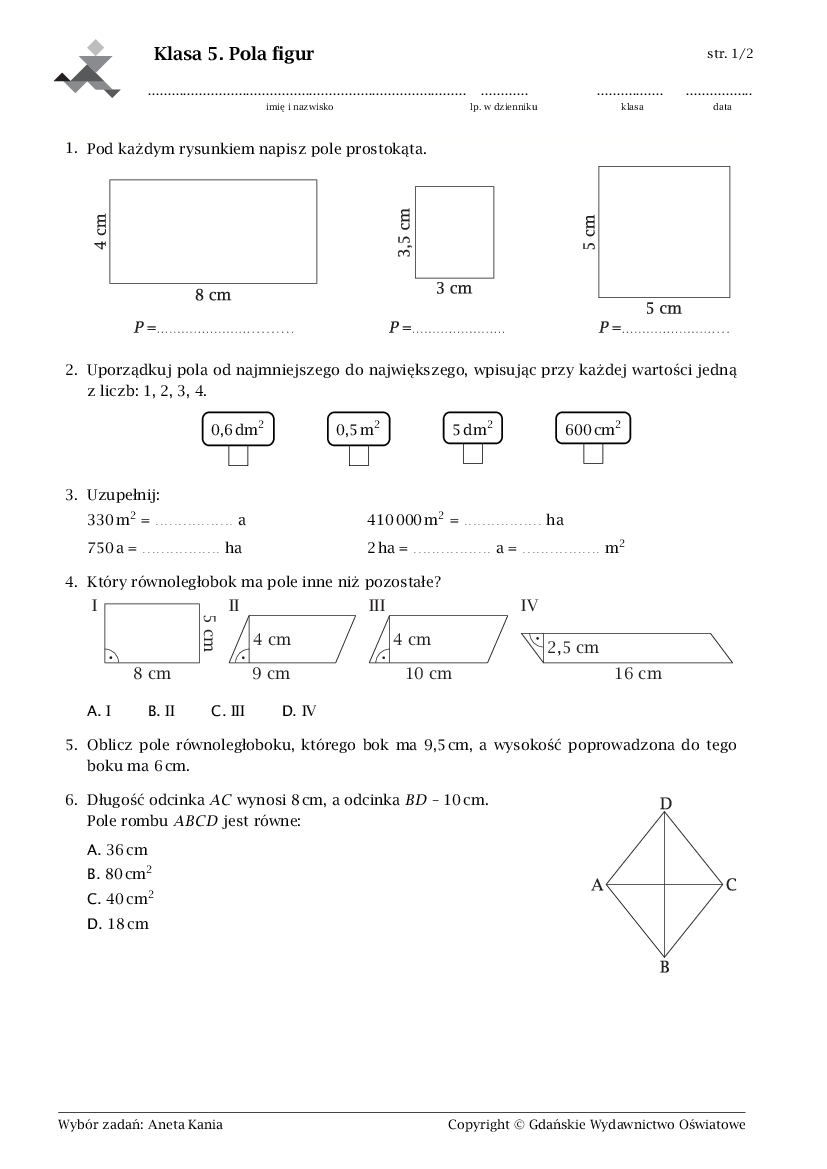
Sprawdzian Z Geometrii Klasa 6 Pola Figur

Kształty otaczają nas wszędzie, od prostych przedmiotów codziennego użytku po skomplikowane konstrukcje architektoniczne. Zrozumienie ich wymiarów i przestrzeni, jaką zajmują, jest fundamentalnym elementem nauki, a w szczególności matematyki. W szóstej klasie szkoły podstawowej uczniowie stykają się z pojęciem pola figur, które stanowi klucz do analizy i opisu tych geometrycznych obiektów. Pola figur to miara dwuwymiarowej przestrzeni zajmowanej przez płaską figurę geometryczną. Określa ona, ile jednostek kwadratowych (np. centymetrów kwadratowych, metrów kwadratowych) mieści się wewnątrz obwodu danej figury. Jest to pojęcie o ogromnym znaczeniu edukacyjnym, które kształtuje logiczne myślenie i umiejętność rozwiązywania problemów.

Dlaczego Pola Figur są Ważne dla Ucznia Klasy 6?

Nauka o polach figur w szóstej klasie nie jest jedynie abstrakcyjnym ćwiczeniem matematycznym. Jest to etap, na którym uczniowie zaczynają dostrzegać praktyczne zastosowania matematyki w realnym świecie. Zrozumienie, jak obliczyć pole prostokąta, kwadratu, trójkąta czy równoległoboku, buduje fundamenty pod bardziej zaawansowane zagadnienia geometryczne i algebraiczne w przyszłości. Ignorowanie tego tematu lub jego powierzchowne opanowanie może prowadzić do trudności w dalszej edukacji, zwłaszcza w przedmiotach takich jak fizyka, technika, a nawet informatyka, gdzie modele przestrzenne i ich parametry są kluczowe.

Eksperci podkreślają rolę wczesnego kontaktu z praktycznymi aspektami matematyki. Jak zauważa dr hab. Maria Kwiatkowska, specjalistka od dydaktyki matematyki, "Zastosowanie teorii w praktyce, nawet na najprostszych przykładach, buduje w uczniach poczucie sensu nauki i motywuje do dalszego zgłębiania wiedzy. Pola figur stanowią doskonały przykład takiej praktycznej aplikacji matematyki dla uczniów szkoły podstawowej". Zrozumienie pojęcia pola pozwala uczniom na konceptualizację przestrzeni i rozwijanie intuicji geometrycznej. Umożliwia analizę wielkości i porównywanie różnych kształtów pod względem zajmowanej przez nie przestrzeni.

Kluczowe Figury i Ich Obliczanie

W szóstej klasie uczniowie zazwyczaj skupiają się na obliczaniu pól kilku podstawowych figur. Każda z nich wymaga specyficznego podejścia i wzoru.

Prostokąt i Kwadrat

Prostokąt, figura o czterech kątach prostych i przeciwległych bokach równej długości, jest jedną z pierwszych figur, dla których uczniowie poznają wzór na pole. Oblicza się je mnożąc długość jednego boku przez długość boku sąsiedniego: P = a * b, gdzie 'a' i 'b' to długości boków. Kwadrat, będący szczególnym przypadkiem prostokąta, gdzie wszystkie boki są równej długości ('a'), ma analogiczny wzór: P = a * a, czyli P = a². Uczniowie często budują swój pierwszy intuicyjny model pola właśnie na przykładzie kwadratu, układając na jego powierzchni mniejsze, jednostkowe kwadraciki.

Trójkąt

Obliczanie pola trójkąta jest nieco bardziej złożone. Podstawowy wzór to P = (1/2) * a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę. Zrozumienie pojęcia wysokości, która może znajdować się zarówno wewnątrz trójkąta, jak i poza nim (w przypadku trójkątów rozwartokątnych), jest kluczowe dla poprawnego zastosowania wzoru. Uczniowie często doświadczają tej zależności, dzieląc prostokąt lub równoległobok po przekątnej, co pokazuje, że każdy z powstałych trójkątów ma połowę pola pierwotnej figury.

Równoległobok

Pole równoległoboku oblicza się również za pomocą wzoru P = a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę. Równoległobok można przekształcić w prostokąt o tym samym polu, co stanowi ważną wizualizację matematyczną, którą uczniowie mogą odkryć podczas lekcji. Odcięcie trójkąta z jednej strony i przeniesienie go na drugą stronę figury tworzy prostokąt.

Praktyczne Zastosowania w Szkole i Życiu Codziennym

Umiejętność obliczania pól figur jest niezwykle praktyczna i znajduje zastosowanie w wielu aspektach życia.

Majsterkowanie i DIY: Kiedy uczeń chce samodzielnie pomalować ścianę swojego pokoju, musi wiedzieć, jaką powierzchnię ma ściana, aby oszacować ilość potrzebnej farby. Podobnie, planując ułożenie płytek w łazience lub wycięcie elementu z drewna, konieczne jest precyzyjne obliczenie pola.
Ogrodnictwo: Planowanie ogródka, rozsiewanie nasion czy układanie trawnika wymaga wiedzy o polu powierzchni, którą chcemy zagospodarować. Ile nawozu potrzebujemy na metr kwadratowy rabatki? To pytanie, na które odpowiedź można znaleźć dzięki znajomości geometrii.
Projektowanie i Architektura: Nawet na podstawowym poziomie, dzieci mogą projektować własne pokoje czy domki na drzewie, starając się oszacować, ile materiału potrzebują na podłogę czy dach. To pierwsze kroki w kierunku myślenia projektowego i inżynieryjnego.
Gry i Zabawy: Wiele gier planszowych, łamigłówek geometrycznych czy nawet gier wideo opiera się na koncepcjach przestrzennych i obliczeniach powierzchni. Dzieci naturalnie bawią się, porównując wielkości i kształty, a matematyka dostarcza narzędzi do formalizacji tych obserwacji.

Zajęcia związane z obliczaniem pól często wykorzystują materiały manipulacyjne i wizualizacje. Jak podkreśla prof. Janusz Kowalski, ceniony dydaktyk matematyki: "Kiedy uczniowie mogą fizycznie układać jednostkowe kwadraty na powierzchni figury, czy też samodzielnie przekształcać równoległobok w prostokąt, proces uczenia się staje się bardziej angażujący i zrozumiały. Matematyka powinna być doświadczeniem, a nie tylko zapamiętywaniem wzorów".

Wyzwania i Jak Sobie z Nimi Radzić

Pomimo praktycznego charakteru, temat pól figur może stanowić wyzwanie dla niektórych uczniów. Trudności mogą pojawić się przy:

Zrozumieniu abstrakcyjnych wzorów: Niektórzy uczniowie mogą mieć problem z zapamiętaniem i stosowaniem wzorów bez głębszego zrozumienia ich pochodzenia.
Poprawnym identyfikowaniu podstawy i wysokości: Szczególnie w przypadku trójkątów i równoległoboków, znalezienie właściwej wysokości i podstawy bywa kłopotliwe.
Przeliczaniu jednostek: Konieczność pracy z różnymi jednostkami miary (np. centymetry, metry) i ich konwersji może sprawiać trudność.

Aby sprostać tym wyzwaniom, nauczyciele często stosują różnorodne metody nauczania:

Wizualizacje i modele: Użycie materiałów takich jak klocki, papier milimetrowy czy programy komputerowe do tworzenia i analizowania figur.
Kontekstualizacja zadań: Prezentowanie problemów matematycznych w postaci realnych scenariuszy, co zwiększa motywację i ułatwia zrozumienie zastosowań.
Ćwiczenia praktyczne: Zachęcanie uczniów do samodzielnego mierzenia przedmiotów w klasie lub w domu i obliczania ich pól.
Powtarzalność i utrwalenie: Regularne powracanie do zagadnień i rozwiązywanie zróżnicowanych zadań, od prostych po bardziej złożone.

Sprawdzian z pól figur dla szóstej klasy jest ważnym momentem oceny. Nie tylko weryfikuje on, czy uczeń potrafi zastosować odpowiednie wzory, ale także, czy rozumie koncepcję pola jako miary przestrzeni. Jest to kluczowy krok w rozwijaniu kompetencji matematycznych, które będą procentować przez całe życie.