Sprawdzian Z Funkcji Liniowej Liceum Sprwdzian

Drogi Uczniu, Drogi Rodzicu,

Zbliża się sprawdzian z funkcji liniowej. To moment, który dla wielu może budzić pewien niepokój, a nawet stres. Doskonale to rozumiemy. Matematyka, choć fascynująca, bywa czasem postrzegana jako trudna i wymagająca. Chcemy jednak rozwiać wszelkie obawy i pokazać, że funkcja liniowa to nie tylko abstrakcyjne wzory, ale klucz do zrozumienia wielu zjawisk wokół nas. Ten sprawdzian to nie koniec świata, a wręcz przeciwnie – świetna okazja, aby pokazać swoją wiedzę i utrwalić to, co najważniejsze.

Pamiętajmy, że każdy uczeń ma swoje tempo nauki. Niektórzy od razu łapią niuanse, inni potrzebują więcej czasu i powtórek. Ważne jest, aby nie poddawać się i systematycznie pracować. Celem tego artykułu jest nie tylko przygotowanie do sprawdzianu, ale przede wszystkim zbudowanie pewności siebie i pokazanie, że matematyka może być zrozumiała i nawet przyjemna.

Zrozumieć, co to jest funkcja liniowa

Zacznijmy od podstaw. Co tak naprawdę kryje się pod pojęciem funkcji liniowej? Najprościej mówiąc, jest to funkcja, której wykres jest linią prostą. W szkole średniej najczęściej spotykamy się z jej ogólną postacią:

y = ax + b

Gdzie:

• 'a' to współczynnik kierunkowy. On mówi nam, jak "stromo" idzie nasza linia. Jeśli 'a' jest dodatnie, linia idzie w górę. Jeśli ujemne – w dół. A jeśli 'a' wynosi zero? Wtedy mamy do czynienia z funkcją stałą – linia jest równoległa do osi OX.
• 'b' to wyraz wolny, inaczej mówiąc, miejsce, w którym linia przecina oś OY. To bardzo ważny punkt, który często pomaga nam szybko naszkicować wykres.

Dlaczego ta funkcja jest taka ważna? Ponieważ opisuje proste zależności, które widzimy wszędzie. Pomyśl o rachunku za prąd – im więcej zużyjesz kilowatogodzin (x), tym więcej zapłacisz (y). Lub o podróży samochodem – im więcej kilometrów przejedziesz (x), tym więcej paliwa zużyjesz (y), zakładając stałe spalanie. To wszystko są przykłady zależności liniowych!

Nauczyciele często podkreślają, jak istotne jest zrozumienie sensu tych współczynników, a nie tylko wkuwanie wzorów na pamięć. Jak mówi Pani Anna, doświadczona nauczycielka matematyki z liceum: "Kluczem do sukcesu w matematyce jest zadawanie pytań 'dlaczego?'. Dlaczego ten współczynnik jest taki, a nie inny? Co on oznacza w kontekście problemu? Gdy uczniowie zaczną to rozumieć, matematyka przestaje być straszna."

Kluczowe zagadnienia na sprawdzianie

Przygotowując się do sprawdzianu, warto skupić się na kilku fundamentalnych zagadnieniach. Oto one, przedstawione w prosty i uporządkowany sposób:

1. Określanie funkcji i jej własności

Będziesz musiał umieć rozpoznać funkcję liniową spośród innych. To proste – szukaj postaci y = ax + b. Następnie, będziesz analizować współczynnik kierunkowy 'a' (monotoniczność – czy funkcja rośnie, maleje, czy jest stała) i wyraz wolny 'b' (miejsce przecięcia z osią OY).

Ćwiczenie dla Ciebie: Spójrz na listę funkcji:

• f(x) = 2x + 5
• g(x) = -x + 1
• h(x) = 3
• k(x) = x² - 4

2. Wykres funkcji liniowej

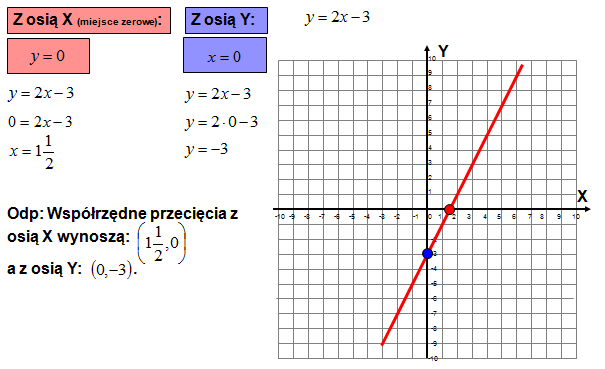
Umiejętność rysowania wykresu funkcji liniowej to podstawa. Najłatwiej to zrobić, znajdując dwa punkty należące do wykresu. Często wybiera się punkty przecięcia z osiami:

• Przecięcie z osią OY: Następuje, gdy x = 0. Wtedy y = b. Zatem punkt ma współrzędne (0, b).
• Przecięcie z osią OX: Następuje, gdy y = 0. Rozwiązujemy równanie ax + b = 0. Wtedy x = -b/a. Zatem punkt ma współrzędne (-b/a, 0).

Praktyczna wskazówka: Zawsze sprawdzaj, czy Twój wykres jest zgodny ze "znakami" współczynników. Rosnąca funkcja (a > 0) powinna iść w górę od lewej do prawej. Funkcja malejąca (a < 0) – w dół. Punkt przecięcia z OY powinien być zgodny z wartością 'b'.

3. Wyznaczanie równania funkcji

Czasem będziesz musiał ustalić równanie funkcji, mając podane pewne informacje. Najczęściej będą to:

• Dwa punkty, przez które przechodzi prosta: Podstawiasz współrzędne tych punktów do wzoru y = ax + b, tworząc układ dwóch równań z dwiema niewiadomymi (a i b).
• Jeden punkt i współczynnik kierunkowy 'a': Podstawiasz współrzędne punktu i podaną wartość 'a' do wzoru y = ax + b i rozwiązujesz dla 'b'.
• Jeden punkt i informacja o równoległości/prostopadłości do innej prostej: To już temat na nieco głębszą analizę, ale kluczowe jest zrozumienie zależności współczynników kierunkowych prostych równoległych (a1 = a2) i prostopadłych (a1 * a2 = -1).

Przykład z życia: Wyobraź sobie, że wiesz, że Twój telefon komórkowy nalicza stałą opłatę miesięczną (np. abonament – to nasze 'b') plus koszt każdej minuty rozmowy (to nasze 'a'). Jeśli wiesz, że w jednym miesiącu (x1 minut) zapłaciłeś Y1 zł, a w innym (x2 minut) Y2 zł, możesz wyznaczyć dokładne równanie funkcji opisującej Twój rachunek! To jest właśnie zastosowanie funkcji liniowej.

4. Rozwiązywanie zadań tekstowych

To często najtrudniejszy element dla uczniów. Kluczem jest uważne czytanie i identyfikacja tego, co jest zmienną (x), co wartością funkcji (y), co współczynnikiem kierunkowym (a) i co wyrazem wolnym (b).

Rada od psychologa szkolnego: "Stres przed sprawdzianem często wynika z obawy przed niewiedzą. Dzieląc materiał na mniejsze części i koncentrując się na jednym zagadnieniu naraz, budujemy poczucie kontroli. Przed rozpoczęciem rozwiązywania zadania tekstowego, poświęć minutę, dwie na zastanowienie się: 'O czym jest to zadanie? Jakie dane mam? Czego szukam?' To już połowa sukcesu."

Przykładowe zadanie tekstowe: Firma kurierska pobiera opłatę początkową za dostarczenie paczki oraz opłatę za każdy przejechany kilometr. Wiadomo, że za dostarczenie paczki na odległość 50 km zapłacono 70 zł, a za dostarczenie na odległość 120 km – 105 zł.

• Wyznacz wzór funkcji liniowej opisującej koszt dostarczenia paczki w zależności od odległości.
• Ile zapłacimy za dostarczenie paczki na odległość 200 km?

• x – to odległość w kilometrach.
• y – to koszt dostarczenia w złotówkach.
• Mamy dwa punkty: (50, 70) i (120, 105).

Jak skutecznie się przygotować?

Skuteczne przygotowanie to nie tylko przeglądanie notatek w ostatniej chwili. To proces, który powinien być systematyczny i przemyślany. Oto kilka sprawdzonych metod:

1. Systematyczność to podstawa

Nie zostawiaj nauki na ostatni wieczór. Lepiej poświęcić 30 minut każdego dnia na powtórkę materiału niż 4 godziny tuż przed sprawdzianem. Rozbij materiał na mniejsze partie i przyswajaj je stopniowo.

2. Rozwiązywanie zadań, zadań i jeszcze raz zadań!

Matematyka to umiejętność praktyczna. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zagadnienia i tym pewniej będziesz czuć się podczas sprawdzianu. Zacznij od tych prostszych, a potem przechodź do trudniejszych. Nie zniechęcaj się błędami – są one naturalnym elementem procesu nauki.

Polecamy: Skorzystaj z podręcznika, zbiorów zadań, a także zasobów online. Istnieje wiele stron internetowych i kanałów YouTube oferujących darmowe lekcje i zadania z funkcji liniowej.

3. Współpraca i dyskusja

Uczcie się razem z kolegami i koleżankami! Tłumaczenie zagadnień innym to najlepszy sposób na utrwalenie własnej wiedzy. Wspólne rozwiązywanie zadań i dyskusje pomagają spojrzeć na problem z różnych perspektyw.

4. Wizualizacja

Rysuj wykresy! Wiele osób lepiej rozumie matematykę, gdy widzi jej graficzne przedstawienie. Nie bój się używać kolorowych flamastrów i tworzyć estetycznych wykresów. To nie tylko pomaga w nauce, ale też sprawia, że proces staje się bardziej angażujący.

5. Pytaj o pomoc

Jeśli czegoś nie rozumiesz, nie wahaj się pytać nauczyciela, kolegi, rodzica. Lepiej wyjaśnić wątpliwości od razu, niż pozwolić im narastać. Nauczyciele są od tego, aby pomagać!

Dzień sprawdzianu – jak sobie poradzić ze stresem?

Dzień sprawdzianu może być stresujący, ale można sobie z tym poradzić. Kilka prostych rad:

• Dobrze się wyśpij: Wypoczęty umysł lepiej funkcjonuje.
• Zjedz śniadanie: Daj mózgowi paliwo do pracy.
• Przyjdź wcześniej: Pozwoli Ci to uspokoić się i zebrać myśli.
• Przeczytaj uważnie polecenia: Upewnij się, że rozumiesz, co masz zrobić.
• Zacznij od zadań, które wydają Ci się najłatwiejsze: Pomoże Ci to zbudować pewność siebie.
• Nie martw się o to, co robią inni: Skup się na swoim zadaniu.
• Jeśli utkniesz, przejdź dalej: Wróć do trudniejszego zadania później, być może po rozwiązaniu innych przypomnisz sobie rozwiązanie.

Pamiętaj, że ten sprawdzian to tylko jeden z etapów Twojej edukacji. Niezależnie od wyniku, najważniejsze jest to, czego się nauczysz i jak będziesz się rozwijać.

Trzymamy za Ciebie kciuki! Jesteś w stanie sprostać temu wyzwaniu. Wystarczy odrobina pracy, systematyczności i wiary we własne siły. Funkcja liniowa może stać się Twoim sprzymierzeńcem, a nie wrogiem. Powodzenia!