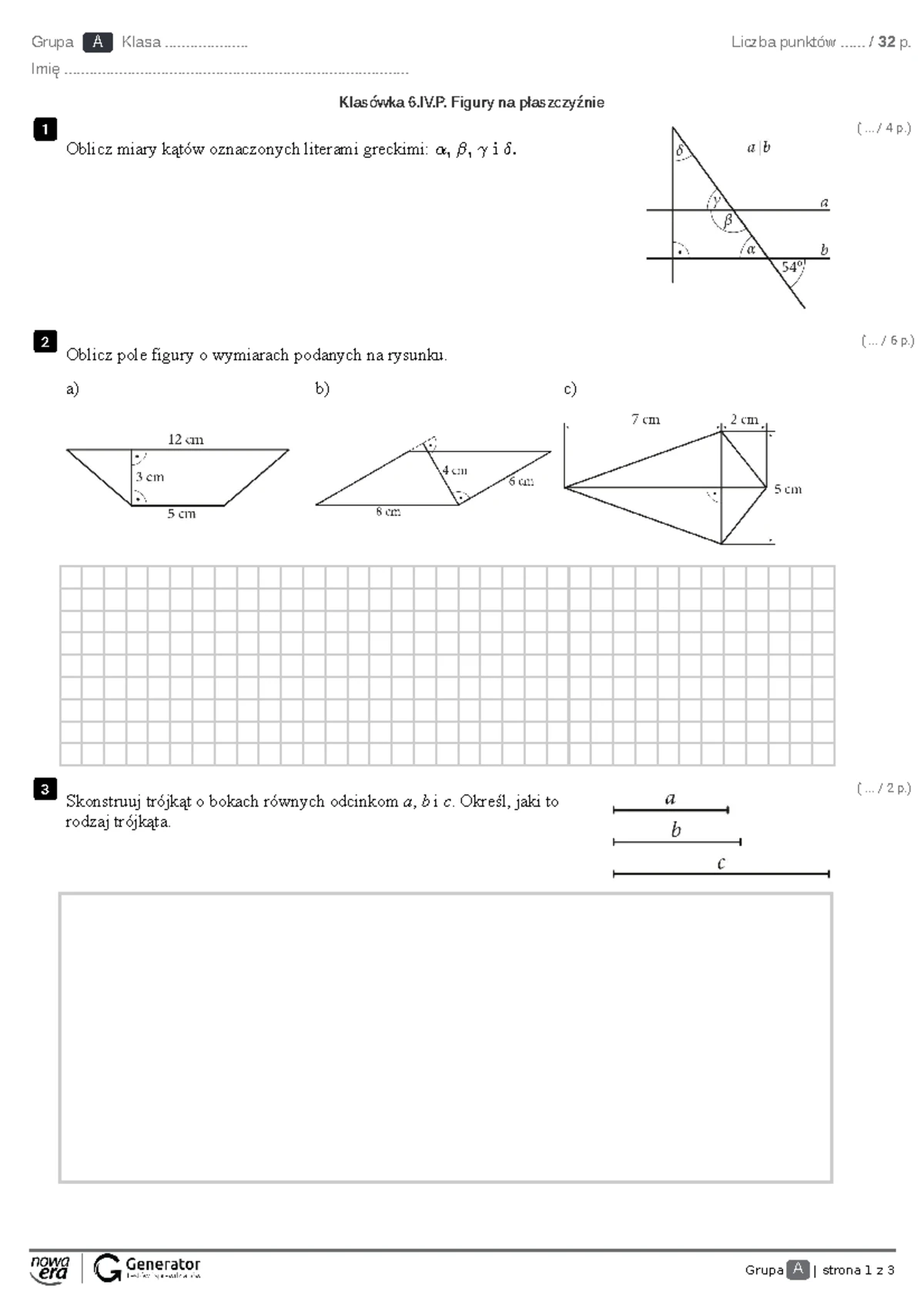
Sprawdzian Z Figur Na Płaszczyźnie 1 Gumnazjum

Nauka geometrii na poziomie pierwszego gimnazjum stanowi fundament dla dalszego rozwoju w obszarze matematyki i nauk ścisłych. Kluczowym elementem tego etapu jest opanowanie zagadnień związanych z figurami na płaszczyźnie. Sprawdzian z tego zakresu ma na celu weryfikację wiedzy i umiejętności uczniów w zakresie rozpoznawania, opisywania i podstawowych operacji na tych podstawowych obiektach geometrycznych. Zrozumienie tych pojęć jest niezbędne do dalszej nauki, gdzie pojawią się bardziej złożone bryły, przekształcenia geometryczne i zastosowania w fizyce czy inżynierii.

Czym są figury na płaszczyźnie i dlaczego są ważne?

Figury na płaszczyźnie to zbiory punktów leżących na tej samej prostej, czyli w dwuwymiarowej przestrzeni. Do najczęściej omawianych na tym poziomie należą między innymi: kwadrat, prostokąt, trójkąt (różnoboczny, równoboczny, równoramienny, prostokątny), koło, okrąg, romb, równoległobok i trapez. Każda z tych figur charakteryzuje się określonymi własnościami, takimi jak liczba boków, kątów, symetria, czy relacje między bokami i przekątnymi.

Znaczenie figur na płaszczyźnie wykracza poza sam program nauczania. Jak podkreśla wielu edukatorów, geometria płaska rozwija myślenie przestrzenne i logiczne rozumowanie.

"Zrozumienie podstawowych figur geometrycznych na płaszczyźnie jest jak nauka alfabetu dla języka geometrii. Bez tego, dalsze budowanie wiedzy staje się trudne, a nawet niemożliwe"

Wpływ sprawdzianu na rozwój ucznia

Sprawdzian z figur na płaszczyźnie jest dla ucznia pierwszego gimnazjum nie tylko testem wiedzy, ale także ważnym etapem rozwoju kompetencji matematycznych. Określa on, czy uczeń poprawnie przyswoił kluczowe definicje, wzory i potrafi je zastosować w praktyce. Problemy z tym sprawdzianem mogą sygnalizować trudności w pojmowaniu bardziej abstrakcyjnych pojęć geometrycznych, co wymaga natychmiastowej interwencji ze strony nauczyciela lub rodzica.

Kluczowe aspekty sprawdzianu obejmują:

• Rozpoznawanie figur: Czy uczeń potrafi odróżnić kwadrat od prostokąta, czy wie, czym różni się okrąg od koła?
• Znajomość definicji i własności: Czy uczeń zna pojęcia takie jak bok, wierzchołek, kąt, przekątna, promień? Czy potrafi wymienić kluczowe własności poszczególnych figur (np. kwadrat ma wszystkie boki równe i wszystkie kąty proste)?
• Obliczanie obwodu i pola: Czy uczeń potrafi zastosować odpowiednie wzory do obliczenia obwodu i pola prostokąta, kwadratu, trójkąta czy koła?
• Podstawowe konstrukcje i przekształcenia: W zależności od programu nauczania, sprawdzian może zawierać zadania dotyczące rysowania figur, podziału figur czy prostych przekształceń.

Niski wynik na sprawdzianie nie powinien być powodem do zniechęcenia, lecz impulsem do pracy nad własnymi słabościami. Regularne powtórki, rozwiązywanie dodatkowych zadań i korzystanie z pomocy dydaktycznych mogą znacząco poprawić zrozumienie materiału.

Zastosowania praktyczne figur na płaszczyźnie

Choć na pozór matematyka szkolna wydaje się abstrakcyjna, pojęcia związane z figurami na płaszczyźnie mają liczne zastosowania w życiu codziennym i w różnych zawodach. Przykłady obejmują:

• Architektura i budownictwo: Planowanie przestrzeni, projektowanie budynków, układanie płytek – wszystko to opiera się na geometrii płaskiej. Proste figury, jak prostokąty i kwadraty, tworzą podstawę większości konstrukcji.
• Projektowanie graficzne i sztuka: Tworzenie logo, stron internetowych, plakatów, a także malowanie czy rzeźbienie – wszędzie tam kluczowe są proporcje, kształty i kompozycje geometryczne.
• Codzienne czynności: Krojenie warzyw na równe plastry (prostokąty, koła), układanie mebli w pokoju, nawet krojenie tortu na równe kawałki – to wszystko przykłady wykorzystania podstawowej geometrii.
• Nawigacja: Mapy i plany miast opierają się na zasadach geometrii płaskiej, pozwalając na określenie odległości i kierunków.
• Inżynieria i produkcja: Projektowanie części maszyn, narzędzi, odzieży – precyzyjne wymiary i kształty są kluczowe dla funkcjonalności.

Nauczyciele często starają się pokazać uczniom te praktyczne powiązania, organizując lekcje w terenie, wykorzystując materiały plastyczne czy aplikacje komputerowe. Uczenie się o figurach na płaszczyźnie to nie tylko zdobywanie wiedzy teoretycznej, ale także rozwijanie umiejętności, które przydadzą się w wielu aspektach życia. Sprawdzian z tego zakresu stanowi ważny krok w tym procesie, motywując uczniów do głębszego zrozumienia i praktycznego zastosowania zdobytej wiedzy.