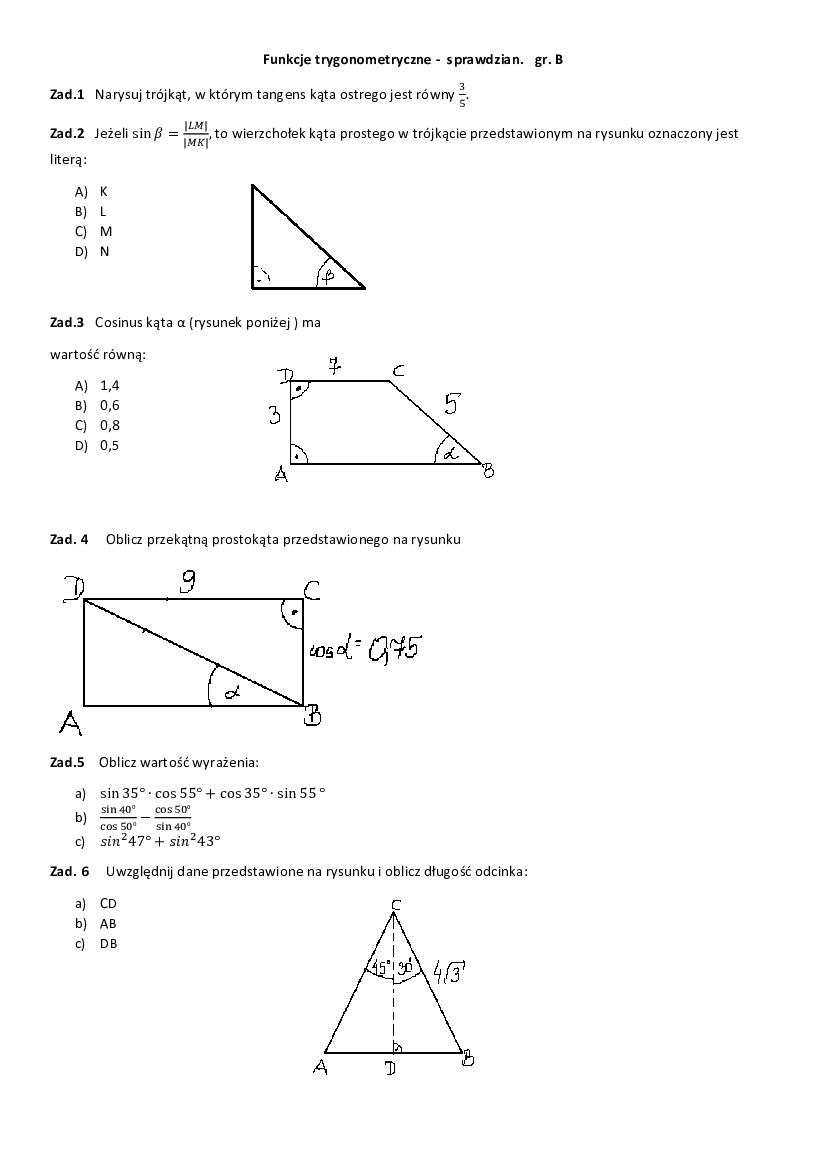
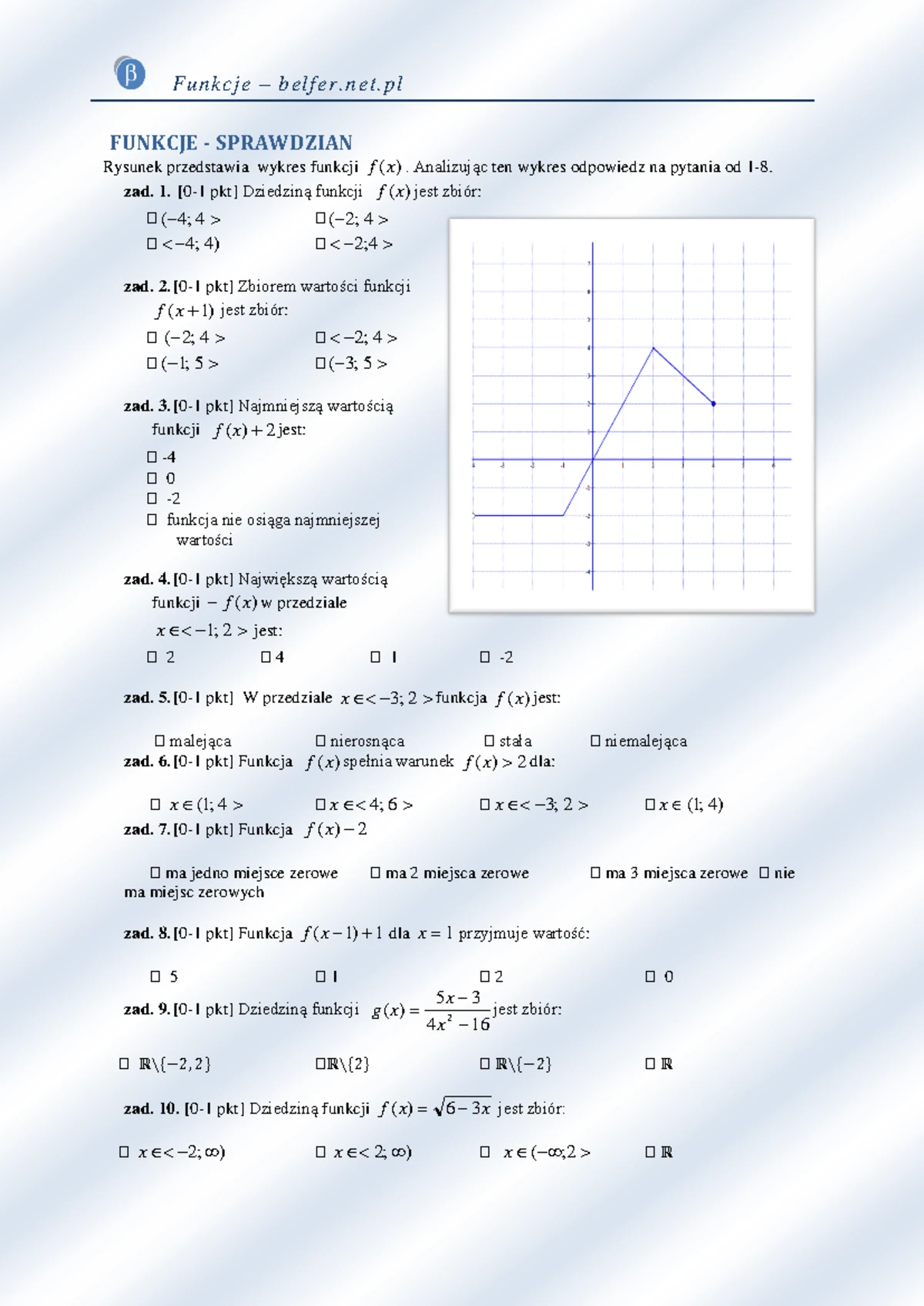
Sprawdzian Z Działu Trygonometria Liceum

Drogi Uczniu, doskonale wiemy, że dział trygonometrii w liceum potrafi być sporym wyzwaniem. Te wszystkie sinusy, cosinusy, tangensy, jednostka miary kąta w radianach… Brzmi znajomo? Nie martw się, nie jesteś sam. Wielu uczniów na początku czuje się zagubionych w świecie funkcji trygonometrycznych, a perspektywa sprawdzianu może budzić pewien niepokój. Ale mamy dla Ciebie dobrą wiadomość: trygonometria, choć może wydawać się skomplikowana, jest logiczna i, co najważniejsze, można ją opanować! Ten artykuł powstał po to, by Ci w tym pomóc. Skupimy się na kluczowych aspektach, które pojawią się na sprawdzianie, podamy proste wyjaśnienia i praktyczne wskazówki, jak się do tego zabrać.

Zrozumieć Podstawy: Kąty i Trójkąty

Zanim zanurzymy się w bardziej zaawansowane zagadnienia, warto wrócić do samych fundamentów. Trygonometria w liceum często zaczyna się od trójkąta prostokątnego. Pamiętasz jego budowę? Mamy przeciwprostokątną (najdłuższy bok, leżący naprzeciwko kąta prostego) oraz dwa przyprostokątne: jedną przeciwległą do danego kąta ostrogo i jedną przyległą do niego. Te relacje są kluczowe!

Najważniejsze funkcje trygonometryczne, które musisz znać na pamięć, to:

Sinus (sin): stosunek długości przyprostokątnej przeciwległej do danego kąta do długości przeciwprostokątnej. sin(α) = przyprostokątna przeciwległa / przeciwprostokątna
Cosinus (cos): stosunek długości przyprostokątnej przyległej do danego kąta do długości przeciwprostokątnej. cos(α) = przyprostokątna przyległa / przeciwprostokątna
Tangens (tg): stosunek długości przyprostokątnej przeciwległej do danego kąta do długości przyprostokątnej przyległej. tg(α) = przyprostokątna przeciwległa / przyprostokątna przyległa
Cotangens (ctg): odwrotność tangensa, czyli stosunek przyprostokątnej przyległej do przeciwległej. ctg(α) = przyprostokątna przyległa / przyprostokątna przeciwległa

Co z tymi kątami? Stopnie i Radiany

Na sprawdzianie na pewno pojawią się kąty wyrażone w stopniach (°), ale często też w radianach. To dwie różne miary tego samego – kąta. Pamiętaj o podstawowych relacjach:

180° = π radianów

Oznacza to, że:

90° to π/2 radianów
60° to π/3 radianów
45° to π/4 radianów
30° to π/6 radianów

Umiejętność zamiany stopni na radiany i odwrotnie jest niezwykle ważna. Zazwyczaj wystarczy zapamiętać te podstawowe wartości. Możesz też stosować prostą proporcję, jeśli masz wątpliwości.

Wartości Funkcji Trygonometrycznych dla Kątów Charakterystycznych

Kolejny kluczowy element sprawdzianu to znajomość wartości funkcji trygonometrycznych dla tzw. kątów charakterystycznych. Są to przede wszystkim kąty 30°, 45°, 60° (oraz ich odpowiedniki w radianach) oraz 0°, 90°, 180°, 270°, 360° (i ich odpowiedniki w radianach). Na pewno przyda Ci się tutaj tabelka wartości. Możesz ją narysować sama/sam lub wydrukować i mieć ją pod ręką podczas nauki.

Praktyczna wskazówka: Zamiast uczyć się na pamięć całej tabelki, spróbuj zrozumieć jej budowę. Na przykład, wartości sinusa dla 30°, 45°, 60° to pierwiastki z 1, 2, 3 podzielone przez 2. Wartości cosinusa to odwrotność tego, co dla sinusa (od większych do mniejszych). Tangens to sinus podzielony przez cosinus. Gdy zrozumiesz logikę, zapamiętanie będzie łatwiejsze!

Nie zapomnij też o wartościach dla kątów 0° i 90° (oraz ich odpowiednikach w radianach). Wartości sin(0°) = 0, cos(0°) = 1, tg(0°) = 0, sin(90°) = 1, cos(90°) = 0, a tg(90°) jest nieokreślony. To są proste zależności, które warto mieć w głowie.

Tożsamości Trygonometryczne – Niezbędne Narzędzia

Tożsamości trygonometryczne to takie "równania", które są prawdziwe dla każdego dopuszczalnego kąta. Są one jak narzędzia, które pozwalają nam przekształcać wyrażenia trygonometryczne, upraszczać je, a czasem dowodzić bardziej skomplikowanych twierdzeń. Na sprawdzianie na pewno pojawią się zadania wymagające ich zastosowania.

Najważniejsze, które musisz znać, to:

Podstawowa tożsamość trygonometryczna:

sin²(α) + cos²(α) = 1

To jest absolutny fundament! Dzięki niej możesz obliczyć wartość sinusa, jeśli znasz cosinus (lub odwrotnie), pamiętając tylko o znaku funkcji w odpowiedniej ćwiartce układu współrzędnych.
Tożsamości definiujące tangens i cotangens:

tg(α) = sin(α) / cos(α)

ctg(α) = cos(α) / sin(α)

Te również są bardzo praktyczne.

Mogą pojawić się też inne tożsamości, np. dotyczące sum i różnic kątów, czy kątów podwojonych, ale jeśli opanujesz te podstawowe, będziesz już o krok dalej.

Układ Współrzędnych i Ćwiartki

Gdy mówimy o kątach większych niż 90°, musimy sięgnąć do układu współrzędnych. Cały okrąg jednostkowy (o promieniu 1) dzielimy na cztery ćwiartki. Ważne jest, aby wiedzieć, w której ćwiartce leży dany kąt, ponieważ od tego zależy znak funkcji trygonometrycznych (czy są dodatnie, czy ujemne).

I ćwiartka (0° do 90°): Wszystkie funkcje (sin, cos, tg, ctg) są dodatnie.
II ćwiartka (90° do 180°): Tylko sinus jest dodatni. Cosinus, tangens i cotangens są ujemne.
III ćwiartka (180° do 270°): Tylko tangens i cotangens są dodatnie. Sinus i cosinus są ujemne.
IV ćwiartka (270° do 360°): Tylko cosinus jest dodatni. Sinus, tangens i cotangens są ujemne.

Sztuczka na zapamiętanie znaków: W klasie I często uczymy się rymowanki:

W pierwszej Wszystkie są dodatnie,
W drugiej Sinus tak samo.
W trzeciej Tangens nam dopomoże,
W czwartej Cosinus nasz kochany.

Znajomość znaków funkcji w poszczególnych ćwiartkach jest kluczowa, gdy obliczasz wartości dla kątów większych niż 90° czy korzystasz z tożsamości trygonometrycznych.

Rozwiązywanie Równań i Nierówności Trygonometrycznych

To może być najtrudniejsza część sprawdzianu, ale poćwiczysz ją na lekcjach. Rozwiązywanie równań typu sin(x) = 1/2 czy cos(x) = -1 wymaga znajomości funkcji trygonometrycznych dla kątów charakterystycznych i umiejętności rozszerzenia rozwiązania na cały zbiór liczb rzeczywistych. Pamiętaj o okresowości funkcji trygonometrycznych!

Okresowość oznacza, że funkcje trygonometryczne powtarzają swoje wartości co pewien interwał. Dla sinusa i cosinusa jest to 2π (lub 360°), a dla tangensa i cotangensa jest to π (lub 180°). Dlatego po znalezieniu jednego rozwiązania, dodajemy wielokrotność okresu, np. x = π/6 + 2kπ, gdzie k jest dowolną liczbą całkowitą.

Praktyczne Rady na Dzień Sprawdzianu

Zbliża się sprawdzian, co robić? Oto kilka sprawdzonych rad:

Powtórz podstawy: Upewnij się, że doskonale rozumiesz definicje sinusa, cosinusa, tangensa i cotangensa w trójkącie prostokątnym.
Tabelka wartości: Zrób sobie swoją tabelkę wartości dla kątów charakterystycznych i przećwicz ją.
Tożsamości to podstawa: Przypomnij sobie kluczowe tożsamości i spróbuj je zastosować w prostych przykładach.
Układ współrzędnych: Zrozum, jak kąty wpływają na znaki funkcji w poszczególnych ćwiartkach.
Ćwicz, ćwicz, ćwicz! Rozwiązuj zadania z podręcznika, zeszytu ćwiczeń, arkuszy z poprzednich lat. Im więcej przykładów przerobisz, tym pewniej poczujesz się na sprawdzianie.
Nie panikuj: Jeśli natkniesz się na trudne zadanie, zrób krok w tył, spróbuj zidentyfikować, jakie narzędzia (tożsamości, definicje) możesz zastosować.
Zadbaj o siebie: W przeddzień sprawdzianu dobrze się wyśpij i zjedz śniadanie.

Trygonometria to piękny dział matematyki, który znajduje zastosowanie w wielu dziedzinach życia, od fizyki i inżynierii po grafikę komputerową. Pamiętaj, że każdy ma prawo do momentów zwątpienia, ale determinacja i systematyczna praca przyniosą efekty. Wierzymy w Ciebie! Powodzenia na sprawdzianie!