Sprawdzian Z Dzialu Trojkaty Prostokatne

Sprawdzian z działu trójkąty prostokątne to kluczowe narzędzie oceny zrozumienia przez uczniów fundamentalnych pojęć związanych z tym specyficznym typem trójkąta. Trójkąt prostokątny, charakteryzujący się jednym kątem o mierze 90 stopni, stanowi bazę dla wielu zagadnień matematycznych, a jego właściwości odgrywają niebagatelną rolę w dalszej edukacji, sięgając od geometrii przestrzennej po analizę matematyczną. Zrozumienie jego cech, takich jak przyprostokątne, przeciwprostokątna oraz twierdzenie Pitagorasa, jest niezbędne do efektywnego rozwiązywania problemów i budowania dalszej wiedzy matematycznej.

Kluczowe Elementy Sprawdzianu z Trójkątów Prostokątnych

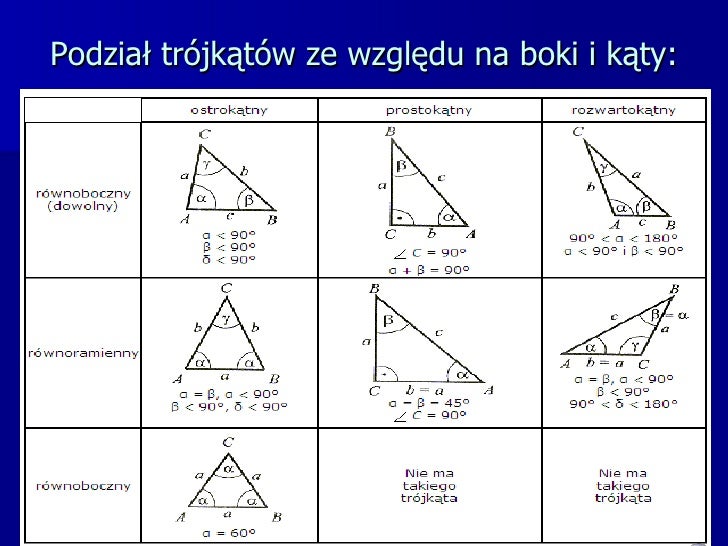
Definicja i Podstawowe Właściwości

Sednem każdego sprawdzianu z trójkątów prostokątnych jest weryfikacja, czy uczeń potrafi poprawnie zdefiniować ten obiekt. Podstawowa definicja mówi, że jest to trójkąt posiadający jeden kąt wewnętrzny o mierze 90 stopni. Kolejnym nieodzownym elementem jest identyfikacja i nazewnictwo jego boków. Boki tworzące kąt prosty nazywane są przyprostokątnymi, natomiast bok leżący naprzeciwko kąta prostego to przeciwprostokątna. Ta precyzja terminologiczna jest fundamentem, na którym buduje się dalsze, bardziej złożone rozumienie. Sprawdzian będzie zatem zawierał zadania polegające na rozpoznawaniu tych elementów na rysunkach, opisywaniu ich relacji oraz stosowaniu odpowiedniego słownictwa.

Twierdzenie Pitagorasa – Serce Zagadnienia

Bez wątpienia najważniejszym zagadnieniem w kontekście trójkątów prostokątnych jest twierdzenie Pitagorasa. Sprawdzian poświęcony temu działowi nie może obejść się bez zadań weryfikujących znajomość i umiejętność stosowania tego twierdzenia. Twierdzenie to stanowi fundamentalny związek między długościami boków trójkąta prostokątnego, wyrażony równaniem: $a^2 + b^2 = c^2$, gdzie 'a' i 'b' to długości przyprostokątnych, a 'c' to długość przeciwprostokątnej. Umiejętność jego zastosowania do obliczania brakującej długości boku, gdy znane są dwie pozostałe, jest absolutnym priorytetem. Sprawdziany często zawierają zadania otwarte, wymagające przeprowadzenia obliczeń, jak i zadania zamknięte, sprawdzające rozumienie samego twierdzenia i jego konsekwencji.

Pole i Obwód Trójkąta Prostokątnego

Oprócz twierdzenia Pitagorasa, sprawdziany weryfikują także znajomość wzorów na pole i obwód trójkąta prostokątnego. Pole trójkąta prostokątnego jest szczególnie proste do obliczenia – wynosi połowę iloczynu długości jego przyprostokątnych: $P = \frac{1}{2}ab$. Obwód to suma długości wszystkich boków: $O = a + b + c$. Zrozumienie tych prostych wzorów, w połączeniu z umiejętnością obliczania boków za pomocą twierdzenia Pitagorasa, pozwala na rozwiązanie szerokiej gamy zadań geometrycznych. Sprawdziany mogą zawierać zadania wymagające obliczenia pola lub obwodu na podstawie podanych długości boków, lub odwrotnie – obliczenia długości boków na podstawie pola i jednej z przyprostokątnych, czy obwodu i jednej z przyprostokątnych.

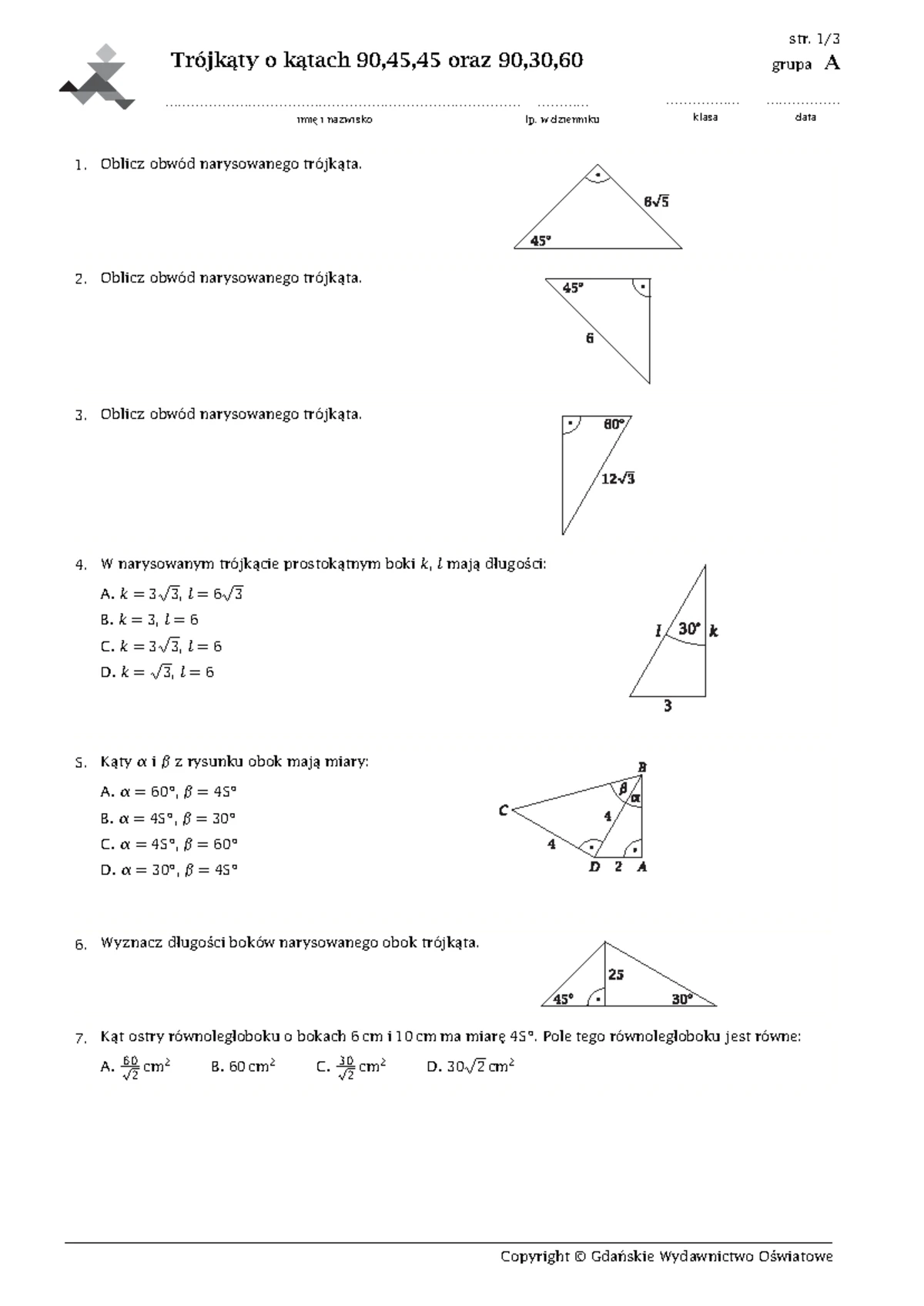
Trójkąty Prostokątne Specjalne

W programie nauczania często pojawiają się również trójkąty prostokątne specjalne, takie jak trójkąt prostokątny równoramienny (o kątach 45, 45, 90 stopni) oraz trójkąty prostokątne o kątach 30, 60, 90 stopni. Znajomość ich proporcji boków, które wynikają z twierdzenia Pitagorasa, znacząco ułatwia rozwiązywanie zadań. Na przykład, w trójkącie o kątach 45, 45, 90 stopni przyprostokątne są sobie równe, a przeciwprostokątna jest $\sqrt{2}$ razy dłuższa od przyprostokątnej. W trójkącie o kątach 30, 60, 90 stopni przeciwprostokątna jest dwukrotnie dłuższa od krótszej przyprostokątnej, a dłuższa przyprostokątna jest $\sqrt{3}$ razy dłuższa od krótszej. Sprawdziany mogą zawierać zadania wymagające rozpoznania tych typów trójkątów i zastosowania ich specyficznych właściwości.

Dlaczego Sprawdzian z Trójkątów Prostokątnych Ma Znaczenie?

Fundament Dalszej Nauki Matematyki

Trójkąty prostokątne i związane z nimi twierdzenie Pitagorasa stanowią kamień węgielny dla wielu bardziej zaawansowanych koncepcji matematycznych. Bez solidnego zrozumienia tych podstaw, uczniowie mogą napotkać poważne trudności w dalszej nauce trygonometrii, geometrii analitycznej, a nawet w działach fizyki, które opierają się na analizie wektorowej i analizie ruchu. Jak podkreśla wielu pedagogów, "solidne podstawy matematyczne są kluczem do sukcesu w naukach ścisłych". Sprawdzian z tego działu pozwala na wczesne zidentyfikowanie ewentualnych luk w wiedzy, umożliwiając podjęcie działań naprawczych zanim problemy staną się zbyt trudne do rozwiązania.

Rozwój Umiejętności Analitycznego Myślenia

Rozwiązywanie zadań z trójkątów prostokątnych wymaga nie tylko znajomości wzorów, ale także umiejętności logicznego myślenia, analizy problemu i wyciągania wniosków. Uczniowie muszą nauczyć się identyfikować dane, szukać zależności między nimi, wybierać odpowiednie narzędzia matematyczne (jak twierdzenie Pitagorasa) i interpretować otrzymane wyniki. Ten proces jest nieoceniony dla rozwoju umiejętności analitycznego myślenia, które są przydatne nie tylko w matematyce, ale także w każdej dziedzinie życia wymagającej rozwiązywania problemów.

Praktyczne Zastosowania w Codziennym Życiu i Poza Szkołą

Choć może się to wydawać zaskakujące, pojęcia związane z trójkątami prostokątnymi mają zaskakująco wiele praktycznych zastosowań. Architekci i budowlańcy wykorzystują twierdzenie Pitagorasa do obliczania długości przekątnych, wysokości i innych elementów konstrukcyjnych, zapewniając stabilność i bezpieczeństwo budynków. Projektanci mebli używają tych zasad do tworzenia proporcjonalnych i funkcjonalnych projektów. Nawet w codziennych czynnościach, takich jak ustawianie drabiny pod odpowiednim kątem, czy sprawdzanie, czy prostokątny mebel zmieści się w rogu pokoju, nieświadomie stosujemy wiedzę o trójkątach prostokątnych. W szkołach, nauczanie o trójkątach prostokątnych często wiąże się z zadaniami praktycznymi, np. obliczaniem odległości między punktami na mapie, czy wyznaczaniem wysokości drzewa za pomocą cienia i podobieństwa trójkątów, co utrwala praktyczne znaczenie tych zagadnień.

Jak Sprawdzian Wpływa na Uczniów?

Sprawdzian z trójkątów prostokątnych może być źródłem zarówno stresu, jak i satysfakcji dla ucznia. Dla tych, którzy systematycznie pracowali i dobrze opanowali materiał, jest to okazja do potwierdzenia swoich umiejętności i zdobycia pozytywnej oceny. Dla innych, może stanowić sygnał, że potrzebują dodatkowego wsparcia i czasu na zrozumienie zagadnienia. Kluczowe jest, aby sprawdzian był traktowany nie tylko jako forma oceny, ale także jako narzędzie diagnostyczne. Informacje zwrotne uzyskane po sprawdzianie, zarówno przez ucznia, jak i nauczyciela, pozwalają na dalsze ukierunkowanie procesu nauczania i uczenia się. Ważne jest, aby uczniowie rozumieli cel sprawdzianu – nie tylko ocenę, ale przede wszystkim możliwość sprawdzenia swojej wiedzy i umiejętności, co jest nieodłącznym elementem procesu edukacyjnego.