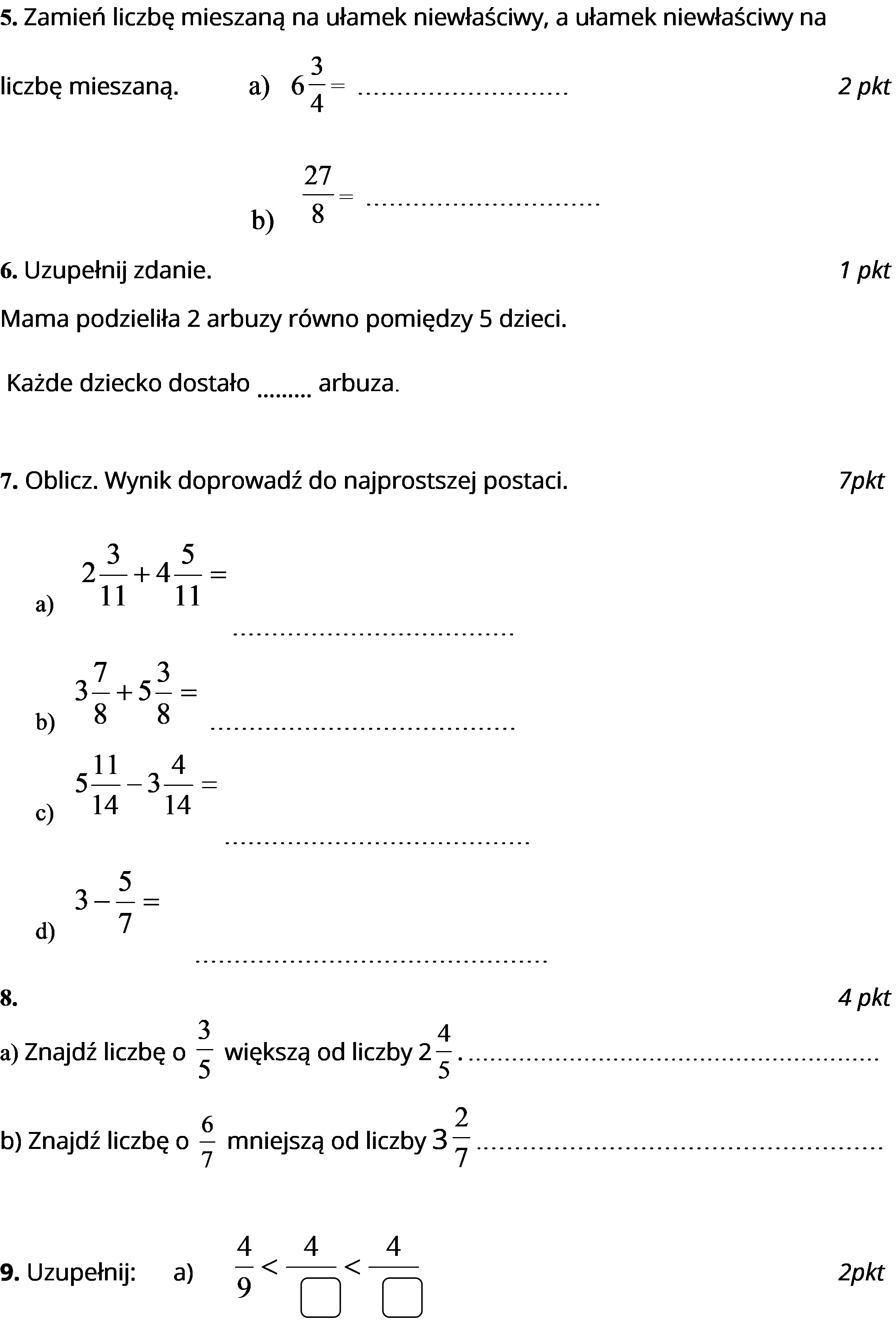Sprawdzian Wiadomości Z Ułamków Zwykłych

Rozumiemy, że perspektywa kolejnego sprawdzianu może budzić pewien niepokój, a temat ułamków zwykłych bywa postrzegany jako jeden z tych obszarów matematyki, który sprawia najwięcej kłopotów. Wielu uczniów zastanawia się, po co właściwie są nam potrzebne te wszystkie kreski, liczniki i mianowniki. Czy naprawdę mamy je stosować w codziennym życiu? Odpowiedź brzmi: tak! Ułamki to nie tylko szkolne zadania, to uniwersalny język opisujący części całości, który otacza nas na każdym kroku.

Ułamki w Codziennym Życiu: Więcej Niż Myślimy

Pomyślmy o sytuacji, gdy dzielimy pizzę między przyjaciół. Każdy dostaje część tej całości. Jeśli dzielimy pizzę na 8 równych kawałków i każdy zjada po 2, to zjada 2/8 pizzy. Jeśli przepis na ciasto wymaga 1 i 1/2 szklanki mąki, to właśnie mamy do czynienia z liczbami mieszanymi, które są ściśle powiązane z ułamkami. Planując zakupy, często widzimy promocje typu "kup 2, zapłać za 1 i 1/2" – to kolejny przykład ułamków w akcji.

Nawet takie proste czynności jak odmierzanie czasu mogą być związane z ułamkami. Pół godziny to 1/2 godziny, a kwadrans to 1/4 godziny. W świecie majsterkowania czy gotowania, precyzyjne odmierzanie składników czy materiałów niemal zawsze opiera się na ułamkach. Czy kiedykolwiek zastanawialiście się nad tym, jak architekci obliczają proporcje czy jak kucharze odmierzają potrzebne ilości przypraw? Wszędzie tam pojawiają się ułamki.

Dlaczego Zrozumienie Ułamków Jest Kluczowe?

Niektórzy mogą argumentować, że w dzisiejszych czasach wszystko można łatwo przeliczyć za pomocą kalkulatora, więc dogłębne rozumienie ułamków nie jest już tak istotne. Oczywiście, technologia jest potężnym narzędziem, ale bez podstawowego zrozumienia tego, co się za tymi liczbami kryje, możemy popełniać błędy lub po prostu nie rozumieć kontekstu. Kalkulator powie nam, że 1/3 to w przybliżeniu 0.333, ale czy wiemy, dlaczego tak jest? Czy potrafimy ocenić, czy wynik jest sensowny w danym kontekście?

Zrozumienie ułamków to fundament dla wielu bardziej zaawansowanych koncepcji matematycznych, takich jak procenty, stosunki czy prawdopodobieństwo. Bez tej podstawy, kolejne etapy nauki mogą stać się trudniejsze i bardziej frustrujące. Ułamki uczą nas również logicznego myślenia i umiejętności rozkładania problemów na mniejsze, łatwiejsze do rozwiązania części.

Przygotowanie do Sprawdzianu: Klucz do Sukcesu

Wiemy, że zbliża się sprawdzian z ułamków zwykłych. To naturalne, że chcecie się do niego dobrze przygotować. Kluczem do sukcesu jest nie tylko zapamiętywanie wzorów, ale przede wszystkim zrozumienie koncepcji stojących za działaniami na ułamkach.

Przyjrzyjmy się kilku kluczowym zagadnieniom, które zazwyczaj pojawiają się na sprawdzianach:

Rozumienie pojęcia ułamka: Co to jest licznik, co to jest mianownik i co one reprezentują. Pamiętajmy, że mianownik mówi nam, na ile równych części została podzielona całość, a licznik mówi, ile z tych części bierzemy pod uwagę.
Zamiana ułamków: Umiejętność zamiany ułamków niewłaściwych na liczby mieszane i odwrotnie. To jak przekładanie pomiędzy dwoma językami – potrzebne, by móc swobodnie wyrażać te same myśli w różny sposób.
Rozszerzanie i skracanie ułamków: Znajdowanie ułamków równoważnych. To klucz do porównywania i dodawania ułamków o różnych mianownikach. Wyobraźmy sobie, że chcemy porównać 1/2 i 2/4 pizzy – to te same ilości, mimo że liczby wyglądają inaczej.
Porównywanie ułamków: Umiejętność określenia, który ułamek jest większy, a który mniejszy. Często wymaga to sprowadzenia ułamków do wspólnego mianownika, co jest bezpośrednio związane z rozszerzaniem.
Dodawanie i odejmowanie ułamków: Tutaj kluczowe jest znalezienie wspólnego mianownika, co pozwala nam na "wyrównanie" wielkości kawałków, zanim je dodamy lub odejmiemy.
Mnożenie ułamków: Prostowanie, jak mnożymy liczniki i mianowniki. To operacja, która często wydaje się prostsza, bo nie wymaga wspólnego mianownika.
Dzielenie ułamków: Tutaj pojawia się zasada "zamień dzielenie na mnożenie przez odwrotność drugiego ułamka". To technika, która pozwala nam rozwiązać problem dzielenia części na jeszcze mniejsze części.

Rozwiązywanie Problemów: Przykładowe Zadania

Zastanówmy się nad typowym problemem: "Janek zjadł 1/4 tortu, a Kasia zjadła 1/3 tego samego tortu. Jaką część tortu zjedli razem?"

Aby rozwiązać to zadanie, musimy dodać ułamki 1/4 i 1/3. Najpierw znajdujemy wspólny mianownik dla 4 i 3, który wynosi 12. Następnie rozszerzamy ułamki:

1/4 = 3/12
1/3 = 4/12

Teraz możemy dodać: 3/12 + 4/12 = 7/12. Razem zjedli 7/12 tortu.

Inny przykład: "Mama kupiła 2 kg jabłek. Do szarlotki zużyła 2/3 tych jabłek. Ile kilogramów jabłek zostało?"

Tutaj musimy obliczyć, ile jabłek zużyła mama, a następnie odjąć tę ilość od początkowej. Najpierw obliczamy 2/3 z 2 kg. Mnożymy: 2 * (2/3) = 4/3 kg. Teraz odejmujemy tę ilość od 2 kg: 2 - 4/3. Aby to zrobić, zamieniamy 2 na ułamek z mianownikiem 3: 6/3. Odejmujemy: 6/3 - 4/3 = 2/3 kg. Zostało 2/3 kg jabłek.

Przeciwne Opinie i Jak Sobie z Nimi Radzić

Jak wspomnieliśmy wcześniej, niektórzy mogą twierdzić, że ułamki są przestarzałe lub niepotrzebne w erze cyfrowej. To prawda, że kalkulatory i komputery ułatwiają obliczenia, ale nie zastąpią one zrozumienia. Bez niego trudno jest interpretować wyniki, tworzyć nowe rozwiązania czy nawet prawidłowo formułować problemy. Wyobraźmy sobie mechanika samochodowego, który nie rozumie działania silnika, a jedynie zna przyciski na komputerze diagnostycznym – to byłaby ryzykowna sytuacja.

Innym argumentem może być to, że ułamki są po prostu trudne i frustrujące. To naturalne uczucie, gdy napotykamy coś nowego i skomplikowanego. Jednakże, z odpowiednim podejściem, cierpliwością i praktyką, nawet najtrudniejsze zagadnienia stają się bardziej przystępne. Kluczem jest znalezienie metody nauki, która najlepiej odpowiada naszym indywidualnym potrzebom.

Strategie Uczenia się i Przygotowania

Jak zatem podejść do nauki i przygotowania się do sprawdzianu w sposób efektywny?

Powtórz podstawy: Upewnij się, że rozumiesz definicje i znaczenie licznika i mianownika.
Wizualizuj: Używaj rysunków, diagramów, kostek do zabawy, pokrojonych owoców – wszystkiego, co pomoże Ci zobaczyć ułamki jako części całości. Na przykład, podziel prostokąt na 5 równych części i zaznacz 2, aby zobaczyć 2/5.
Ćwicz, ćwicz, ćwicz: Rozwiązywanie zadań jest najważniejsze. Zacznij od prostych przykładów i stopniowo przechodź do trudniejszych.
Korzystaj z różnych źródeł: Oprócz podręcznika, poszukaj materiałów online, filmów instruktażowych, gier edukacyjnych. Różnorodność może pomóc w lepszym zrozumieniu materiału.
Pracuj z innymi: Uczenie się w grupie może być bardzo pomocne. Możecie wyjaśniać sobie nawzajem wątpliwości i wspólnie rozwiązywać zadania.
Nie bój się pytać: Jeśli czegoś nie rozumiesz, zapytaj nauczyciela, kolegę lub poszukaj odpowiedzi.
Skup się na zrozumieniu, nie na zapamiętywaniu: Zamiast uczyć się na pamięć algorytmów, staraj się zrozumieć, dlaczego dany algorytm działa.

Podsumowanie i Kierunek na Przyszłość

Sprawdzian z ułamków zwykłych to ważny etap w nauce matematyki. Pokonanie tego wyzwania nie tylko przygotuje Was do kolejnych lekcji, ale także da Wam narzędzia do lepszego rozumienia świata wokół Was. Ułamki to język opisujący proporcje, podziały i relacje – a ten język jest niezbędny w tak wielu dziedzinach życia.

Pamiętajcie, że każdy napotyka trudności. Ważne jest, aby podejść do nauki z pozytywnym nastawieniem i determinacją. Każde rozwiązane zadanie, każde zrozumiane pojęcie to krok naprzód. Cieszcie się z małych sukcesów i nie zrażajcie się chwilowymi niepowodzeniami.

Czy czujecie się teraz lepiej przygotowani do zmierzenia się z ułamkami? Jakie metody nauki okazały się dla Was najskuteczniejsze?