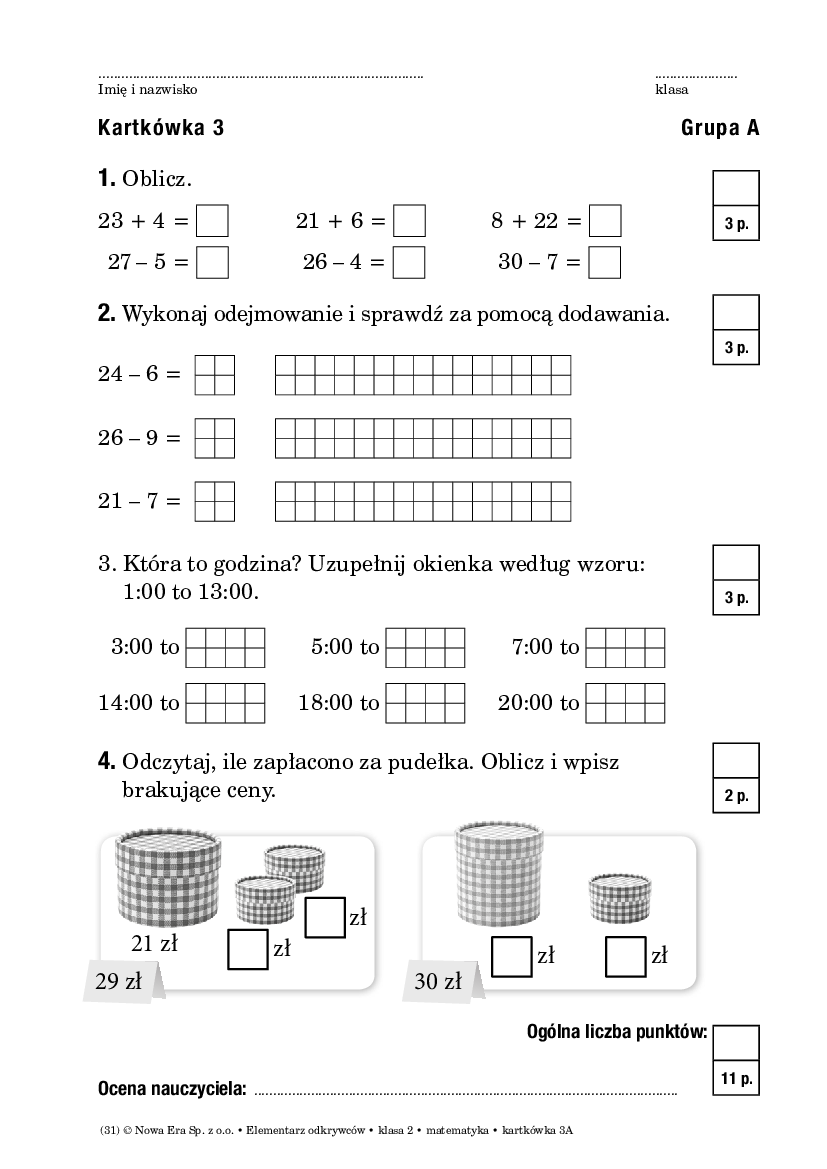
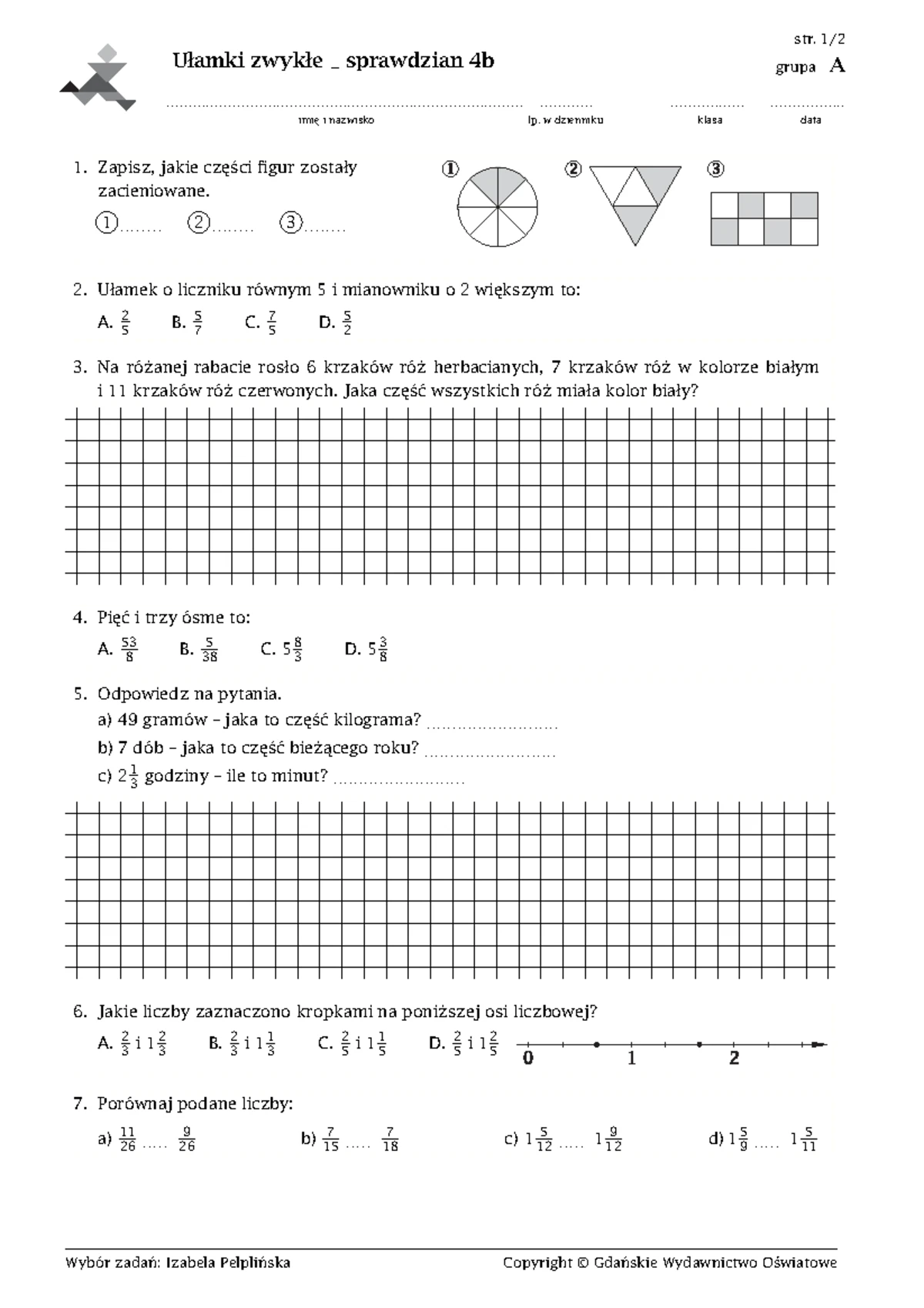
Sprawdzian Semestralny Z Matematyki Kl 3

Sprawdzian semestralny z matematyki dla klasy 3 to podsumowujące narzędzie oceny, które ma na celu sprawdzenie poziomu wiedzy i umiejętności ucznia zdobytych w ciągu pierwszego semestru nauki. Obejmuje on materiał przerobiony od początku roku szkolnego do momentu przeprowadzenia sprawdzianu, koncentrując się na kluczowych zagadnieniach danego programu nauczania.
Główne aspekty sprawdzianu semestralnego obejmują:
-
Zakres materiału: Sprawdzian obejmuje cały materiał teoretyczny i praktyczny zrealizowany w pierwszym semestrze. Nauczyciel zazwyczaj określa konkretne działy matematyki, które będą sprawdzane.
-
Rodzaje zadań: Zazwyczaj występują tu zadania o różnym stopniu trudności, od prostych zadań zamkniętych (np. jednokrotnego lub wielokrotnego wyboru) po zadania otwarte wymagające samodzielnego rozwiązania i przedstawienia toku rozumowania.
-
Umiejętności sprawdzane: Sprawdzian ocenia nie tylko znajomość wzorów i definicji, ale przede wszystkim umiejętność ich zastosowania w praktycznych zadaniach. Obejmuje to analizę problemu, wybór odpowiedniej metody rozwiązania, poprawne wykonanie obliczeń oraz interpretację wyników.
-
Forma oceny: Wynik sprawdzianu semestralnego stanowi ważny element oceny śródrocznej, wpływając na ogólną ocenę z matematyki na półrocze.
-
Cel diagnostyczny: Oprócz funkcji oceniającej, sprawdzian ma również cel diagnostyczny. Pozwala uczniowi zidentyfikować swoje mocne i słabe strony w opanowaniu materiału, a nauczycielowi dostosować metody pracy na kolejnym semestrze.
Przykłady prostych zadań:
-
Oblicz wartość wyrażenia: $5 \times (12 - 7) + 15$. Poprawna odpowiedź wymaga wykonania najpierw działania w nawiasie, następnie mnożenia, a na końcu dodawania.
-
Rozwiąż równanie: $2x + 8 = 20$. Tutaj należy zastosować odpowiednie operacje algebraiczne, aby wyznaczyć niewiadomą $x$.
Sprawdzian semestralny z matematyki ma kluczowe znaczenie dla utrwalenia i podsumowania wiedzy. Dobre przygotowanie do niego pomaga nie tylko w uzyskaniu pozytywnej oceny, ale także w pewniejszym przejściu do materiału kolejnego semestru. Ponadto, umiejętności matematyczne rozwijane na tym etapie mają swoje realne zastosowania w codziennym życiu, od prostych obliczeń finansowych po bardziej złożone analizy i rozwiązywanie problemów.