Sprawdzian Pola Figur Płaskich Gimnazjum

Sprawdziany z pola figur płaskich w gimnazjum to moment, który dla wielu uczniów wiąże się z pewnym stresem. Jednak właściwe przygotowanie i zrozumienie kluczowych zagadnień mogą zamienić ten sprawdzian w szansę na udowodnienie swojej wiedzy. W tym artykule przyjrzymy się, co zazwyczaj zawiera taki sprawdzian, jak się do niego efektywnie przygotować, a także dlaczego umiejętność obliczania pola figur jest ważna w życiu codziennym.

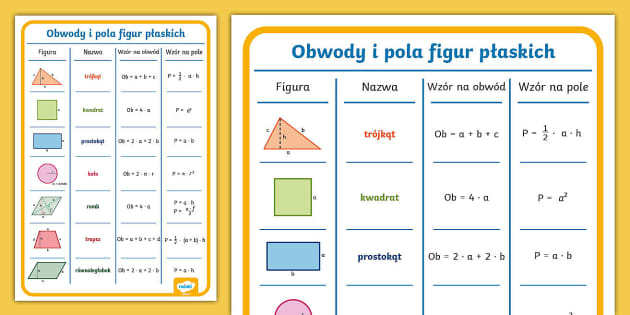
Kluczowe figury i wzory

Podstawą każdego sprawdzianu z pola figur płaskich są oczywiście znajomość podstawowych figur geometrycznych i ich charakterystycznych cech. W gimnazjum skupiamy się przede wszystkim na:

Kwadrat

Kwadrat to figura o czterech równych bokach i czterech kątach prostych. Jest to najbardziej podstawowa figura, a jej pole obliczamy za pomocą prostego wzoru: P = a², gdzie 'a' to długość boku kwadratu. Na sprawdzianie możemy spotkać zadania polegające na obliczeniu pola kwadratu o podanym boku, lub odwrotnie – obliczeniu długości boku, jeśli znamy pole. Warto pamiętać, że kwadrat jest również szczególnym przypadkiem prostokąta.

Prostokąt

Prostokąt charakteryzuje się dwoma parami równoległych boków o równej długości i czterema kątami prostymi. Wzór na pole prostokąta to: P = a * b, gdzie 'a' i 'b' to długości jego boków. Zadania mogą wymagać obliczenia pola prostokąta, albo, jeśli znamy pole i jeden bok, wyznaczenia długości drugiego boku.

Trójkąt

Trójkąt, figura o trzech bokach, to już nieco bardziej złożona kwestia. Istnieje wiele rodzajów trójkątów (równoboczne, równoramienne, prostokątne, różnoboczne), ale podstawowy wzór na pole trójkąta pozostaje ten sam: P = (a * h) / 2, gdzie 'a' to długość boku (podstawa), a 'h' to wysokość opuszczona na ten bok. Kluczowe jest tutaj umiejętne rozpoznanie podstawy i odpowiedniej wysokości. W przypadku trójkątów prostokątnych, przyprostokątne mogą pełnić rolę podstawy i wysokości, co znacznie upraszcza obliczenia. Sprawdziany często zawierają zadania, gdzie trzeba samodzielnie wyznaczyć wysokość na podstawie innych danych, np. długości boków w trójkącie równobocznym, gdzie stosuje się wzór h = (a√3)/2.

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Wzór na jego pole jest analogiczny do wzoru na pole trójkąta: P = a * h, gdzie 'a' to długość boku (podstawa), a 'h' to wysokość opuszczona na tę podstawę. Ważne jest, aby rozróżnić wysokość od długości boku nachylonego. Zrozumienie, że równoległobok można "przekształcić" w prostokąt o tym samym polu, często pomaga w wizualizacji wzoru.

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Wzór na jego pole to: P = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw (równoległych boków), a 'h' to wysokość (odległość między podstawami). Rozpoznanie, które boki są podstawami, a która jest wysokością, jest kluczowe. Warto pamiętać o różnych rodzajach trapezów – równoramiennych, prostokątnych – ale wzór na pole pozostaje uniwersalny.

Koło

Koło to figura definiowana przez wszystkie punkty jednakowo oddalone od środka. Wzór na pole koła to: P = πr², gdzie 'r' to promień koła, a 'π' (pi) to stała matematyczna (w przybliżeniu 3.14). Często na sprawdzianach podaje się promień, ale czasem może być potrzebne obliczenie go na podstawie średnicy (d = 2r) lub obwodu (Obw = 2πr).

Zadania złożone i kombinowane

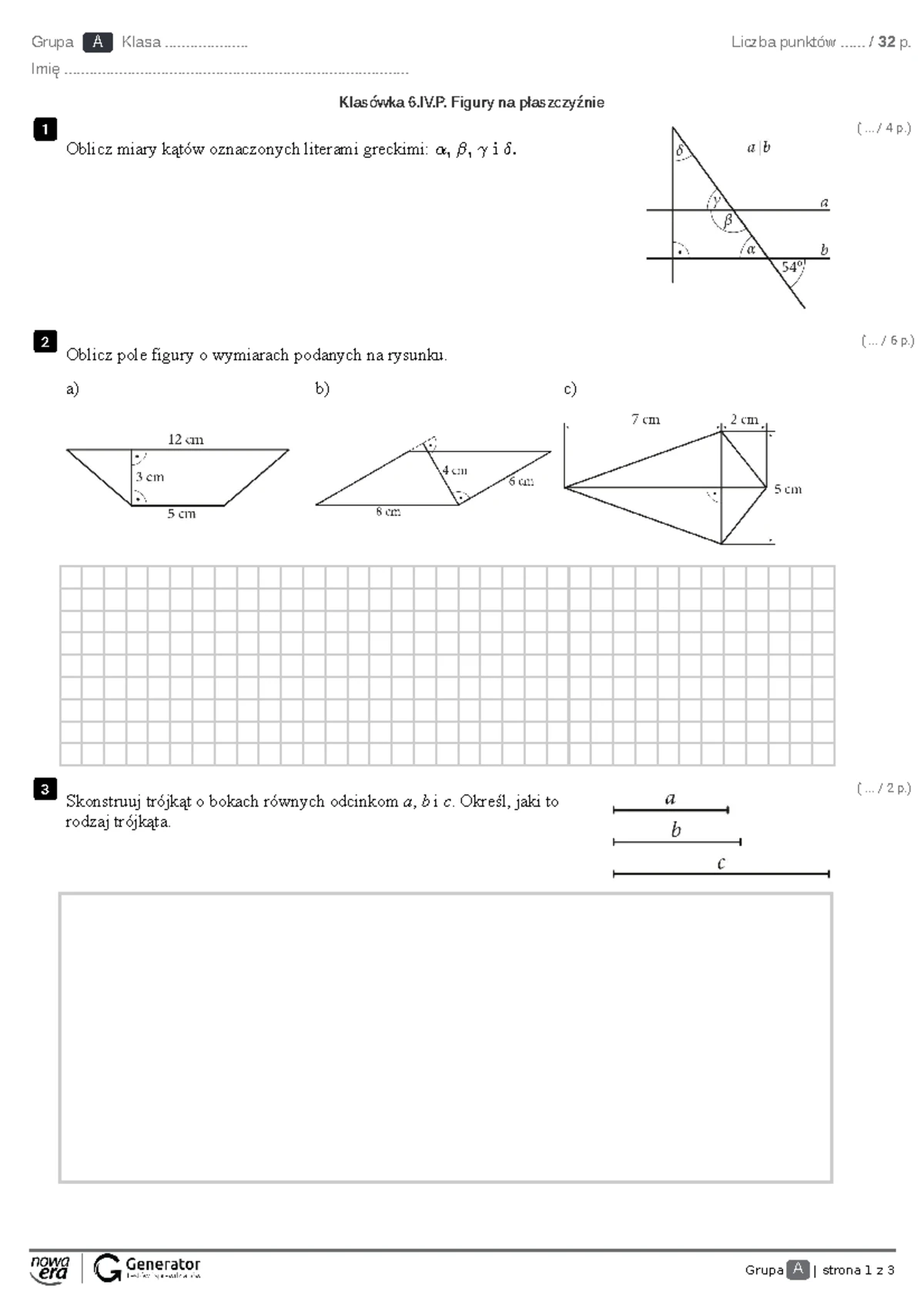
Sprawdziany często nie ograniczają się do prostego zastosowania jednego wzoru. Mogą pojawić się zadania wymagające połączenia kilku figur. Na przykład, pole skomplikowanego kształtu może być sumą pól prostokąta i trójkąta, lub różnicą między polem większej figury a polem mniejszej. Wymaga to dokładnej analizy rysunku i rozłożenia go na prostsze elementy.

Często spotykane są również zadania z nieznanymi wymiarami, gdzie należy je najpierw obliczyć, korzystając z innych danych geometrycznych lub algebraicznych. Przykładem może być sytuacja, gdzie znamy pole prostokąta i stosunek długości jego boków, a musimy wyznaczyć konkretne wymiary.

Jednostki miary odgrywają również kluczową rolę. Należy zwracać uwagę na to, czy wszystkie wymiary podane są w tych samych jednostkach (np. centymetrach, metrach). Jeśli nie, konieczne jest dokonanie konwersji przed przystąpieniem do obliczeń. Wynik pola powinien być wyrażony w jednostkach kwadratowych (np. cm², m²).

Strategie efektywnego przygotowania

Aby dobrze przygotować się do sprawdzianu z pola figur płaskich, warto zastosować kilka sprawdzonych metod:

Systematyczne powtarzanie wzorów

Najważniejsze jest opanowanie wszystkich podstawowych wzorów. Nie wystarczy je znać – trzeba je rozumieć. Warto wypisać je wszystkie na kartce, często je przeglądać, a nawet próbować odtwarzać z pamięci. Tworzenie fiszek może być bardzo pomocne.

Rozwiązywanie zadań

Teoria bez praktyki jest mało wartościowa. Rozwiązywanie dużej liczby zadań jest kluczowe. Zacznij od tych najprostszych, bazujących na jednym wzorze, a następnie przechodź do zadań bardziej złożonych, wymagających kombinacji, wyznaczania nieznanych danych czy pracy z jednostkami. Korzystaj z podręcznika, zbiorów zadań, a także materiałów dostępnych online.

Zrozumienie rysunków

Wiele zadań zawiera rysunki pomocnicze. Naucz się je czytać i interpretować. Często rysunek pokazuje, która linia jest podstawą, która wysokością, jakie figury tworzą całość. Jeśli rysunek nie jest podany, warto go sobie samemu narysować, co często pomaga w uporządkowaniu informacji.

Analiza błędów

Nie zrażaj się, gdy popełniasz błędy. Analiza popełnionych błędów jest niezwykle ważnym etapem nauki. Zrozum, dlaczego dany krok był nieprawidłowy, czy był to błąd rachunkowy, czy błąd w zastosowaniu wzoru, czy może niezrozumienie treści zadania.

Praca w grupie i konsultacje

Uczenie się w grupie może być bardzo efektywne. Wspólne rozwiązywanie zadań, dyskusja nad trudniejszymi zagadnieniami, tłumaczenie sobie wzajemnie – to wszystko pomaga utrwalić wiedzę. Nie bój się również pytać nauczyciela o rzeczy, których nie rozumiesz.

Praktyczne zastosowania pola figur płaskich

Umiejętność obliczania pola figur płaskich to nie tylko szkolny wymóg, ale również praktyczna umiejętność przydatna w wielu aspektach życia. Gdzie możemy ją wykorzystać?

• Projektowanie i remonty: Planując malowanie ścian, układanie płytek, kupując dywan czy wykładzinę, musimy wiedzieć, jaką powierzchnię mamy do pokrycia. Znajomość pola prostokątów (ściany, podłoga), kwadratów czy nawet bardziej złożonych kształtów jest tu niezbędna.
• Ogrodnictwo: Przygotowując rabatę kwiatową, planując trawnik, czy obliczając ilość nawozu potrzebnego na określoną powierzchnię, posługujemy się polami figur płaskich.
• Sztuka i rzemiosło: Tworząc mozaiki, patchworki, projektując ubrania czy meble, często operujemy na płaskich kształtach i ich polach.
• Logistyka i planowanie przestrzeni: Pakując przedmioty do pudeł, układając meble w pokoju, czy planując rozmieszczenie obiektów na mapie, intuicyjnie stosujemy zasady dotyczące zajmowanej powierzchni.
• Zrozumienie świata: Nawet proste zadania, jak obliczenie pola serwetki, czy powierzchni kawałka pizzy, opierają się na tej samej wiedzy.

Wyobraźmy sobie sytuację kupna działki budowlanej. Cena często zależy od jej powierzchni. Znajomość pola kwadratu czy prostokąta pozwala nam szybko oszacować, ile będziemy musieli zapłacić. Albo planowanie kupna nowych mebli do salonu – musimy wiedzieć, czy nowy narożnik zmieści się w wyznaczonej przestrzeni, co wymaga porównania jego gabarytów z polem dostępnego miejsca.

W kontekście edukacyjnym, sprawdzian z pola figur płaskich ma na celu nie tylko sprawdzenie pamięciowego opanowania wzorów, ale przede wszystkim umiejętności analitycznego myślenia, stosowania wiedzy w praktyce i rozwiązywania problemów. Jest to fundament do dalszej nauki matematyki, zwłaszcza geometrii przestrzennej.

Podsumowanie

Sprawdzian z pola figur płaskich to ważny etap nauki matematyki w gimnazjum. Skupia się na podstawowych figurach: kwadracie, prostokącie, trójkącie, równoległoboku, trapezie i kole, wymagając znajomości odpowiednich wzorów i umiejętności ich zastosowania. Zadania mogą być zarówno proste, jak i złożone, często wymagające połączenia kilku figur lub wyznaczenia nieznanych wymiarów.

Kluczem do sukcesu jest systematyczne powtarzanie wzorów, rozwiązywanie dużej liczby zadań, analiza rysunków oraz praca nad własnymi błędami. Pamiętajmy, że umiejętność obliczania pola figur płaskich ma liczne zastosowania praktyczne w życiu codziennym, od remontów po planowanie przestrzeni.

Traktuj sprawdzian nie jako zagrożenie, ale jako możliwość sprawdzenia i utrwalenia wiedzy. Odpowiednie przygotowanie i pozytywne nastawienie z pewnością zaowocują dobrym wynikiem.