Sprawdzian Po Piątej Klasie Z Matematyki
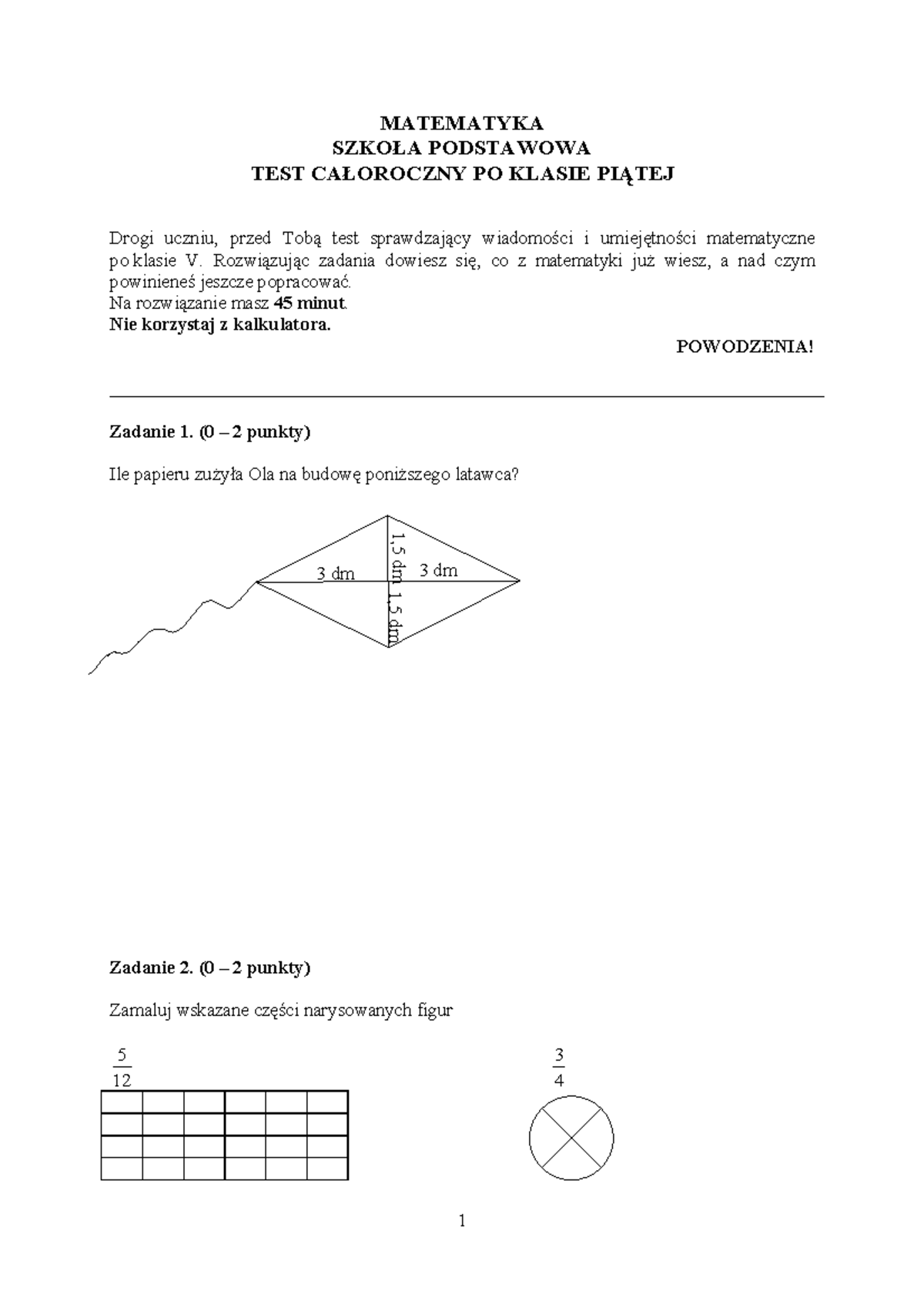
Sprawdzian po piątej klasie z matematyki to specjalny rodzaj testu, który podsumowuje i ocenia wiedzę oraz umiejętności uczniów zdobyte w ciągu całej piątej klasy szkoły podstawowej. Jest to ważne narzędzie diagnostyczne, pozwalające zarówno uczniom, jak i nauczycielom, zrozumieć poziom opanowania materiału i zidentyfikować obszary wymagające dalszej pracy.
Jak działa sprawdzian?
Krok 1: Zrozumienie zakresu materiału. Sprawdzian obejmuje kluczowe tematy nauczane w piątej klasie. Do najczęściej poruszanych zagadnień należą:
- Liczby naturalne i ułamki: działania na liczbach, porównywanie, zapis ułamków zwykłych i dziesiętnych.
- Geometria: figury płaskie, pole i obwód, kąty, bryły.
- Prawdopodobieństwo i statystyka: podstawowe pojęcia, odczytywanie danych z tabel i wykresów.
- Zadania tekstowe: rozwiązywanie problemów wymagających zastosowania różnych operacji matematycznych.
Przykład: Uczeń może zostać poproszony o obliczenie sumy 345 + 127 lub o określenie, jaki jest obwód prostokąta o bokach długości 5 cm i 8 cm.
Krok 2: Rodzaje zadań. Sprawdziany mogą zawierać różnorodne typy zadań:
- Zadania zamknięte: wybór poprawnej odpowiedzi spośród kilku opcji (np. zadania jednokrotnego wyboru).
- Zadania otwarte: wymagające samodzielnego rozwiązania i przedstawienia pełnego toku rozumowania.
- Zadania na obliczenia: proste lub złożone działania matematyczne.
- Zadania praktyczne: odnoszące się do sytuacji z życia codziennego.
Przykład: W zadaniu zamkniętym uczeń może mieć do wyboru: "Jaki jest wynik mnożenia 15 x 4? a) 50, b) 60, c) 70". W zadaniu otwartym może być konieczne obliczenie pola trójkąta, pokazując wszystkie kroki.
Krok 3: Proces rozwiązywania. Uczeń powinien podejść do sprawdzianu ze spokojem i koncentracją. Ważne jest:
- Dokładne czytanie poleceń: zrozumienie, co jest wymagane w każdym zadaniu.
- Systematyczne rozwiązywanie: przechodzenie przez zadania krok po kroku, nie pomijając żadnych etapów.
- Sprawdzanie wyników: jeśli czas pozwoli, warto wrócić do rozwiązanych zadań i zweryfikować poprawność obliczeń i odpowiedzi.
Przykład: Rozwiązując zadanie tekstowe o zakupach, należy najpierw ustalić, co jest dane, co należy obliczyć, a następnie wykonać odpowiednie działania, pamiętając o jednostkach.
Krok 4: Ocena i wnioski. Po rozwiązaniu sprawdzianu, nauczyciel ocenia pracę ucznia. Wyniki pozwalają na:
- Określenie poziomu opanowania materiału: czy uczeń osiągnął zakładane cele edukacyjne.
- Identyfikację braków: zidentyfikowanie konkretnych tematów lub typów zadań, z którymi uczeń ma trudności.
- Planowanie dalszej pracy: nauczyciel może dostosować nauczanie, a uczeń zaplanować powtórki.
Przykład: Jeśli uczeń popełnia błędy w zadaniach z ułamkami dziesiętnymi, nauczyciel może przeprowadzić dodatkowe ćwiczenia z tego zakresu.
Znaczenie sprawdzianu:
Sprawdzian po piątej klasie jest niezwykle ważny, ponieważ stanowi fundament do dalszej nauki matematyki. Poprawne zrozumienie materiału z piątej klasy ułatwia przyswajanie bardziej zaawansowanych zagadnień w kolejnych latach. Ponadto, regularne sprawdziany budują pewność siebie ucznia i uczą go systematycznej pracy nad materiałem, co jest kluczową umiejętnością nie tylko w szkole, ale i w życiu.