Sprawdzian Ostrosłupy Nowa Era Technikum

Cześć Kochani! Jestem tutaj, aby pomóc Wam przygotować się do sprawdzianu z ostrosłupów z podręcznika Nowa Era Technikum. Spokojnie, ostrosłupy nie są takie straszne, gdy zrozumiemy ich podstawowe zasady. Skupimy się na kluczowych pojęciach i wzorach, które na pewno pojawią się na sprawdzianie.

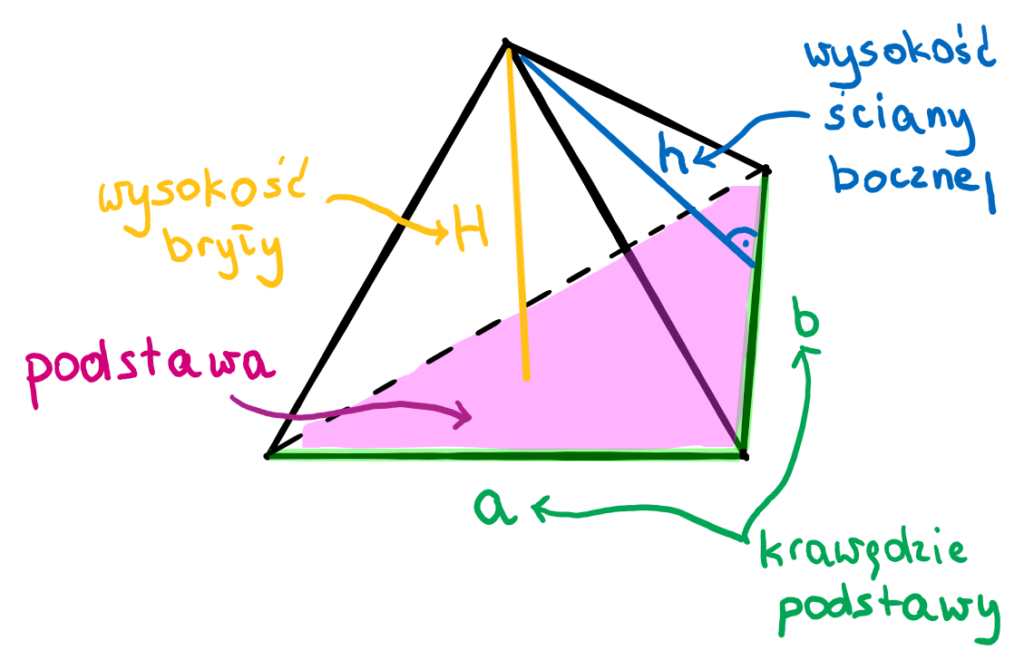
Zacznijmy od definicji. Ostrosłup to bryła geometryczna, która ma jedną podstawę (wielokąt) i ściany boczne w kształcie trójkątów, które spotykają się w jednym punkcie zwanym wierzchołkiem ostrosłupa. Pamiętajcie, że podstawa może być dowolnym wielokątem, co oznacza, że możemy mieć ostrosłupy o podstawie trójkątnej, kwadratowej, sześciokątnej i tak dalej.

Kluczowe elementy ostrosłupa to: podstawa, ściany boczne, krawędzie (podstawy i boczne) oraz wspomniany już wierzchołek. W zależności od kształtu podstawy, ostrosłupy mają swoje nazwy. Na przykład, ostrosłup o podstawie trójkątnej to ostrosłup trójkątny, a o podstawie kwadratowej to ostrosłup czworokątny.

Kolejnym ważnym pojęciem jest wysokość ostrosłupa. Jest to odcinek poprowadzony z wierzchołka ostrosłupa prostopadle do płaszczyzny podstawy. Czasami będziemy potrzebowali także wysokości ściany bocznej, która jest wysokością każdego z trójkątów tworzących ściany boczne. W przypadku ostrosłupów prawidłowych, wszystkie ściany boczne są przystającymi trójkątami równoramiennymi.

Teraz przejdźmy do wzorów. Objętość ostrosłupa (V) obliczamy za pomocą wzoru: $V = \frac{1}{3} \cdot P_p \cdot H$, gdzie $P_p$ to pole podstawy, a $H$ to wysokość ostrosłupa. To bardzo ważny wzór, który musicie zapamiętać! Bez niego trudno będzie rozwiązać większość zadań.

Powierzchnię całkowitą ostrosłupa (P_c) obliczymy, sumując pole podstawy ($P_p$) i pole wszystkich ścian bocznych ($P_b$). Czyli: $P_c = P_p + P_b$. Często pola ścian bocznych będą wymagały obliczenia pola trójkąta, gdzie potrzebna będzie wysokość ściany bocznej. Jeśli mamy ostrosłup prawidłowy, to obliczenie pola jednej ściany bocznej i pomnożenie przez liczbę ścian jest znacznie prostsze.

Przy rozwiązywaniu zadań często będziemy korzystać z twierdzenia Pitagorasa. Jest ono nieocenione przy obliczaniu wysokości, krawędzi czy apotemy (wysokości ściany bocznej), gdy znamy inne wymiary bryły. Zwracajcie uwagę na rysunki i opis zadania, aby poprawnie zidentyfikować, które odcinki są potrzebne do zastosowania twierdzenia Pitagorasa.

Szczególnym przypadkiem jest ostrosłup prawidłowy. Tutaj podstawą jest wielokąt foremny (np. kwadrat, sześciokąt), a wierzchołek znajduje się dokładnie nad środkiem podstawy. Wszystkie krawędzie boczne są równej długości, a ściany boczne to przystające trójkąty równoramienne. Zrozumienie tej specyfiki bardzo ułatwia obliczenia.

Pamiętajcie o dokładnym czytaniu poleceń i analizowaniu danych z zadania. Wizualizacja bryły i jej przekrojów również może być pomocna. Ćwiczcie na różnorodnych przykładach z podręcznika i zadań domowych, aby poczuć się pewniej.

Podsumowując kluczowe punkty:

• Ostrosłup: podstawa + trójkątne ściany boczne.
• Ważne pojęcia: podstawa, ściany boczne, krawędzie, wierzchołek, wysokość ostrosłupa, wysokość ściany bocznej.
• Objętość: $V = \frac{1}{3} \cdot P_p \cdot H$.
• Powierzchnia całkowita: $P_c = P_p + P_b$.
• Niezastąpione: twierdzenie Pitagorasa.
• Uważajcie na ostrosłupy prawidłowe – mają specjalne właściwości.