Sprawdzian Matematyka Z Plusem 3 Funkcje

Witajcie na naszym przewodniku po sprawdzianie z Funkcji z podręcznika Matematyka z Plusem 3! Ten sprawdzian może wydawać się wyzwaniem, ale z odpowiednim przygotowaniem poradzicie sobie znakomicie. Skupimy się na kluczowych zagadnieniach, które pojawią się na teście, abyście czuli się pewnie i komfortowo.

Pierwszą ważną rzeczą, o której musimy pamiętać, są **definicje funkcji**. Co to właściwie jest funkcja? Funkcja to przyporządkowanie, które każdemu elementowi z jednego zbioru (dziedziny) przyporządkowuje dokładnie jeden element z drugiego zbioru (przeciwdziedziny). Pamiętajcie, że kluczowe jest to "dokładnie jeden". Nie może być sytuacji, że jeden element z dziedziny ma przypisane dwa lub więcej elementów z przeciwdziedziny.

Kolejnym istotnym elementem są **sposoby opisywania funkcji**. Funkcje możemy opisać na kilka sposobów. Po pierwsze, możemy użyć **opisu słownego**, czyli opisać regułę słowami. Po drugie, możemy użyć **tabeli**, która pokazuje pary elementów z dziedziny i przeciwdziedziny. Po trzecie, możemy użyć **wzoru matematycznego**, czyli równania, które określa, jak wyznaczyć wartość funkcji dla danego argumentu. Wreszcie, funkcje można opisać **graficznie** za pomocą wykresu na płaszczyźnie kartezjańskiej.

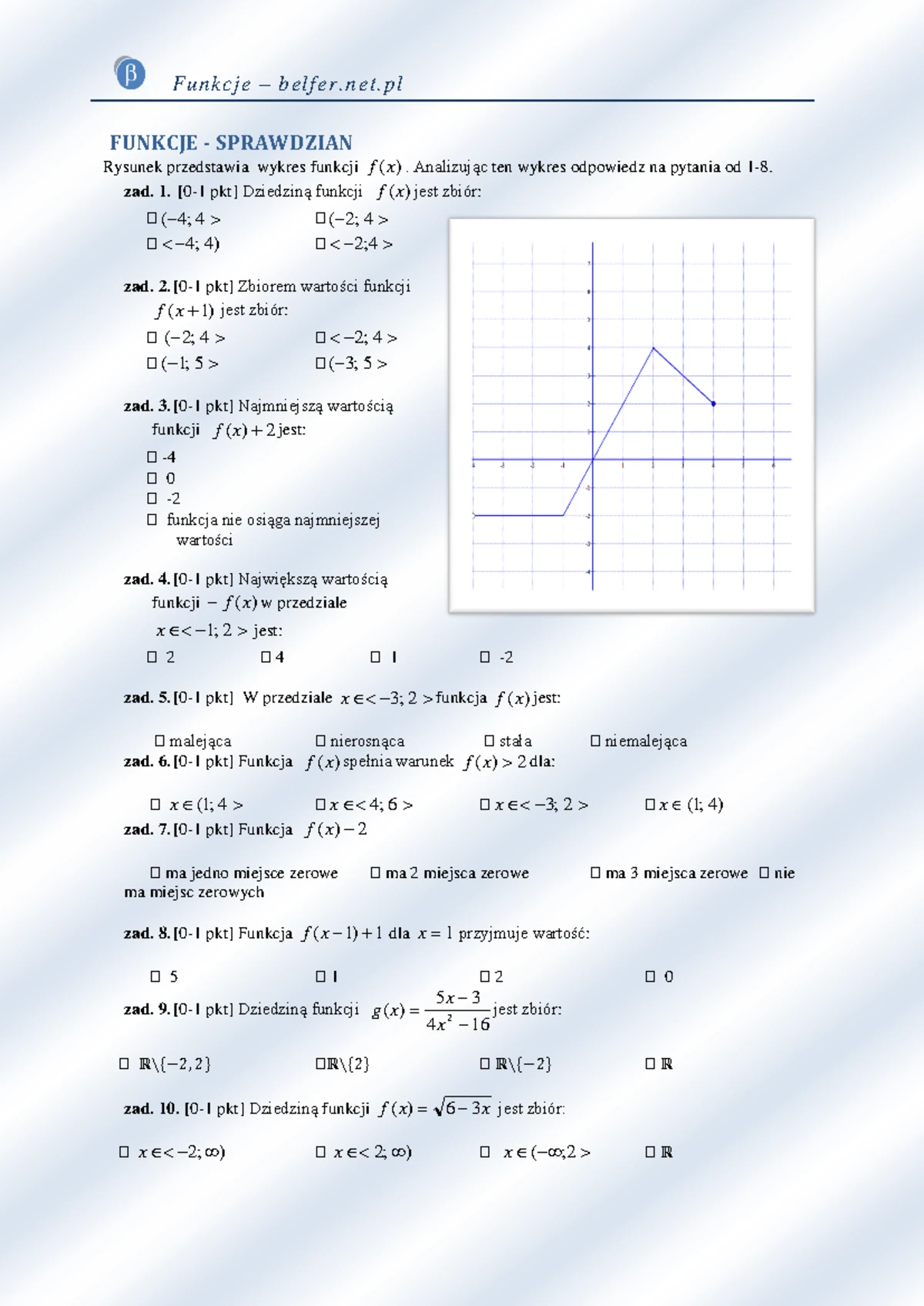
Na sprawdzianie na pewno pojawią się zadania związane z **odczytywaniem własności funkcji z wykresu**. Z wykresu funkcji możemy dowiedzieć się wielu cennych informacji. Możemy określić **dziedzinę** funkcji (wszystkie możliwe wartości x), **zbiór wartości** (wszystkie możliwe wartości y), sprawdzić, czy funkcja jest **rosnąca**, **malejąca**, czy **stała**. Z wykresu odczytamy również **miejsca zerowe** (gdzie wykres przecina oś x) oraz **wartości funkcji** dla konkretnych argumentów.

Szczególną uwagę należy zwrócić na **funkcje liniowe**. To podstawowy typ funkcji, który często pojawia się na sprawdzianach. Funkcja liniowa ma postać ogólną $y = ax + b$. Ważne jest, aby umieć zinterpretować współczynniki $a$ i $b$. **Współczynnik $a$** określa nachylenie prostej – jeśli $a > 0$, funkcja jest rosnąca, jeśli $a < 0$, jest malejąca, a jeśli $a = 0$, jest stała. **Współczynnik $b$** to wartość, którą funkcja przyjmuje dla $x=0$, czyli punkt przecięcia z osią y.

Bądźcie gotowi na zadania dotyczące **wyznaczania funkcji na podstawie danych** lub **sprawdzania, czy dany punkt należy do wykresu funkcji**. Często będziemy musieli udowodnić, że dwie funkcje są równe lub porównać ich wartości. Pamiętajcie o zastosowaniu odpowiednich wzorów i dokładności w obliczeniach.

Powodzenia na sprawdzianie! Pamiętajcie, że systematyczne powtarzanie i ćwiczenie to klucz do sukcesu. W razie wątpliwości, wróćcie do definicji i przykładów w podręczniku.

Podsumowanie kluczowych punktów:

• Definicja funkcji: przyporządkowanie, każdy element dziedziny ma dokładnie jeden element przeciwdziedziny.
• Sposoby opisu funkcji: słowny, tabelaryczny, wzorem, graficzny.
• Własności funkcji z wykresu: dziedzina, zbiór wartości, monotoniczność (rosnąca, malejąca, stała), miejsca zerowe, wartości funkcji.
• Funkcja liniowa: postać $y = ax + b$, znaczenie współczynników $a$ i $b$.
• Zadania praktyczne: wyznaczanie funkcji, sprawdzanie przynależności punktu do wykresu.