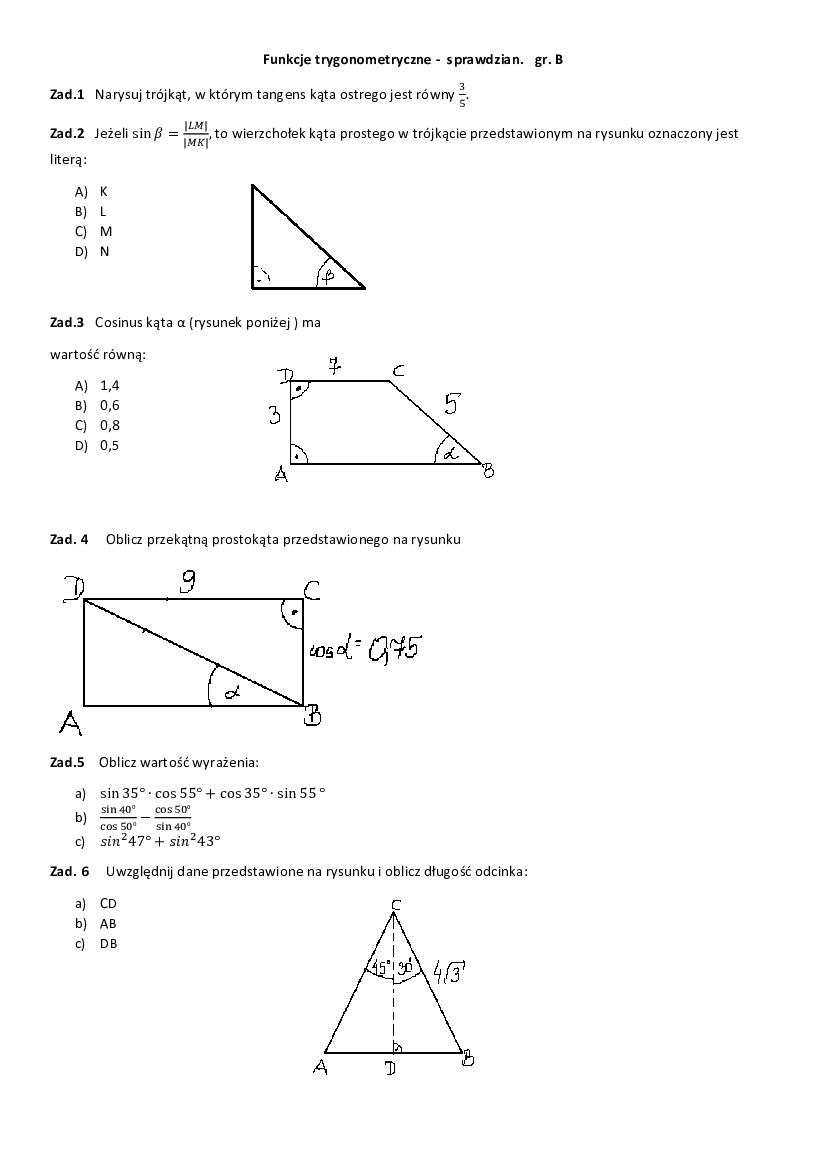
Sprawdzian Liceum Trygonometria Nowa Era

Sprawdzian z trygonometrii dla licealistów, często wydawany przez wydawnictwo Nowa Era, sprawdza zrozumienie kluczowych pojęć związanych z kątami i ich relacjami w trójkątach prostokątnych oraz poza nimi. Głównym celem jest nauczenie się opisywania zależności między bokami a kątami.
Zacznijmy od podstaw. Trygonometria to dział matematyki badający związki między kątami trójkąta a długościami jego boków. W szkole średniej zaczynamy od trójkąta prostokątnego. Jest to trójkąt, który ma jeden kąt prosty, czyli 90 stopni.
W trójkącie prostokątnym wyróżniamy trzy boki względem kąta ostrego (nie prostego), który nas interesuje:
- Przeciwprostokątna: Jest to bok leżący naprzeciwko kąta prostego. Jest zawsze najdłuższym bokiem trójkąta prostokątnego.
- Przyprostokątna przeciwległa: Jest to bok leżący naprzeciwko wybranego kąta ostrego.
- Przyprostokątna przyległa: Jest to bok leżący obok wybranego kąta ostrego, ale nie jest to przeciwprostokątna.
Na podstawie tych boków definiujemy trzy podstawowe funkcje trygonometryczne:
- Sinus (sin): Jest to stosunek długości przyprostokątnej przeciwległej do danego kąta do długości przeciwprostokątnej.
- Cosinus (cos): Jest to stosunek długości przyprostokątnej przyległej do danego kąta do długości przeciwprostokątnej.
- Tangens (tg): Jest to stosunek długości przyprostokątnej przeciwległej do danego kąta do długości przyprostokątnej przyległej do tego kąta.
Przykład: Jeśli mamy kąt α, to sin(α) = (długość przyprostokątnej przeciwległej do α) / (długość przeciwprostokątnej).
Przykład: Jeśli mamy kąt α, to cos(α) = (długość przyprostokątnej przyległej do α) / (długość przeciwprostokątnej).
Przykład: Jeśli mamy kąt α, to tg(α) = (długość przyprostokątnej przeciwległej do α) / (długość przyprostokątnej przyległej).
Ważne jest, aby pamiętać, że te definicje dotyczą kątów w trójkącie prostokątnym. Sprawdziany mogą zawierać zadania wymagające obliczenia wartości funkcji trygonometrycznych dla konkretnych kątów, na przykład 30°, 45° i 60°. Warto znać wartości tych podstawowych kątów z pamięci.
Ponadto, na sprawdzianach często pojawia się tożsamość trygonometryczna, która jest równością prawdziwą dla każdego kąta. Najważniejsza z nich to:
sin²(α) + cos²(α) = 1
Ta tożsamość mówi, że suma kwadratów sinusa i cosinusa tego samego kąta jest zawsze równa 1. Jest ona niezwykle przydatna przy rozwiązywaniu bardziej skomplikowanych zadań.
Kolejnym ważnym elementem są wartości funkcji trygonometrycznych dla kątów większych niż 90°. W tym celu wprowadza się pojęcie okręgu trygonometrycznego. Okrąg ten ma promień równy 1 i środek w początku układu współrzędnych. Kąty mierzy się od dodatniej półosi x w kierunku przeciwnym do ruchu wskazówek zegara.
- Sinus kąta na okręgu trygonometrycznym to jego współrzędna y.
- Cosinus kąta to jego współrzędna x.
- Tangens kąta można obliczyć jako iloraz sinusa przez cosinusa: tg(α) = sin(α) / cos(α).
Sprawdziany mogą również dotyczyć równań trygonometrycznych, które polegają na znalezieniu wszystkich kątów spełniających daną równość trygonometryczną. Należy wtedy pamiętać o okresowości funkcji trygonometrycznych, czyli o tym, że powtarzają się one cyklicznie.
Podsumowując, sukces na sprawdzianie z trygonometrii Nowej Ery polega na solidnym opanowaniu definicji funkcji trygonometrycznych w trójkącie prostokątnym, znajomości podstawowych wartości, rozumieniu tożsamości trygonometrycznych oraz umiejętności pracy z okręgiem trygonometrycznym i rozwiązywania podstawowych równań.