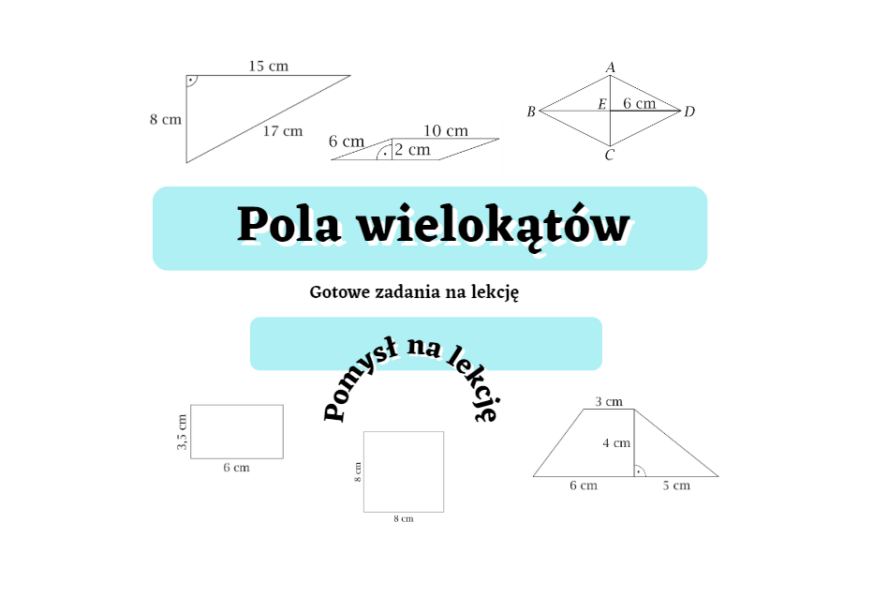
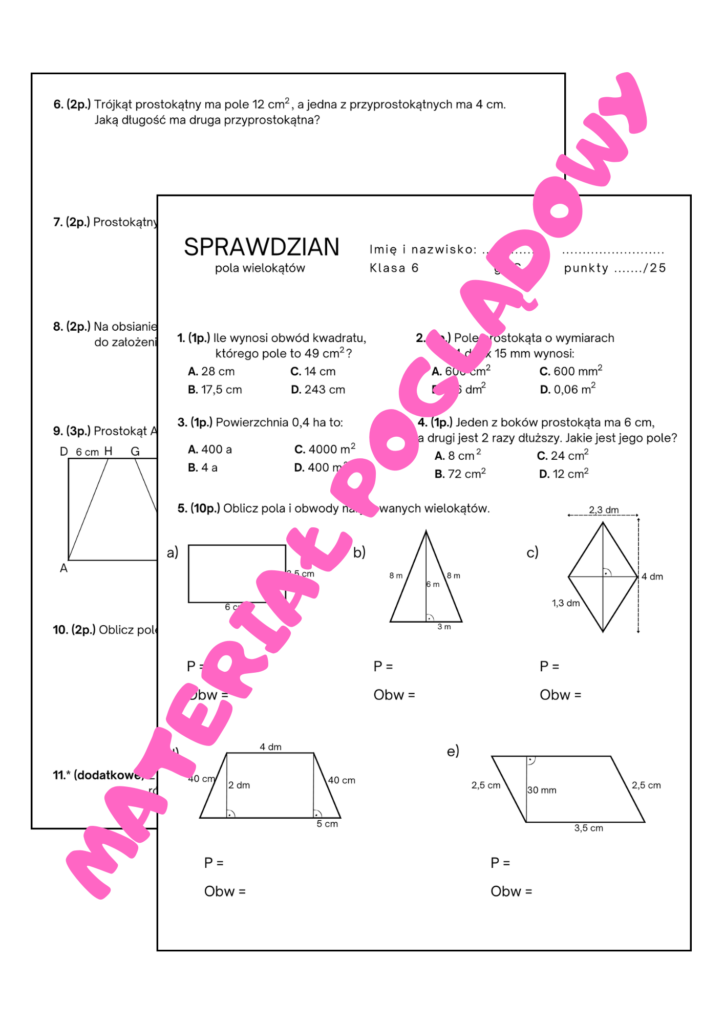
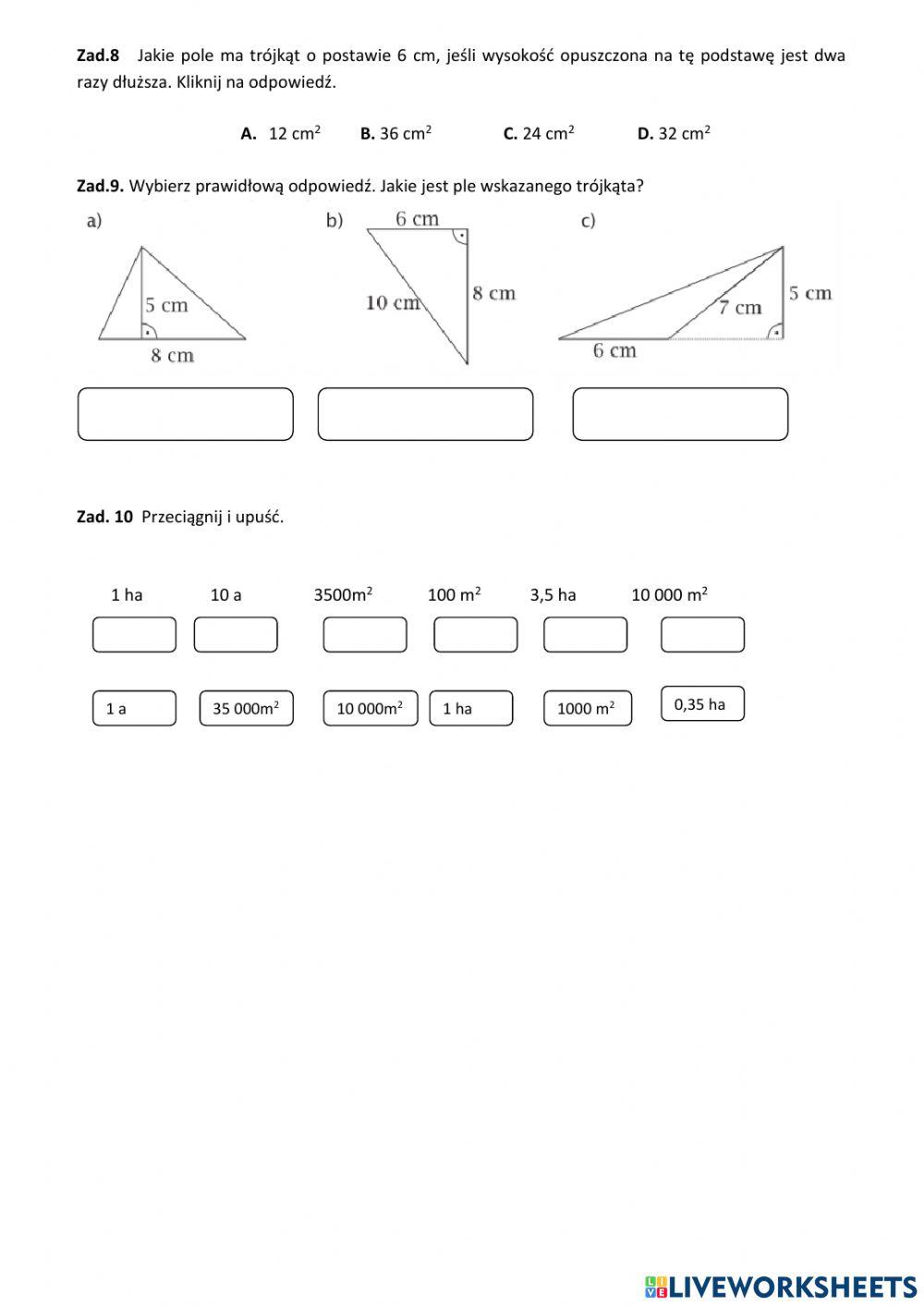
Sprawdzian Klasa 6 Pola Wielokątów Trudny

Drogi Uczniu Klasy szóstej,
Zbliża się sprawdzian z pól wielokątów. Wiem, że czasem matematyka może wydawać się trudna, a konkretne zadania spędzać sen z powiek. Ale uwierz mi, ten sprawdzian, jak każde wyzwanie, jest wspaniałą okazją do nauki i rozwoju. To nie tylko test wiedzy, ale też szansa, by pokazać sobie, jak wiele potrafisz.
Kiedy mówimy o polach wielokątów, myślimy o tym, ile miejsca zajmuje dana figura na płaszczyźnie. To jak wypełnianie pustej przestrzeni kształtami. Czy to prostokąt, trójkąt, trapez – każdy ma swoją unikalną 'powierzchnię'. A obliczanie jej to jak rozwiązywanie zagadki, gdzie kluczem są odpowiednie wzory.
Pamiętasz, jak uczyliśmy się wzoru na pole prostokąta? To proste: a * b (bok razy bok). A kwadrat? To też prostokąt, tylko jego boki są równe, więc a * a. Łatwe, prawda? Ale potem pojawiają się trójkąty. Tu jest już trochę ciekawiej. Mamy różne trójkąty: ostrokątne, prostokątne, rozwartokątne. Ale ich pole obliczamy zawsze tym samym wzorem: (podstawa * wysokość) / 2. To jest fundamentalna zasada, którą warto zapamiętać. Dlaczego tak? Wyobraź sobie, że trójkąt to połowa prostokąta. Jeśli podstawa trójkąta to jeden bok prostokąta, a wysokość to drugi, to pole prostokąta byłoby podstawa * wysokość. Ale ponieważ trójkąt to tylko połowa, dzielimy przez dwa.
A co z trapezem? To figura z dwoma równoległymi bokami, zwanymi podstawami, i pewną wysokością między nimi. Wzór na pole trapezu to: ((podstawa1 + podstawa2) * wysokość) / 2. Znowu widzimy dzielenie przez dwa, prawda? To pokazuje, że matematyka ma swoją logikę i spójność. Jeśli zrozumiesz, skąd bierze się wzór na pole trójkąta, łatwiej zrozumiesz wzór na pole trapezu.
Teraz wiem, że może pojawić się trudność, gdy kształty nie są idealne. Co jeśli mamy wielokąt złożony? Na przykład figurę, która wygląda jak dom – prostokąt z trójkątem na górze. Jak obliczyć jej pole? Tutaj wchodzi w grę strategia rozkładania. Dzielimy skomplikowany kształt na prostsze, które potrafimy już obliczyć. W naszym 'domku' obliczylibyśmy pole prostokąta, a potem pole trójkąta i dodali wyniki. To bardzo ważna umiejętność, nie tylko w matematyce, ale w całym życiu. Zamiast przytłaczać się wielkim problemem, dzielimy go na mniejsze, łatwiejsze do rozwiązania części. To jest klucz do sukcesu.
Może pojawić się też kwestia jednostek. Pamiętaj, że jeśli bok jest w centymetrach, to pole będzie w centymetrach kwadratowych (cm²). Jeśli bok jest w metrach, pole będzie w metrach kwadratowych (m²). To tak, jakbyśmy mierzyli powierzchnię kafelkami – te kafelki mają swój rozmiar, a pole to liczba kafelków, które się zmieściły.
Dlaczego to wszystko jest ważne? Bo matematyka nie kończy się na sprawdzianie. Pola wielokątów pojawiają się wszędzie wokół nas. Kiedy rodzice planują malowanie ścian, muszą wiedzieć, ile farby kupić – to powierzchnia ścian. Kiedy szyjemy ubranie, musimy wiedzieć, ile materiału potrzebujemy – to powierzchnia wykrojów. Kiedy planujemy ogród, musimy wiedzieć, ile ziemi lub trawy potrzebujemy na danym obszarze. Nawet projektanci gier komputerowych muszą wiedzieć, ile miejsca zajmują obiekty w wirtualnym świecie. To jest praktyczna matematyka, która ułatwia nam życie.
Czasem najtrudniejsze są zadania, które wymagają analizy. Nie tylko zastosowania wzoru, ale też zrozumienia, co dokładnie mamy obliczyć i jakie informacje są nam potrzebne. To jak detektywistyczna praca – szukamy wskazówek, łączymy fakty. W takich momentach ważne jest, aby nie poddawać się. Wróć do zadania, przeczytaj je jeszcze raz, może narysuj sobie pomocniczy rysunek. Czasami wystarczy spojrzeć na problem pod innym kątem.
Pamiętaj, że każdy błąd jest lekcją. Jeśli popełnisz błąd na sprawdzianie, to nie koniec świata. To informacja, nad czym jeszcze musisz popracować. Zamiast się martwić, zastanów się: co poszło nie tak? Czy zapomniałem wzoru? Czy pomyliłem się w obliczeniach? Czy źle zrozumiałem polecenie? Ta refleksja jest niezwykle cenna.
Na koniec, chciałem Cię zachęcić. Nie traktuj tego sprawdzianu jako czegoś strasznego. Traktuj go jako możliwość pokazania, jak wiele się nauczyłeś. Skup się na tym, co umiesz, przypomnij sobie wzory, przećwicz kilka przykładów. Wierzę w Ciebie. Masz w sobie siłę i potencjał, aby poradzić sobie z tym wyzwaniem. Nawet jeśli będzie trudniej, niż się spodziewasz, pamiętaj, że zdobyta wiedza i umiejętność rozwiązywania problemów zostaną z Tobą na zawsze. To jest właśnie prawdziwa wartość nauki.