Sprawdzian Graniastosłupy Klasa 6 Gdański

Rozumiemy, że dla wielu uczniów klasy szóstej, a także ich rodziców, sprawdzian z graniastosłupów może być źródłem pewnego stresu. To zupełnie naturalne – matematyka, a szczególnie geometria, czasem wydaje się abstrakcyjna i trudna do uchwycenia. Szukacie sposobu, aby nie tylko przygotować się do tego konkretnego sprawdzianu, ale także zrozumieć graniastosłupy w sposób, który będzie przydatny na dłużej, a może nawet pokaże, jak matematyka otacza nas w codziennym życiu. Ten artykuł ma na celu rozwiać Wasze wątpliwości i pokazać, że graniastosłupy to nie tylko wzory i liczby, ale fascynujący element otaczającej nas rzeczywistości.

Graniastosłupy w Codziennym Życiu: Więcej Niż Myślisz

Często, gdy słyszymy o geometrii i bryłach, wyobrażamy sobie abstrakcyjne figury z podręcznika. Jednak prawda jest taka, że graniastosłupy są wszędzie wokół nas! Zastanówcie się przez chwilę:

Pudełka na prezenty, kartony z mlekiem, opakowania od jogurtów – to wszystko są przykładami graniastosłupów prostych. Najczęściej spotykamy graniastosłupy o podstawie prostokąta, czyli prostopadłościany. Ale czy kiedykolwiek zastanawialiście się, dlaczego są one tak popularne w produkcji opakowań? Ich kształt jest optymalny do przechowywania i transportu, a jednocześnie łatwy do produkcji na skalę masową.
Budynki, zwłaszcza te starsze, często mają kształt zbliżony do graniastosłupów. Ściany są pionowe, a dach może przypominać podstawę graniastosłupa. Nawet nowoczesne budynki często wykorzystują elementy graniastosłupów, łącząc je w bardziej skomplikowane formy.
Kostki do gry – to doskonały przykład sześcianu, który jest szczególnym przypadkiem graniastosłupa, gdzie wszystkie ściany są kwadratami.
Wieże, niektóre rodzaje lamp, a nawet kawałki sera – wszystko to może przyjmować formę graniastosłupów.

Zrozumienie graniastosłupów to nie tylko ćwiczenie umysłu, ale także lepsze pojmowanie świata, który nas otacza. Kiedy widzicie pudełko, nie widzicie już tylko kartonu, ale wiecie, że to prostopadłościan, który ma określoną objętość i pole powierzchni.

Co Właściwie Jest Tym Graniastosłupem? Kluczowe Pojęcia

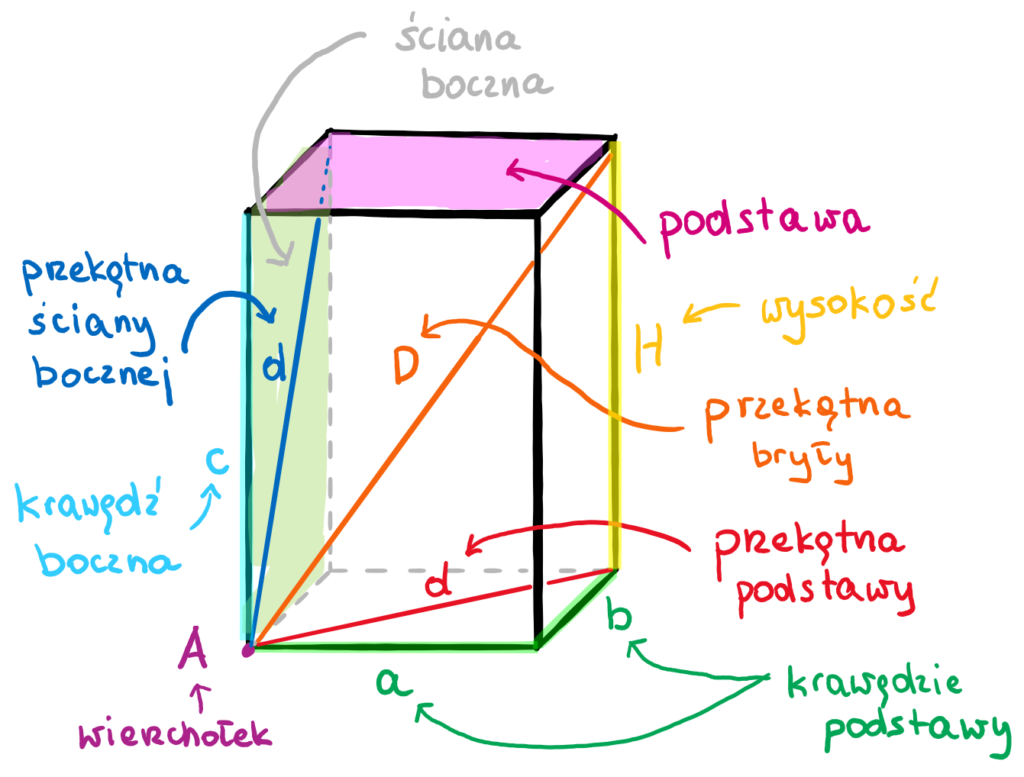
Zanim zagłębimy się w szczegóły sprawdzianu, przypomnijmy sobie podstawowe definicje. Graniastosłup to taka bryła, która ma:

Dwie równoległe i przystające podstawy. Te podstawy mogą być dowolnymi wielokątami – trójkątami, czworokątami (kwadratami, prostokątami), pięciokątami, sześciokątami i tak dalej. To od kształtu podstawy zależy nazwa graniastosłupa, np. graniastosłup trójkątny, graniastosłup sześciokątny.
Ściany boczne. Są to czworokąty (zazwyczaj prostokąty lub równoległoboki), które łączą ze sobą boki podstaw.

Ważne jest rozróżnienie między graniastosłupem prostym a ukośnym. W graniastosłupie prostym ściany boczne są prostopadłe do podstaw. To właśnie graniastosłupy proste, zwłaszcza prostopadłościany i sześciany, są najczęściej pojawiające się na sprawdzianach w klasie szóstej.

Pole Powierzchni Graniastosłupa: Suma Wszystkich Scianek

Kiedy mówimy o polu powierzchni graniastosłupa, mamy na myśli sumę pól wszystkich jego ścian – zarówno podstaw, jak i ścian bocznych. Aby to obliczyć, musimy:

Obliczyć pole jednej podstawy.
Pomnożyć je przez dwa, aby uzyskać pole obu podstaw.
Obliczyć pole każdej ze ścian bocznych.
Zsumować pola wszystkich ścian bocznych.
Na koniec dodać pole obu podstaw do sumy pól ścian bocznych.

Jest na to jednak prostszy sposób, zwłaszcza dla graniastosłupów prostych. Wtedy ściany boczne to prostokąty. Ich pole to suma pól tych prostokątów. Możemy też obliczyć obwód podstawy i pomnożyć go przez wysokość graniastosłupa (czyli odległość między podstawami). Wynik to pole powierzchni bocznej. Następnie dodajemy do tego pola dwóch podstaw.

Wzór ogólny na pole powierzchni całkowitej (Pc) graniastosłupa prostego wygląda tak: Pc = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.

Przykład: Wyobraźcie sobie pudełko po butach, które jest prostopadłościanem. Aby obliczyć jego pole powierzchni, musielibyście zmierzyć długość, szerokość i wysokość. Następnie obliczyć pole każdej z sześciu ścian i je zsumować. Alternatywnie, można obliczyć pole dna (długość razy szerokość), pole dwóch ścian bocznych (długość razy wysokość) i pole dwóch pozostałych ścian bocznych (szerokość razy wysokość), a następnie wszystko dodać.

Objętość Graniastosłupa: Ile Się Zmieści W Środku?

Objętość graniastosłupa to miara przestrzeni, którą zajmuje ta bryła. W kontekście klasy szóstej, najczęściej mamy do czynienia z obliczaniem objętości graniastosłupów prostych. Wzór jest stosunkowo prosty i intuicyjny:

V = Pp * H

Gdzie:

V to objętość
Pp to pole podstawy
H to wysokość graniastosłupa

To oznacza, że aby obliczyć objętość, wystarczy znać pole powierzchni podstawy i wysokość bryły. Jest to kluczowe pojęcie, które ma zastosowanie w wielu praktycznych sytuacjach:

Ile piasku zmieści się w wiaderku o kształcie graniastosłupa?
Ile wody można wlać do akwarium w kształcie prostopadłościanu?
Ile litrów soku znajduje się w kartoniku?

Przykład: Mamy kartonik mleka w kształcie prostopadłościanu o wymiarach 7 cm x 7 cm x 10 cm. Podstawa to kwadrat o boku 7 cm. Pole podstawy wynosi 7 cm * 7 cm = 49 cm kwadratowych. Wysokość to 10 cm. Objętość kartonika to 49 cm kwadratowych * 10 cm = 490 cm sześciennych. Ponieważ 1 cm sześcienny to 1 mililitr, nasz kartonik ma objętość 490 ml, czyli prawie pół litra!

Perspektywy Uczniów i Wyzwania

Wiemy, że wielu uczniów może czuć się przytłoczonych liczbą wzorów i kroków potrzebnych do rozwiązania zadań. Pojawiają się pytania: "Po co mi to?", "Czy ja naprawdę muszę to umieć?". To zrozumiałe, kiedy matematyka wydaje się oderwana od życia. Jednak jak pokazaliśmy, graniastosłupy są wszechobecne.

Istnieją również głosy, że zbyt duży nacisk kładzie się na zapamiętywanie wzorów, zamiast na rozwijanie intuicji geometrycznej. Zgadzamy się, że rozumienie jest kluczem. Dlatego warto nie tylko uczyć się wzorów na pamięć, ale także starać się zrozumieć, skąd się biorą i dlaczego działają. Wizualizacja brył, rysowanie ich, a nawet tworzenie własnych modeli z papieru czy klocków może bardzo pomóc w zrozumieniu przestrzeni i relacji między poszczególnymi elementami graniastosłupa.

Kolejnym wyzwaniem jest właściwe interpretowanie poleceń i danych w zadaniach. Czasami zadanie może wydawać się skomplikowane, ale często wystarczy uważnie przeczytać treść, zidentyfikować dane i szukać ukrytych informacji. Na przykład, jeśli zadanie mówi o "pudełku", zazwyczaj oznacza to prostopadłościan, chyba że podano inaczej.

Skuteczne Metody Przygotowania do Sprawdzianu

Jak zatem najlepiej przygotować się do sprawdzianu z graniastosłupów? Oto kilka sprawdzonych metod:

Powtórz definicje i wzory. Upewnij się, że rozumiesz, czym jest podstawa, ściana boczna, wysokość, pole powierzchni i objętość. Zapisz wzory w widocznym miejscu.
Ćwicz, ćwicz i jeszcze raz ćwicz! Rozwiązywanie zadań z podręcznika, zeszytu ćwiczeń, a także dodatkowych materiałów jest kluczowe. Zacznij od prostszych zadań, stopniowo przechodząc do trudniejszych.
Wizualizuj bryły. Staraj się wyobrażać sobie graniastosłupy w przestrzeni. Rysuj je, opisuj ich elementy. Jeśli to możliwe, używaj modeli brył.
Zwracaj uwagę na jednostki. Pamiętaj o poprawnym zapisywaniu jednostek (cm, m, cm², m³, cm³, m³). To często błąd, który obniża punkty.
Analizuj przykłady z życia. Gdy widzisz przedmiot, który przypomina graniastosłup, spróbuj oszacować jego wymiary i obliczyć pole powierzchni lub objętość. To świetna praktyka!
Nie bój się pytać. Jeśli czegoś nie rozumiesz, zapytaj nauczyciela, kolegę lub rodzica. Lepiej wyjaśnić wątpliwości wcześniej niż popełnić błąd na sprawdzianie.
Pracuj z rodzicami. Rodzice mogą pomóc w powtórce materiału, sprawdzaniu zadań, a także stworzeniu przyjaznej atmosfery do nauki, wolnej od presji.

Pamiętajcie, że sprawdzian to tylko jeden element Waszej edukacji. Najważniejsze jest zdobywanie wiedzy i rozumienie materiału. Nawet jeśli na sprawdzianie nie pójdzie idealnie, to zdobyte umiejętności przydadzą się Wam w przyszłości.

Gdzie Można Znaleźć Dodatkowe Materiały?

Jeśli potrzebujecie więcej ćwiczeń lub wyjaśnień, warto skorzystać z:

Podręczników i zeszytów ćwiczeń, które są zgodne z programem nauczania.
Stron internetowych z materiałami edukacyjnymi – istnieje wiele platform oferujących darmowe zadania i lekcje online.
Kanałów edukacyjnych na YouTube, gdzie często można znaleźć przystępne wyjaśnienia zagadnień matematycznych.
Biblioteki szkolnej lub lokalnej, gdzie znajdziecie dodatkowe pozycje o tematyce matematycznej.

Ważne jest, aby znaleźć materiały, które odpowiadają Waszemu stylowi nauki. Niektórzy wolą czytać, inni oglądać filmy, a jeszcze inni uczyć się przez działanie.

Podsumowanie i Kolejne Kroki

Graniastosłupy w klasie szóstej to ważny etap w nauce geometrii. Choć początkowo mogą wydawać się skomplikowane, ich zrozumienie otwiera drzwi do lepszego pojmowania otaczającego nas świata. Pamiętajcie, że kluczem jest praktyka i systematyczność. Nie chodzi o to, aby zapamiętać wszystko na pamięć, ale aby zrozumieć logikę stojącą za wzorami i zasadami.

W obliczu zbliżającego się sprawdzianu, zachęcamy Was do spokojnego podejścia. Potraktujcie to jako okazję do sprawdzenia swojej wiedzy i zidentyfikowania obszarów, które wymagają jeszcze pracy. Pamiętajcie o zastosowaniach graniastosłupów w życiu codziennym – to często najlepsza motywacja do nauki.

Jakie zadanie dotyczące graniastosłupów sprawia Wam największą trudność? Czy jest jakiś konkretny aspekt, który chciałibyście lepiej zrozumieć? Podzielcie się swoimi przemyśleniami w komentarzach lub omówcie je z nauczycielem – wspólne rozwiązywanie problemów często przynosi najlepsze efekty!