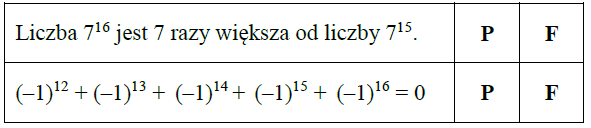Sprawdzian Gimnazjalny Z Matematyki 2017

Pamiętacie ten moment? Nerwowe spojrzenia na zegarek, szelest kartek, gorączkowe próby przypomnienia sobie tego jednego wzoru, który wydawał się taki oczywisty jeszcze kilka dni temu. Sprawdzian Gimnazjalny z Matematyki 2017 – dla wielu z Was to wciąż żywe wspomnienie, pełne emocji, wysiłku, a czasem i niedowierzania. Czy można było podejść do tego wyzwania inaczej? Czy dzisiejsi ósmoklasiści, stojący przed podobnymi egzaminami, mogą uczyć się na doświadczeniach Waszych pokoleń?

Matematyka, choć dla niektórych bywa źródłem stresu, jest kluczowym narzędziem w rozumieniu świata. To język logiki, pozwalający nam analizować dane, rozwiązywać problemy i podejmować świadome decyzje. Egzaminy, takie jak ten z 2017 roku, miały na celu sprawdzenie opanowania tych fundamentalnych umiejętności.

W tym artykule przyjrzymy się bliżej Sprawdzianowi Gimnazjalnemu z Matematyki 2017. Nie tylko omówimy jego strukturę i typowe zadania, ale przede wszystkim spróbujemy wydobyć z tego doświadczenia cenne lekcje, które mogą pomóc zarówno uczniom, jak i nauczycielom w lepszym przygotowaniu do przyszłych wyzwań. Skupimy się na aspektach, które sprawiały trudność, ale także na tych, które stanowiły dowód solidnego przygotowania. Pragniemy, aby ten tekst był nie tylko analizą przeszłości, ale także inspiracją i praktycznym przewodnikiem na przyszłość.

Analiza Struktury i Poziomu Trudności Egzaminu z 2017 Roku

Sprawdzian z 2017 roku, podobnie jak jego poprzednicy i następcy, składał się z dwóch głównych części: zadań zamkniętych i otwartych. Ta dwoistość miała na celu ocenę zarówno umiejętności szybkiego wyboru poprawnej odpowiedzi spośród kilku wariantów, jak i zdolności do samodzielnego formułowania rozwiązań i prezentowania toku rozumowania.

Zadania Zamknięte: Pułapki i Strategie

Zadania zamknięte często sprawiały uczniom najwięcej kłopotu ze względu na konieczność precyzyjnego obliczenia wyniku i prawidłowego zaznaczenia opcji. Wśród nich można było znaleźć:

Zadania testowe: Wymagały wyboru jednej poprawnej odpowiedzi spośród czterech proponowanych. Często zawierały elementy testujące rozumienie definicji, własności figur geometrycznych czy zasad działania potęg i pierwiastków.
Zadania typu "prawda-fałsz": Choć pozornie proste, potrafiły zmylić przez nieprecyzyjne sformułowania lub sytuacje brzegowe.
Zadania z luką: Wymagały wpisania poprawnego wyniku w wyznaczone miejsce. Tutaj kluczowa była dokładność obliczeń.

Jak podkreślają doświadczeni nauczyciele matematyki, na przykład Pani Anna Nowak, dyplomowany pedagog z 20-letnim stażem, "kluczem do sukcesu w zadaniach zamkniętych jest nie tylko znajomość materiału, ale także umiejętnośćstrategicznego podejścia. Należy uważnie czytać polecenia, eliminować oczywiste błędne odpowiedzi i, jeśli to możliwe, sprawdzać swój wynik". Częstym błędem było pomijanie jednostek, niepoprawne zaokrąglanie wyników lub zwykłe pomyłki rachunkowe. Badania dotyczące procesów poznawczych w rozwiązywaniu zadań matematycznych wskazują, że nawet niewielki błąd na początku obliczeń może prowadzić do błędnej odpowiedzi końcowej. Właśnie dlatego tak ważne jest metodyczne działanie.

Zadania Otwarte: Prezentacja Umiejętności

Część otwarta sprawdzianu z 2017 roku była swoistym poligonem dla uczniów, którzy musieli wykazać się nie tylko znajomością algorytmów, ale także zdolnością dologicznego myślenia i spójnego argumentowania. Zadania te można było podzielić na:

Zadania rachunkowe: Wymagały przedstawienia pełnego toku obliczeń, krok po kroku. Tutaj punktowano nie tylko ostateczny wynik, ale przede wszystkim poprawność zastosowanych metod i wykonanych działań.
Zadania geometryczne: Często dotyczyły obliczeń pól powierzchni, objętości, długości odcinków czy kątów. Ważne było poprawne zastosowanie twierdzeń, wzorów i rysunków pomocniczych.
Zadania tekstowe: Były najbardziej wymagające, ponieważ wymagały umiejętnościtłumaczenia tekstu na język matematyki. Należało zidentyfikować dane, niewiadome, zależności, a następnie sformułować równanie lub układ równań.

Pan Jan Kowalski, nauczyciel matematyki z pasją, często powtarzał swoim uczniom: "Matematyka to nie tylko liczby, to przede wszystkimsposób myślenia. Zadanie otwarte to Wasza szansa, aby pokazać, jak myślicie, jak analizujecie problem. Nie bójcie się pokazać swojego toku rozumowania, nawet jeśli nie jesteście pewni ostatecznego wyniku". Niestety, w 2017 roku wielu uczniów miało problem z tym aspektem. Część z nich popełniała błędy w zapisie algebraicznym, inni mieli trudności z doborem odpowiedniej strategii rozwiązywania, a jeszcze inni gubili się w złożoności zadań tekstowych. Badanie przeprowadzone przez Instytut Badań Edukacyjnych po egzaminach w 2017 roku wykazało, że znaczący procent uczniów miał trudności z interpretacją danych w zadaniach tekstowych i tworzeniem modeli matematycznych.

Najczęściej Pojawiające Się Zagadnienia i Typowe Błędy

Analiza arkuszy egzaminacyjnych z 2017 roku pozwala wytypować pewne obszary, które stanowiły wyzwanie dla większości uczniów. Warto zwrócić na nie szczególną uwagę, przygotowując się do przyszłych sprawdzianów.

Obszary Sprawiające Największą Trudność:

Geometria przestrzenna: Obliczanie pól powierzchni i objętości brył (stożek, walec, kula), często z wykorzystaniem twierdzenia Pitagorasa lub trygonometrii. Wiele trudności sprawiało wizualizowanie brył i wyznaczanie odpowiednich wymiarów (np. tworzącej stożka).
Zadania tekstowe z wykorzystaniem procentów i proporcji: Szczególnie te, które wymagały wieloetapowych obliczeń, takich jak obliczanie ceny po podwyżce i obniżce, lub zadania związane z czasem i prędkością.
Potęgi i pierwiastki: Choć wydawałoby się to podstawą, wielu uczniów miało problem z prawami działań na potęgach i pierwiastkach, szczególnie w bardziej złożonych wyrażeniach.
Równania i nierówności z wartością bezwzględną: Te zagadnienia często były pomijane podczas przygotowań lub źle rozumiane, co prowadziło do błędów w interpretacji graficznej lub algebraicznym rozwiązaniu.

Typowe Błędy popełniane przez Uczniów:

Na podstawie analizy prac egzaminacyjnych, można wyróżnić powtarzające się błędy:

Błędy rachunkowe: Niedokładne mnożenie, dzielenie, dodawanie czy odejmowanie – często wynikające z pośpiechu.
Błędy w zapisie algebraicznym: Niewłaściwe stosowanie reguł opuszczania nawiasów, redukcji wyrazów podobnych czy mnożenia wielomianów.
Niewłaściwe interpretowanie poleceń: Uczniowie czytali polecenia "po łebkach", nie dostrzegając kluczowych informacji, co prowadziło do rozwiązywania zupełnie innego zadania.
Brak lub niepoprawne jednostki: Zapominanie o podaniu jednostek miary w odpowiedzi, zwłaszcza w zadaniach tekstowych.
Niespójny tok rozumowania w zadaniach otwartych: Brak jasnego przedstawienia kroków prowadzących do rozwiązania, co utrudniało ocenę pracy ucznia.

Eksperci z Centralnej Komisji Egzaminacyjnej wielokrotnie podkreślali, że kluczowe jest rzetelne przygotowanie i praca nad błędami. "Każdy popełniony błąd to cenna lekcja, jeśli tylko poświęcimy czas na jego analizę i zrozumienie przyczyny" – można było usłyszeć na konferencjach dla nauczycieli. Analiza tych typowych błędów pozwala nam wskazać kierunki, w których powinny zmierzać przygotowania do egzaminu.

Praktyczne Wskazówki dla Uczniów i Nauczycieli

Jak zatem podejść do przygotowań, aby zminimalizować ryzyko popełnienia błędów i zmaksymalizować szanse na sukces? Oto kilka sprawdzonych metod i narzędzi.

Dla Uczniów:

Systematyczność to podstawa: Nie odkładaj nauki na ostatnią chwilę. Regularne powtarzanie materiału, nawet po kilkanaście minut dziennie, przyniesie lepsze efekty niż wielogodzinne "zakuwanie" przed egzaminem.
Pracuj z arkuszami z poprzednich lat: Sprawdzian Gimnazjalny z Matematyki 2017 i inne arkusze to bezcenne źródło wiedzy o tym, czego można się spodziewać. Rozwiązuj je na czas, symulując warunki egzaminacyjne.
Analizuj swoje błędy: Nie wystarczy tylko sprawdzić, czy odpowiedź jest poprawna. Spróbuj zrozumieć, dlaczego popełniłeś błąd. Czy to brak wiedzy, pomyłka rachunkowa, czy może błędna interpretacja polecenia?
Wykorzystuj różne źródła: Oprócz podręcznika i zeszytu, sięgnij po materiały online, filmy instruktażowe (np. na YouTube, gdzie wielu nauczycieli tłumaczy zagadnienia w przystępny sposób), aplikacje edukacyjne.
Zadawaj pytania: Nie bój się pytać nauczyciela, kolegów czy koleżanki, jeśli czegoś nie rozumiesz. Lepiej wyjaśnić wątpliwości od razu, niż popełnić błąd na egzaminie.
Praktykuj wizualizację: W przypadku zadań geometrycznych, rysuj diagramy, schematy. W zadaniach tekstowych, wyciągaj kluczowe dane i zapisuj je w sposób czytelny.

Dla Nauczycieli:

Budowanie solidnych fundamentów: Skupiaj się na kształtowaniu zrozumienia, a nie tylko na mechanicznym zapamiętywaniu wzorów. Pokazuj praktyczne zastosowania matematyki w życiu codziennym.
Regularne testowanie i informacja zwrotna: Krótkie kartkówki, sprawdziany w trakcie roku szkolnego pozwalają na bieżąco monitorować postępy uczniów i identyfikować obszary wymagające dopracowania. Ważne jest udzielanie szczegółowej informacji zwrotnej, wskazującej konkretne błędy.
Stosowanie różnorodnych metod nauczania: Gry edukacyjne, praca w grupach, projekty matematyczne – to wszystko może uatrakcyjnić lekcje i pomóc uczniom lepiej przyswajać wiedzę.
Przygotowanie do specyfiki egzaminu: Analiza arkuszy z poprzednich lat i informowanie uczniów o typowych strategiach rozwiązywania zadań zamkniętych i otwartych.
Wsparcie w radzeniu sobie ze stresem: Uczniowie często odczuwają silny stres przed egzaminami. Ważne jest, aby stworzyć atmosferę wsparcia, a także nauczyć uczniów technik relaksacyjnych i strategii radzenia sobie z presją.

Cytując słynnego matematyka, Carla Friedricha Gaussa: "Wiedza jest logicznym uporządkowaniem wiedzy". To zdanie doskonale oddaje istotę efektywnej nauki matematyki. Nie chodzi o zapamiętanie faktów, ale o zrozumienie zależności i struktur.

Podsumowanie: Spojrzenie w Przyszłość

Sprawdzian Gimnazjalny z Matematyki 2017 był dla wielu uczniów ważnym etapem edukacyjnym. Analizując jego specyfikę, typowe trudności i popełniane błędy, możemy wyciągnąć wnioski, które są cenne nie tylko dla tych, którzy zdawali egzamin w tamtym roku, ale przede wszystkim dla obecnych i przyszłych pokoleń ósmoklasistów. Matematyka rozwija logiczne myślenie i umiejętność rozwiązywania problemów, a te kompetencje są niezwykle ważne w XXI wieku.

Kluczem do sukcesu na egzaminie, niezależnie od roku jego przeprowadzenia, jest połączenie rzetelnej wiedzy teoretycznej z praktycznymi umiejętnościami jej stosowania. Systematyczna praca, analiza błędów, wykorzystanie różnorodnych materiałów i strategii – to wszystko składa się na efektywne przygotowanie. Pamiętajmy, że egzamin to tylko sprawdzian naszych umiejętności, a prawdziwą wartością jest wiedza i sposób myślenia, które zdobywamy po drodze.

Niech refleksja nad doświadczeniami z 2017 roku stanie się inspiracją do jeszcze lepszego przygotowania do przyszłych wyzwań. Matematyka, choć czasem trudna, może być fascynującą podróżą. Powodzenia!