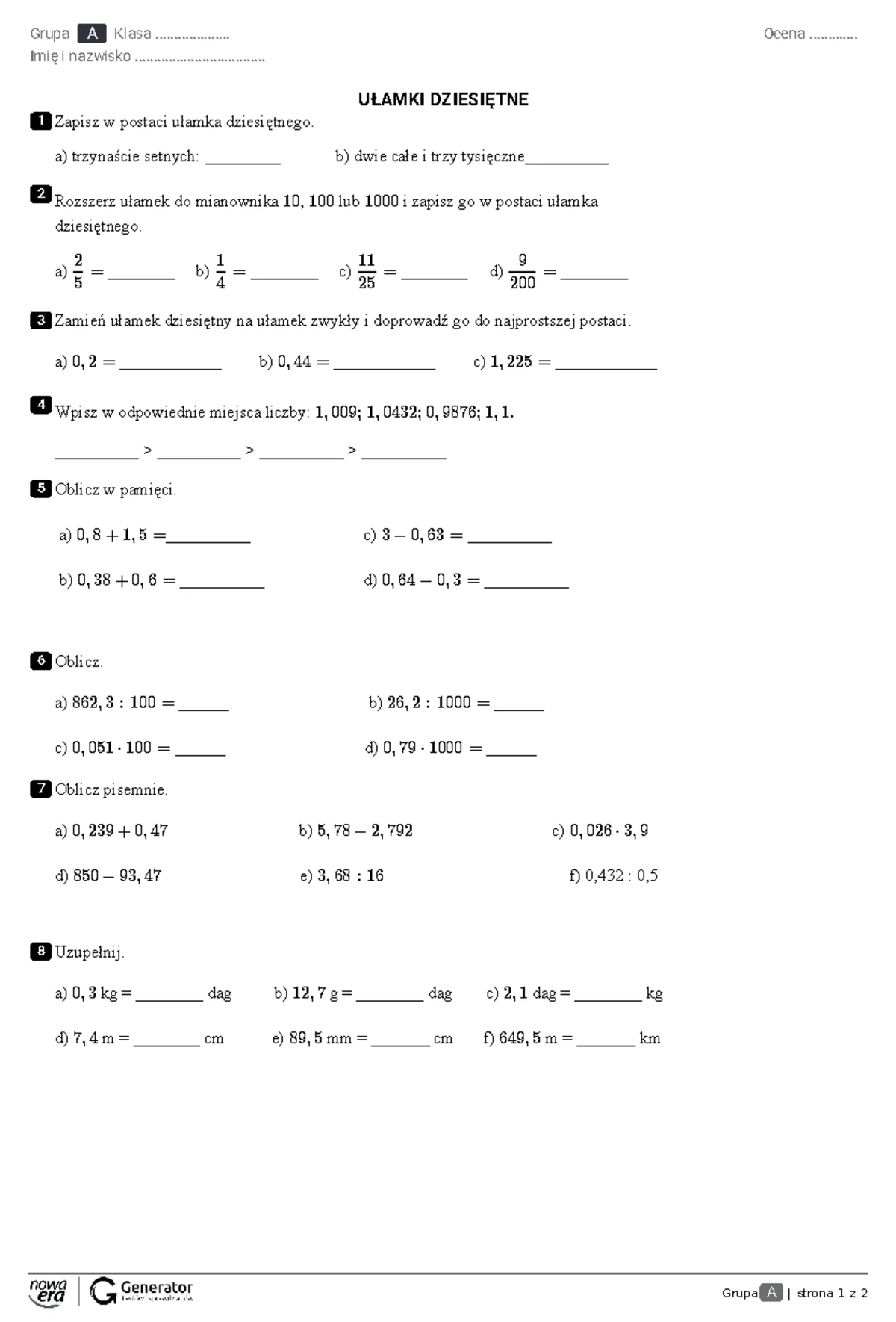
Rozwinięcia Dziesiętne Klasa 6 Sprawdzian

Rozumiemy, że temat rozwinięć dziesiętnych dla uczniów klasy szóstej może stanowić pewne wyzwanie. Pojęcie nieskończoności, zależności między ułamkami a liczbami z przecinkiem, a także operacje na tych liczbach wymagają od młodych umysłów nowego sposobu myślenia. To naturalne, że pojawiają się pytania i wątpliwości. Wiele badań edukacyjnych, na przykład tych opublikowanych w "Journal for Research in Mathematics Education", podkreśla, że uczniowie często potrzebują wizualizacji i konkretnych przykładów, aby w pełni zrozumieć abstrakcyjne koncepcje matematyczne. Celem tego artykułu jest nie tylko przygotowanie do sprawdzianu, ale przede wszystkim zbudowanie pewności siebie i głębokiego zrozumienia tego ważnego zagadnienia.

Kluczowe Zagadnienia Sprawdzianu z Rozwinięć Dziesiętnych

Sprawdzian z rozwinięć dziesiętnych zazwyczaj skupia się na kilku fundamentalnych obszarach. Zrozumienie tych obszarów to pierwszy krok do sukcesu.

1. Zrozumienie Ułamka Zwykłego i Dziesiętnego

Podstawą jest świadomość, że ułamek zwykły (np. 1/2) i ułamek dziesiętny (np. 0,5) to często ten sam fragment całości. Kluczowe jest umiejętność zamiany jednego typu ułamka na drugi.

• Zamiana z ułamka zwykłego na dziesiętny: Najprostszym sposobem jest dzielenie licznika przez mianownik. Na przykład, 3/4 to to samo co 3 podzielone przez 4, co daje 0,75. Inna metoda, szczególnie dla mianowników będących potęgami 10 (10, 100, 1000 itd.) lub które można do takich doprowadzić (np. 2 x 5 = 10), polega na rozszerzeniu ułamka. Dla 3/4, rozszerzamy do 75/100, co jest równe 0,75.
• Zamiana z ułamka dziesiętnego na zwykły: Liczbę po przecinku zapisujemy jako licznik, a jako mianownik stawiamy 1 z tyloma zerami, ile jest cyfr po przecinku. Na przykład, 0,123 to 123/1000. Jeśli to możliwe, ułamek należy skrócić.

Dlaczego to ważne? Badania pokazują, że solidne opanowanie tej konwersji jest fundamentem do dalszych działań. Bez tej umiejętności operacje na liczbach dziesiętnych stają się znacznie trudniejsze.

2. Rozwinięcia Dziesiętne Skończone i Nieskończone

Nie wszystkie ułamki zwykłe dają się zamienić na ułamki dziesiętne, które się kończą. Tutaj pojawia się pojęcie rozwinięć nieskończonych.

• Rozwinięcie skończone: Otrzymujemy je, gdy po zamianie ułamka zwykłego na dziesiętny dostajemy liczbę z końcową cyfrą. Przykłady: 1/2 = 0,5; 3/8 = 0,375; 1/10 = 0,1.
• Rozwinięcie nieskończone okresowe: Pojawia się, gdy podczas dzielenia otrzymujemy powtarzający się fragment cyfr. Ten fragment nazywamy okresem. Okres oznaczamy kropką nad pierwszą i ostatnią cyfrą okresu lub nawiasem. Przykład: 1/3 = 0,333... = 0,(3); 2/7 = 0,285714285714... = 0,(285714).

Praktyczna wskazówka: Aby sprawdzić, czy ułamek zwykły ma rozwinięcie skończone, wystarczy spojrzeć na mianownik (po uprzednim skróceniu ułamka). Jeśli mianownik po rozkładzie na czynniki pierwsze zawiera tylko dwójki i piątki, rozwinięcie będzie skończone. W przeciwnym razie będzie nieskończone okresowe.

3. Porównywanie i Uporządkowywanie Rozwinięć Dziesiętnych

To umiejętność, która wymaga precyzji. Jak porównać 0,345 z 0,35?

• Zaczynamy od porównania cyfr przed przecinkiem. Jeśli są różne, większa liczba ma większą cyfrę.
• Jeśli cyfry przed przecinkiem są takie same, przechodzimy do porównania cyfr po przecinku, zaczynając od pierwszego miejsca po przecinku.
• Porównujemy kolejne cyfry (części dziesiąte, potem setne, tysięczne itd.), aż znajdziemy miejsce, gdzie cyfry się różnią. Liczba z większą cyfrą w tym miejscu jest większa.
• Jeśli jedna liczba ma więcej cyfr po przecinku, a cyfry są identyczne do końca krótszej liczby, to ta dłuższa liczba jest większa (np. 0,5 jest mniejsze niż 0,501, bo 0,5 to 0,500).

Wskazówka dla uczniów: Aby ułatwić sobie porównywanie, można wyrównać liczbę miejsc po przecinku, dopisując zera tam, gdzie ich brakuje. Np. porównując 0,34 i 0,345, zapisujemy 0,340 i 0,345. Wtedy łatwiej dostrzec, że 0,345 jest większe.

4. Dodawanie i Odejmowanie Rozwinięć Dziesiętnych

To zadanie jest często intuicyjne dla uczniów, ponieważ przypomina dodawanie i odejmowanie liczb naturalnych, ale wymaga zachowania pionu dla przecinka.

• Upewnij się, że przecinki są wyrównane (jeden pod drugim).
• Dodawaj lub odejmuj cyfry w poszczególnych kolumnach, przenosząc w razie potrzeby, tak jak w liczbach naturalnych.
• Przecinek w wyniku musi znajdować się dokładnie pod przecinkami w liczbach, które dodajemy lub odejmujemy.

Dla rodziców i nauczycieli: Warto używać manipulacji, takich jak klocki reprezentujące dziesiątki, setki, tysięczne części. Wizualizacja tych części pomaga zrozumieć, dlaczego przecinek musi być wyrównany.

5. Mnożenie Rozwinięć Dziesiętnych

Mnożenie liczb dziesiętnych może wydawać się bardziej skomplikowane, ale opiera się na prostej zasadzie.

• Pomnóż liczby tak, jakby nie było przecinków (traktuj je jak liczby naturalne).
• Policz łącznie, ile jest cyfr po przecinku w obu mnożonych liczbach.
• W wyniku, odlicz od końca tyle miejsc po przecinku, ile wyniosła łączna liczba cyfr.

Przykład: 0,4 x 0,2. Mnożymy 4 x 2 = 8. W liczbach 0,4 i 0,2 jest łącznie dwie cyfry po przecinku. Zatem w wyniku odliczamy dwie cyfry od końca: 0,08.

Wskazówka dla uczniów: To może być dobry moment na powtórzenie tabliczki mnożenia! Im pewniej operujemy liczbami naturalnymi, tym łatwiej będzie nam radzić sobie z mnożeniem dziesiętnym.

6. Dzielenie Rozwinięć Dziesiętnych

Dzielenie może być najbardziej wymagającą operacją. Dzielimy przez dwie sytuacje: dzielenie liczby dziesiętnej przez liczbę naturalną i dzielenie liczby dziesiętnej przez liczbę dziesiętną.

• Dzielenie liczby dziesiętnej przez liczbę naturalną: Dzielimy tak, jak liczby naturalne, ale przecinek w wyniku stawiamy nad przecinkiem w dzielnej. Jeśli reszta jest różna od zera, możemy dopisać zera do dzielnej i kontynuować dzielenie.
• Dzielenie liczby dziesiętnej przez liczbę dziesiętną: Najłatwiejszym sposobem jest zamiana dzielnika na liczbę naturalną. Robimy to, przesuwając przecinek w dzielniku o tyle miejsc w prawo, ile jest cyfr po przecinku. Równocześnie musimy przesunąć przecinek w dzielnej o tyle samo miejsc w prawo. Potem dzielimy już jak w pierwszym przypadku.

Przykład: 1,2 : 0,3. Przesuwamy przecinek w 0,3 o jedno miejsce w prawo (otrzymujemy 3). Przesuwamy przecinek w 1,2 o jedno miejsce w prawo (otrzymujemy 12). Teraz dzielimy 12 : 3 = 4.

Wskazówka praktyczna: Warto poćwiczyć dzielenie z resztą oraz dzielenie "z dopisywaniem zer". Te umiejętności są kluczowe, szczególnie gdy mamy do czynienia z rozwinięciami nieskończonymi.

Przygotowanie do Sprawdzianu: Praktyczne Wskazówki

Sukces w nauce matematyki nie polega na zapamiętywaniu, ale na zrozumieniu. Oto kilka sprawdzonych strategii, które pomogą uczniom poczuć się pewnie podczas sprawdzianu.

1. Systematyczne Powtórki

Regularne ćwiczenie jest kluczem do utrwalenia wiedzy. Nie zostawiajcie powtórek na ostatnią chwilę. Kilka krótkich sesji w tygodniu jest znacznie skuteczniejsze niż jedna długa sesja tuż przed sprawdzianem.

2. Rozwiązywanie Różnorodnych Zadań

Nie ograniczajcie się do jednego typu zadań. Szukajcie zadań, które łączą różne umiejętności, np. zamianę ułamków z porównywaniem, lub dodawanie z dzieleniem. Materiały dydaktyczne często zawierają zestawy zadań o różnym poziomie trudności.

3. Wizualizacja i Konkretne Przykład

Jeśli macie trudności ze zrozumieniem, poproście o wyjaśnienie przy użyciu przykładów. Dla liczb dziesiętnych pomocne są:

• Linia liczbowa: Pokazuje położenie liczb i ich odległości.
• Modele graficzne: Kwadrat podzielony na 100 mniejszych kwadratów, gdzie zamalowanie 34 kwadratów reprezentuje 0,34.
• Pieniądze: Zrozumienie, że 1 złoty to 100 groszy, ułatwia pojęcie setnych części.

4. Szukanie Pomocy

Nie bójcie się pytać! Nauczyciel, koledzy z klasy, rodzice – każdy może pomóc. Zrozumienie wątpliwości jest pierwszym krokiem do ich rozwiązania. Nauka przez dialog jest niezwykle efektywna.

5. Techniki Zapamiętywania (jeśli potrzebne)

Dla niektórych uczniów pomocne mogą być rymowanki lub skojarzenia. Na przykład, "dwie cyfry po przecinku, czyli zawsze dzielimy przez sto".

Budowanie Pewności Siebie

Każdy sprawdzian to okazja do pokazania tego, czego się nauczyliście. Nie traktujcie go jako oceny waszej wartości, ale jako narzędzie do rozwoju. Nawet jeśli pojawią się błędy, są one cennym źródłem informacji o tym, co należy jeszcze poćwiczyć.

Pamiętajcie: Matematyka to nie tylko liczby i wzory, to także logiczne myślenie i rozwiązywanie problemów. Rozwinięcia dziesiętne, choć początkowo mogą wydawać się skomplikowane, są fascynującym mostem między światem ułamków a liczbami, które widzimy na co dzień. Z właściwym podejściem, systematyczną pracą i odrobiną cierpliwości, każdy uczeń klasy szóstej może opanować ten temat i poczuć się pewnie podczas sprawdzianu. Wierzymy w Wasze możliwości!