Prąd Gimnazjum Bryły Obrotowe Sprawdzian

Temat brył obrotowych w gimnazjum może stanowić wyzwanie, ale z odpowiednim podejściem staje się zrozumiały i fascynujący dla uczniów. Kluczem jest wizualizacja i powiązanie z otaczającym światem.

Zacznijmy od podstaw. Bryła obrotowa powstaje przez obrót płaskiej figury geometrycznej wokół prostej nazywanej osią obrotu. Wyobraźmy sobie to jako rzeźbienie w przestrzeni. Najpopularniejsze bryły to walec, stożek i kula. Każda z nich ma unikalne właściwości i wzory, które będziemy eksplorować.

Jak wytłumaczyć to uczniom w sposób zrozumiały? Używajmy prostych, analogii z życia codziennego. Walec to jak puszka konserwowa, kubek czy rolka papieru toaletowego. Stożek przypomina kapelusz czarodzieja, lody w wafelku, czy pachołek drogowy. Kula to nic innego jak piłka do gry, jabłko czy bańka mydlana.

Podczas lekcji warto korzystać z pomocy wizualnych. Modele brył obrotowych są niezwykle pomocne. Możemy je kupić lub, co ciekawsze, zrobić je wspólnie z uczniami. Przygotowanie ich z kartonu, plasteliny, a nawet z użyciem darmowych programów do projektowania 3D, może znacznie ułatwić zrozumienie przestrzennego charakteru tych figur.

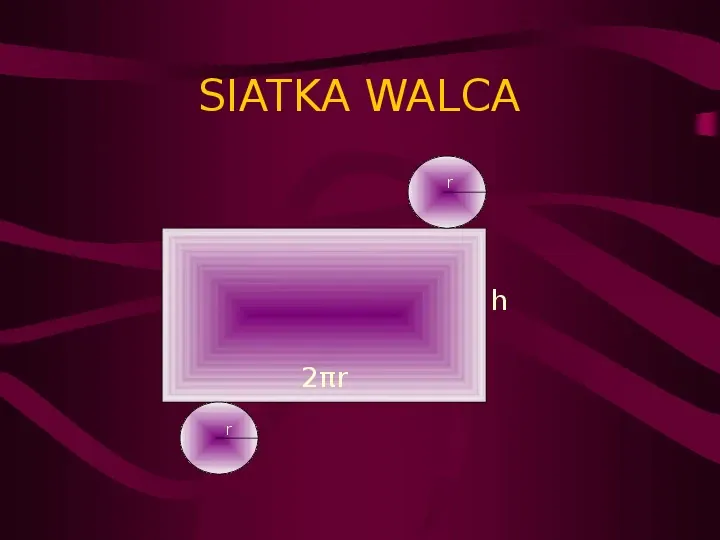
Kluczowe dla uczniów jest zrozumienie, jak konkretna figura płaska (np. prostokąt, trójkąt prostokątny, koło) generuje daną bryłę obrotową po obrocie wokół osi. Pokazanie tego na przykładzie, rysując na tablicy lub na wizualizacjach interaktywnych, jest nieocenione. Na przykład, obrót prostokąta wokół jednego z boków tworzy walec. Obrót trójkąta prostokątnego wokół przyprostokątnej daje stożek. A obrót półkola wokół średnicy skutkuje powstaniem kuli.

Częste błędy uczniów dotyczą właśnie identyfikacji figury macierzystej i osi obrotu. Niektórzy mogą mieć trudność z wyobrażeniem sobie ruchu obrotowego w trzech wymiarach. Dlatego powtarzanie ćwiczeń i demonstracji jest kluczowe. Ważne jest też, aby uczniowie rozumieli, że te same bryły można uzyskać na różne sposoby, obracając różne figury wokół różnych osi (choć w programie gimnazjalnym skupiamy się na podstawowych przykładach).

Aby uczynić ten temat bardziej angażującym, możemy wprowadzić elementy zabawy i praktycznego zastosowania. Grupowanie uczniów w zespoły i zadawanie im problemów do rozwiązania, np. obliczenie objętości basenu w kształcie walca czy pojemności czapki w kształcie stożka, sprawi, że matematyka stanie się bardziej namacalna. Możemy również zachęcić uczniów do szukania przykładów brył obrotowych w ich otoczeniu i prezentowania ich na forum klasy.

Ważne jest, aby uczniowie zrozumieli nie tylko jak wyglądają bryły obrotowe, ale także potrafili obliczyć ich objętość i pole powierzchni. Wzory te, choć na początku mogą wydawać się skomplikowane, stają się logiczne, gdy połączymy je z geometrią figur płaskich, które je tworzą. Podkreślanie związku między wzorami na pola figur płaskich a wzorami na pola i objętości brył obrotowych ułatwia ich zapamiętanie.

Regularne sprawdzanie wiedzy jest nieodłącznym elementem procesu nauczania. Sprawdzian z brył obrotowych powinien zawierać zarówno zadania teoretyczne (np. zdefiniowanie figury, wskazanie figury macierzystej), jak i praktyczne (obliczenia objętości i pól). Stosowanie zróżnicowanych typów zadań pozwala na pełniejszą ocenę zrozumienia materiału przez uczniów.