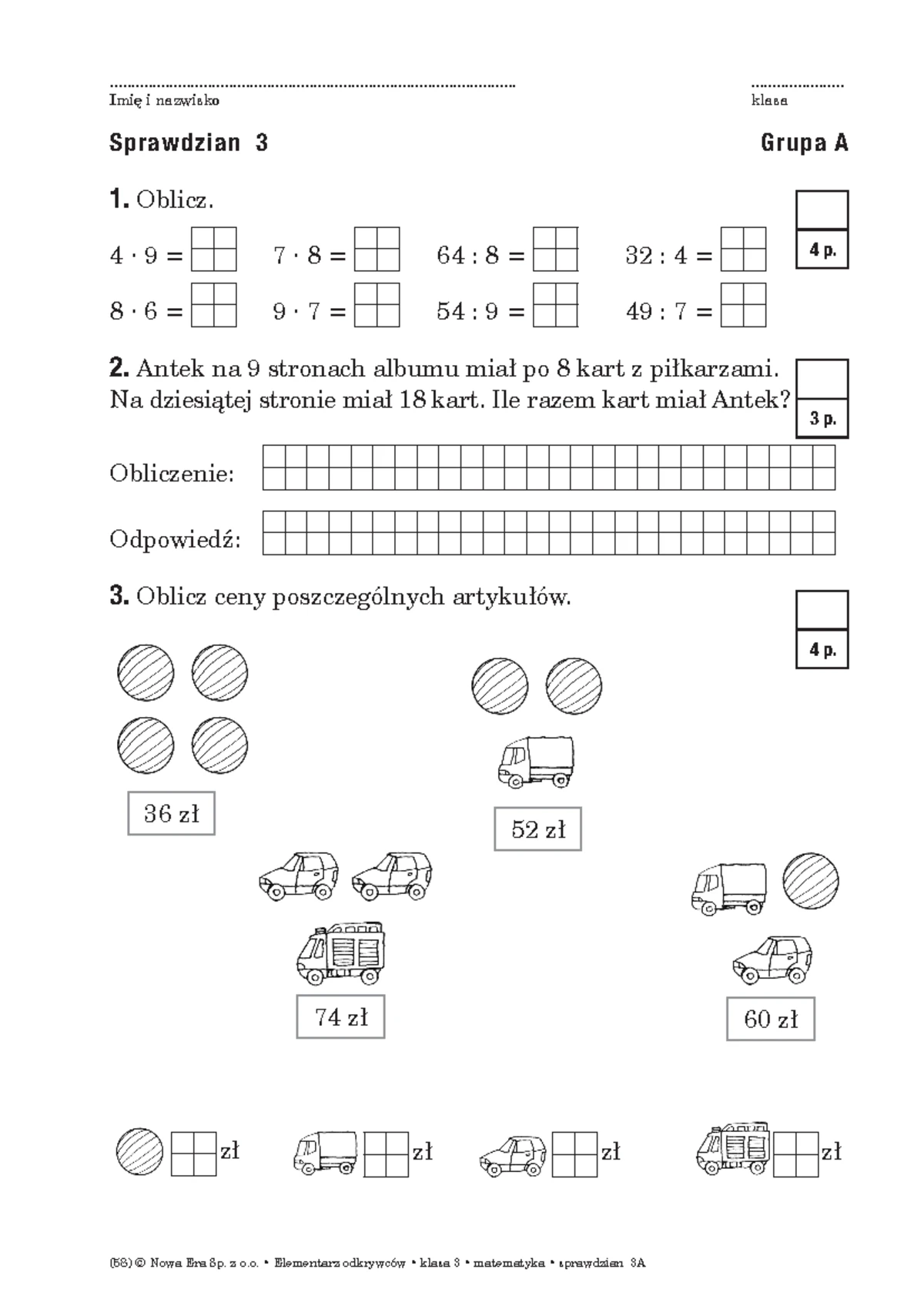
Potegi Sprawdzian Grupa A 1 Wynikiem Działania

Potęgowanie, operacja matematyczna o fundamentalnym znaczeniu, stanowi kamień węgielny wielu dziedzin nauki, techniki i życia codziennego. Zrozumienie jej mechanizmów, a przede wszystkim wyniku działania potęgi, jest kluczowe dla prawidłowego rozwiązywania zadań matematycznych, od prostych obliczeń arytmetycznych po złożone problemy w analizie matematycznej, fizyce czy informatyce. Niniejszy artykuł ma na celu dogłębne przyjrzenie się kwestii wyniku działania potęgi, analizując jego naturę, właściwości oraz praktyczne zastosowania, ze szczególnym uwzględnieniem materiału, który mógłby pojawić się na sprawdzianie z potęg dla grupy A, element pierwszy.

Kiedy mówimy o wyniku działania potęgi, mamy na myśli konkretną liczbę, która powstaje w wyniku pomnożenia podstawy potęgi przez siebie tyle razy, ile wynosi wykładnik. Jest to fundamentalna definicja, która stanowi punkt wyjścia do dalszych rozważań.

Definicja i Podstawowe Właściwości Wyniku Działania Potęgi

Potęga jest zapisem skróconego mnożenia. Forma ogólna potęgi to aⁿ, gdzie 'a' jest podstawą potęgi, a 'n' jest wykładnikiem. Wynikiem działania potęgi jest liczba, która powstaje w wyniku wykonania tego skróconego mnożenia. I tak na przykład, 2³ oznacza 2 * 2 * 2, a wynikiem działania potęgi jest 8.

Kluczowe jest zrozumienie, że wynik działania potęgi zależy zarówno od podstawy, jak i od wykładnika. Zmiana jednego z tych elementów prowadzi do zupełnie innej wartości końcowej.

Przypadek Wykładnika Naturalnego

Dla wykładników naturalnych (dodatnich liczb całkowitych), wynik działania potęgi jest prosty do wyznaczenia. Jest to iloczyn podstawy powtórzony tyle razy, ile wynosi wykładnik.

• Przykład: 5⁴ = 5 * 5 * 5 * 5 = 625. Tutaj 625 to wynik działania potęgi.
• Przykład: (-3)² = (-3) * (-3) = 9. Tutaj 9 to wynik działania potęgi. Zwracamy uwagę na znak wyniku.
• Przykład: (-3)³ = (-3) * (-3) * (-3) = -27. Tutaj -27 to wynik działania potęgi.

Jest to kluczowe zagadnienie, które często pojawia się na sprawdzianach – wynik działania potęgi z ujemną podstawą i parzystym wykładnikiem jest zawsze dodatni, natomiast z ujemną podstawą i nieparzystym wykładnikiem jest zawsze ujemny. To właśnie te niuanse decydują o poprawności rozwiązania.

Przypadek Wykładnika Równego Zero

Szczególnym przypadkiem jest wykładnik równy zero. Zgodnie z definicją matematyczną, dla każdej liczby różnej od zera, wynik działania potęgi o wykładniku zero jest równy 1.

• Przykład: 10⁰ = 1. Tutaj 1 to wynik działania potęgi.
• Przykład: (-7)⁰ = 1. Tutaj 1 to wynik działania potęgi.

Należy pamiętać o szczególnym przypadku: 0⁰ jest często uznawane za symbol nieoznaczony, choć w niektórych kontekstach (np. w teorii szeregów potęgowych) przyjmuje się jego wartość jako 1. Na poziomie podstawowym, zazwyczaj operujemy na liczbach rzeczywistych, gdzie a⁰ = 1 dla a ≠ 0.

Przypadek Wykładnika Ujemnego

Gdy wykładnik jest liczbą ujemną, wynik działania potęgi jest odwrotnością potęgi o wykładniku dodatnim. Czyli a^-n = 1 / aⁿ.

• Przykład: 2^-3 = 1 / 2³ = 1 / 8. Tutaj 1/8 to wynik działania potęgi.
• Przykład: (1/3)^-2 = 1 / (1/3)² = 1 / (1/9) = 9. Tutaj 9 to wynik działania potęgi.

To pozwala nam na operowanie liczbami mniejszymi od jedności w sposób uporządkowany i przewidywalny. Wynik działania potęgi z ujemnym wykładnikiem często prowadzi do ułamków, co jest naturalną konsekwencją tej operacji.

Potęgi o Wykładniku Wymiernym i Niewymiernym

Rozszerzając nasze rozumienie wyniku działania potęgi, wkraczamy w obszary wykładników wymiernych i niewymiernych.

Wykładniki Wymierne

Wykładnik wymierny, czyli liczba, którą można zapisać jako ułamek p/q, gdzie p jest liczbą całkowitą, a q jest liczbą naturalną, wiąże się z pierwiastkowaniem.

• a^p/q = ^q√a^p

Oznacza to, że wynik działania potęgi o wykładniku wymiernym jest pierwiastkiem q-tego stopnia z podstawy podniesionej do potęgi p.

• Przykład: 8^2/3 = ³√8² = ³√64 = 4. Tutaj 4 to wynik działania potęgi.
• Alternatywnie: 8^2/3 = (³√8)² = 2² = 4. Ta metoda często ułatwia obliczenia.

Zrozumienie tej zależności jest kluczowe, ponieważ pozwala przekształcić potęgi o trudnych wykładnikach na operacje pierwiastkowania, które mogą być łatwiejsze do wykonania lub wizualizacji.

Wykładniki Niewymierne

Wykładniki niewymierne, takie jak √2 czy π, są bardziej abstrakcyjne. Wynik działania potęgi z takim wykładnikiem jest zazwyczaj liczbą niewymierną i często wymaga użycia kalkulatora lub zaawansowanych metod numerycznych do przybliżonego wyznaczenia wartości.

• Przykład: 2^√2. Ten wynik jest liczbą niewymierną, trudną do precyzyjnego obliczenia ręcznie.

Dla celów sprawdzianów, zazwyczaj skupiamy się na wykładnikach naturalnych, zerowych, ujemnych i wymiernych, które pozwalają na dokładne wyznaczenie wyniku działania potęgi.

Właściwości Działania na Potęgach a Wynik

Kolejnym istotnym aspektem, który wpływa na wynik działania potęgi, są właściwości działań na potęgach, czyli reguły, które pozwalają upraszczać i przekształcać wyrażenia potęgowe.

Mnożenie Potęg o Tych Samych Podstawach

Gdy mnożymy dwie potęgi o tej samej podstawie, wynik działania potęgi jest potęgą o tej samej podstawie, a wykładnik jest sumą wykładników.

• a^m * aⁿ = a^m+n

Przykład: 3² * 3⁴ = 3²⁺⁴ = 3⁶. Tutaj 3⁶ to nasz wynik, który można dalej obliczyć.

Dzielenie Potęg o Tych Samych Podstawach

Podczas dzielenia potęg o tej samej podstawie, wynik działania potęgi jest potęgą o tej samej podstawie, a wykładnik jest różnicą wykładników.

• a^m / aⁿ = a^m-n (dla a ≠ 0)

Przykład: 7⁵ / 7² = 7^5-2 = 7³. Tutaj 7³ to wynik, który można dalej obliczyć.

Potęgowanie Potęgi

Potęgowanie potęgi prowadzi do mnożenia wykładników.

• (a^m)ⁿ = a^m*n

Przykład: (4²)³ = 4^2*3 = 4⁶. 4⁶ to wynik tej operacji.

Potęga Iloczynu i Ilorazu

Potęgowanie iloczynu i ilorazu polega na potęgowaniu każdego czynnika z osobna.

• (a * b)ⁿ = aⁿ * bⁿ
• (a / b)ⁿ = aⁿ / bⁿ (dla b ≠ 0)

Przykład: (2 * 5)³ = 2³ * 5³ = 8 * 125 = 1000. Można też obliczyć (2*5)³ = 10³ = 1000.

Te właściwości są niezastąpione podczas upraszczania skomplikowanych wyrażeń. Ich poprawne zastosowanie pozwala na szybkie i bezbłędne wyznaczenie wyniku działania potęgi w trudniejszych zadaniach.

Przykład Zastosowania na Sprawdzianie (Grupa A, Element 1)

Wyobraźmy sobie zadanie ze sprawdzianu, które brzmiałoby mniej więcej tak:

Zadanie 1: Oblicz wynik działania:

a) 3⁴ + 5²

b) (2³)² / 2⁴

c) 4^-2 * 2⁵

Rozwiązanie a):

Najpierw obliczamy poszczególne potęgi. 3⁴ to 3 * 3 * 3 * 3 = 81. Następnie 5² to 5 * 5 = 25.

Teraz dodajemy wyniki: 81 + 25 = 106. 106 to wynik działania potęgi w tym podpunkcie.

Rozwiązanie b):

Korzystamy z właściwości potęgowania potęgi: (2³)² = 2^3*2 = 2⁶.

Teraz dzielimy: 2⁶ / 2⁴ = 2^6-4 = 2².

Obliczamy ostateczny wynik działania potęgi: 2² = 4.

Rozwiązanie c):

Najpierw przekształcamy 4^-2. Możemy zapisać 4 jako 2². Zatem 4^-2 = (2²)^-2 = 2^-4.

Teraz mnożymy: 2^-4 * 2⁵ = 2^-4+5 = 2¹.

Ostateczny wynik działania potęgi to 2.

Takie zadania wymagają od ucznia nie tylko znajomości definicji, ale także umiejętności stosowania właściwości działań na potęgach. Wynik działania potęgi w każdym kroku musi być poprawnie obliczony.

Potęgi w Życiu Codziennym i Nauce

Choć na pierwszy rzut oka może się wydawać, że potęgi są domeną czystej matematyki, ich zastosowania są wszechobecne.

• Fizyka: Przy opisie dużych odległości (jednostki astronomiczne, lata świetlne), małych cząstek (rozmiary atomów), prędkości światła, czy mocy urządzeń elektrycznych często używamy notacji naukowej, która opiera się na potęgach dziesiątki (np. 3 x 10⁸ m/s dla prędkości światła).
• Informatyka: Pojemność pamięci komputerowej jest mierzona w bajtach, kilobajtach (2¹⁰ bajtów), megabajtach (2²⁰ bajtów), gigabajtach (2³⁰ bajtów) i terabajtach (2⁴⁰ bajtów). Wynik działania potęgi tutaj określa skalę i możliwości technologiczne.
• Finanse: Oprocentowanie składane, gdzie odsetki naliczane są od kapitału wraz z wcześniej naliczonymi odsetkami, jest przykładem zastosowania potęg do obliczania wzrostu kapitału w czasie.
• Biologia: Tempo wzrostu populacji organizmów, zwłaszcza w początkowej fazie rozwoju, często można opisać funkcjami wykładniczymi.

W każdym z tych przykładów, wynik działania potęgi nie jest tylko abstrakcyjną liczbą, ale konkretną wartością opisującą rzeczywiste zjawiska.

Podsumowanie i Kluczowe Wnioski

Zrozumienie wyniku działania potęgi jest fundamentalne dla sukcesu w nauce matematyki i jej praktycznych zastosowaniach. Kluczowe jest:

• Dokładne zapamiętanie definicji potęgowania dla różnych typów wykładników (naturalnych, zerowych, ujemnych, wymiernych).
• Świadomość wpływu znaku podstawy i parzystości/nieparzystości wykładnika na znak wyniku działania potęgi.
• Perfekcyjne opanowanie właściwości działań na potęgach, które umożliwiają upraszczanie wyrażeń i efektywne obliczenia.
• Umiejętność interpretacji wyniku w kontekście zadania, czy to czysto matematycznego, czy też praktycznego.

Sprawdzian z potęg, zwłaszcza jego pierwszy element, często koncentruje się na podstawach i podstawowych operacjach. Uważne przestudiowanie tych zagadnień, wraz z praktycznym rozwiązywaniem zadań, zapewni solidne fundamenty. Pamiętajmy, że każdy wynik działania potęgi jest wynikiem precyzyjnego procesu matematycznego, a jego poprawne obliczenie jest kluczem do dalszego postępu.

Zachęcamy do regularnego ćwiczenia i powtarzania materiału, aby każdy wynik działania potęgi był dla Was jasny i oczywisty. Powodzenia na sprawdzianie!