Pola Figur Płaskich Sprawdzian Gimnazjum

Witajcie przyszli mistrzowie geometrii! Dzisiaj zanurzymy się w fascynujący świat figur płaskich. Wyobraźcie sobie płaski świat, gdzie możemy rysować i mierzyć tylko na powierzchni, jak na kartce papieru. To właśnie tam żyją nasze figury płaskie!

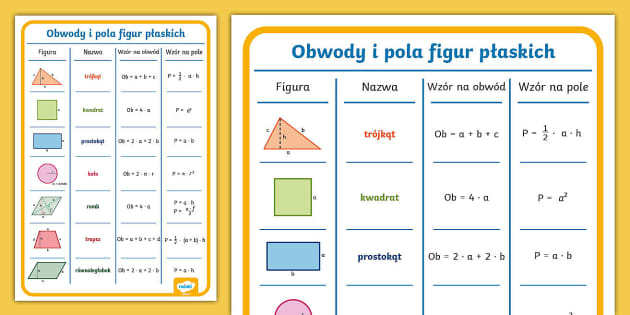
Naszym głównym bohaterem dzisiaj jest obwód. Pomyślcie o obwodzie jak o ogrodzeniu wokół Waszego ogródka. Aby zmierzyć obwód, musimy przejść się dookoła całego ogrodzenia i zsumować długość każdej jego części. Czyli to po prostu suma długości wszystkich boków figury.

Weźmy na przykład kwadrat. Ma on cztery równe boki. Wyobraźcie sobie kostkę cukru, która leży na stole – jej jedna ścianka to kwadrat. Jeśli bok kwadratu ma długość 5 cm, to obwód będzie wynosił 5 cm + 5 cm + 5 cm + 5 cm, czyli 20 cm. To tak, jakbyśmy chcieli przyciąć wstążkę, żeby otoczyć ten kwadratowy kawałek ciasta!

A co z prostokątem? Prostokąt jest jak pudełko od butów. Ma dwa dłuższe boki i dwa krótsze. Jeśli krótszy bok ma 3 cm, a dłuższy 7 cm, to aby obliczyć obwód, dodajemy: 3 cm + 7 cm + 3 cm + 7 cm. To daje nam 20 cm. Pamiętajcie, że przeciwległe boki prostokąta są sobie równe, jak dwie naprzeciwko siebie stojące ściany pokoju.

Teraz przejdźmy do czegoś okrągłego – koła. Koło jest jak tarcza zegara albo talerz. Tutaj nie mamy boków, ale mamy średnicę (linię przechodzącą przez środek koła) i promień (połowa średnicy). Obwód koła, który nazywamy długością okręgu, obliczamy przy pomocy specjalnej liczby – PI, oznaczonej grecką literą π. W przybliżeniu π ma wartość około 3,14. Długość okręgu obliczamy mnożąc średnicę przez π, albo 2 razy promień razy π. To tak, jakbyśmy chcieli otoczyć całe koło sznurkiem.

Kolejnym ważnym pojęciem jest pole. Pole to obszar, który figura zajmuje na płaszczyźnie. Wyobraźcie sobie, ile farby potrzebujecie, żeby pomalować całą ścianę. To właśnie pole! Jest to miara wnętrza figury.

Dla kwadratu pole jest bardzo proste. Mnożymy długość boku przez siebie. Jeśli bok kwadratu ma 5 cm, to pole wynosi 5 cm * 5 cm, czyli 25 cm kwadratowych (piszemy to jako 25 cm²). To tak, jakbyśmy chcieli pokryć całą kwadratową powierzchnię małymi kwadracikami o boku 1 cm.

Prostokąt też ma łatwe pole. Mnożymy długość jednego boku przez długość drugiego boku. W naszym przykładzie z prostokątem o bokach 3 cm i 7 cm, pole wynosi 3 cm * 7 cm = 21 cm². To tak, jakbyśmy chcieli ułożyć na podłodze płytki o wymiarach 1 cm na 1 cm, aby pokryć całą powierzchnię prostokątnego pokoju.

Obliczanie pola koła wymaga naszej liczby π. Pole koła to π razy promień razy promień (czyli promień do kwadratu). Jeśli promień koła ma 4 cm, to pole wynosi π * 4 cm * 4 cm, co daje nam około 3,14 * 16 cm² = 50,24 cm². Pamiętajcie, że jednostki pola zawsze są podniesione do potęgi drugiej, bo to miara dwuwymiarowa – szerokość i długość.

Pamiętajcie, że obwód to linia dookoła, a pole to przestrzeń w środku. Ćwicząc te wzory i wyobrażając sobie te porównania, staniecie się prawdziwymi ekspertami w dziedzinie figur płaskich! Powodzenia na sprawdzianie!