Pola Figur Płaskich Gimnazjum Sprawdzian

W świecie matematyki, zwłaszcza na poziomie gimnazjum, figury płaskie stanowią fundamentalny element edukacji. Ich zrozumienie otwiera drzwi do bardziej zaawansowanych koncepcji geometrycznych i jest kluczowe w wielu dziedzinach życia, od projektowania architektonicznego po analizę danych. Sprawdzian z tego zakresu to nie tylko test wiedzy, ale przede wszystkim okazja do utrwalenia umiejętności i zbudowania solidnych podstaw.

Często spotykanym wyzwaniem dla uczniów jest nie tyle samo rozpoznawanie figur, co zrozumienie ich właściwości i umiejętność stosowania odpowiednich wzorów. Sprawdziany z pola figur płaskich wymagają nie tylko pamięci, ale przede wszystkim myślenia logicznego i umiejętności rozwiązywania problemów. To właśnie te umiejętności są kształtowane podczas pracy nad zadaniami tego typu.

W dalszej części artykułu przyjrzymy się kluczowym zagadnieniom związanym ze sprawdzianem z pola figur płaskich, oferując wskazówki, przykłady i kontekst, który pomoże uczniom lepiej przygotować się do tego ważnego egzaminu. Skupimy się na praktycznym podejściu, pokazując, jak teoria przekłada się na rzeczywiste zastosowania.

Kluczowe Figury i Ich Właściwości

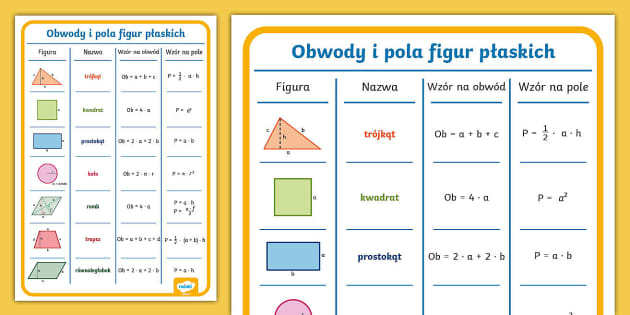
Na sprawdzianie z pola figur płaskich gimnazjaliści najczęściej spotykają się z podstawowymi kształtami: kwadratem, prostokątem, trójkątem, kołem, równoległobokiem, rombem i trapezem. Zrozumienie unikalnych cech każdej z tych figur jest absolutnie niezbędne.

Kwadrat i Prostokąt – Podstawy Wzornictwa

Kwadrat, z jego czterema równymi bokami i czterema kątami prostymi, jest figurą najprostszą do opanowania. Jego pole obliczamy ze wzoru: P = a², gdzie 'a' to długość boku.

Prostokąt, posiadający dwie pary równych boków i cztery kąty proste, jest nieco bardziej złożony, ale nadal prosty w użyciu. Wzór na jego pole to: P = a * b, gdzie 'a' i 'b' to długości sąsiednich boków. Ważne jest, aby pamiętać, że kwadrat jest szczególnym przypadkiem prostokąta.

Przykład z życia: Wyobraźmy sobie potrzebę ułożenia nowej podłogi w pokoju. Jeśli pokój ma kształt prostokąta o wymiarach 4 metry na 5 metrów, obliczenie potrzebnej ilości płytek (zakładając ich standardowy rozmiar) wymaga policzenia pola podłogi: P = 4m * 5m = 20 m².

Trójkąt – Różnorodność i Precyzja

Trójkąt, figura o trzech bokach, prezentuje większą różnorodność. W zależności od rodzaju trójkąta (różnoboczny, równoramienny, równoboczny, prostokątny), wzory na pole mogą się nieznacznie różnić, ale podstawowy i uniwersalny wzór to: P = (1/2) * a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Kluczowe jest tutaj zrozumienie pojęcia wysokości. Jest to odcinek prostopadły do podstawy (lub jej przedłużenia), łączący wierzchołek z podstawą. W przypadku trójkątów prostokątnych, przyprostokątne mogą pełnić rolę podstawy i wysokości, co upraszcza obliczenia: P = (1/2) * a * b, gdzie 'a' i 'b' to długości przyprostokątnych.

Przykład z życia: Dach domu często ma kształt trójkąta. Architekt, projektując dach, musi obliczyć jego powierzchnię, aby oszacować potrzebną ilość materiałów dachowych. Znając długość okapu (podstawa) i wysokość dachu, można obliczyć pole powierzchni dachu.

Koło – Tajemnica Liczby Pi

Koło jest figurą szczególną, definiowaną przez środek i promień. Jego pole obliczamy ze wzoru: P = π * r², gdzie 'r' to promień koła, a 'π' (pi) to stała matematyczna o przybliżonej wartości 3.14159.

Często w zadaniach podaje się średnicę (d), która jest dwukrotnością promienia (d = 2r). Wówczas promień obliczamy jako r = d/2, a wzór na pole przybiera postać: P = π * (d/2)².

Przykład z życia: Obliczanie pola powierzchni pizzy, okrągłego stołu, czy nawet koła zębatego w mechanizmie opiera się na tym wzorze. Jeśli średnica pizzy wynosi 30 cm, jej pole powierzchni można obliczyć jako: P = π * (30cm/2)² = π * (15cm)² = 225π cm².

Figury z Dwoma Parametrami – Równoległobok, Romb i Trapez

Te figury wymagają nieco większej uwagi, ponieważ ich pole oblicza się za pomocą dwóch głównych parametrów: podstawy i wysokości, lub przekątnych.

Równoległobok i Romb – Podobieństwa i Różnice

Równoległobok, figura z dwoma parami równoległych boków, ma pole obliczane ze wzoru: P = a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Romb, będący szczególnym przypadkiem równoległoboku (wszystkie boki są równe), posiada alternatywny, często prostszy wzór na pole, gdy znamy długości jego przekątnych: P = (1/2) * d1 * d2, gdzie 'd1' i 'd2' to długości przekątnych. Przekątne rombu przecinają się pod kątem prostym i dzielą się na połowy.

Przykład z życia: Ułożenie kostki brukowej na chodniku w kształcie rombu lub równoległoboku wymaga obliczenia jego powierzchni, aby oszacować ilość materiału. W przypadku rombu, jeśli przekątne mają długość 6 metrów i 8 metrów, jego pole wynosi: P = (1/2) * 6m * 8m = 24 m².

Trapez – Połączenie Dwóch Podstaw

Trapez charakteryzuje się tym, że ma jedną parę boków równoległych (nazywanych podstawami). Wzór na pole trapezu to: P = (1/2) * (a + b) * h, gdzie 'a' i 'b' to długości równoległych podstaw, a 'h' to wysokość (odległość między podstawami).

Zrozumienie, które boki są podstawami, jest kluczowe. Wysokość trapezu jest zawsze prostopadła do podstaw.

Przykład z życia: Wiele terenów, np. działki budowlane, ma kształt zbliżony do trapezu. Geodeta, mierząc powierzchnię działki, wykorzystuje ten wzór. Jeśli podstawy trapezu mają 10 metrów i 15 metrów, a wysokość wynosi 8 metrów, jego pole obliczymy jako: P = (1/2) * (10m + 15m) * 8m = (1/2) * 25m * 8m = 100 m².

Wskazówki do Efektywnego Przygotowania do Sprawdzianu

Skuteczne przygotowanie do sprawdzianu z pola figur płaskich wymaga systematyczności i praktyki.

1. Opanowanie Wzorów na Pamięć i Zrozumienie Ich Logiki

Nauka wzorów to podstawa. Ale nie tylko pamięć jest ważna. Warto zrozumieć, dlaczego dany wzór działa. Na przykład, pole prostokąta to po prostu iloczyn jego boków, bo można go podzielić na jednostkowe kwadraty. Pole trójkąta to połowa pola prostokąta o tych samych podstawach i wysokościach.

2. Rozwiązywanie Różnorodnych Zadań

Sprawdziany często zawierają zadania o zróżnicowanym stopniu trudności. Nie ograniczaj się do prostych przykładów. Pracuj nad zadaniami, w których figury są złożone, składają się z kilku mniejszych figur, lub gdzie dane są informacje pośrednie.

Przykładowe zadanie złożone: Oblicz pole figury złożonej z prostokąta o bokach 5 cm i 10 cm oraz doczepionego do jednego z dłuższych boków półkola o promieniu 5 cm. Aby rozwiązać to zadanie, należy obliczyć pole prostokąta (P_prost = 5 * 10 = 50 cm²) i pole półkola (P_półkola = (1/2) * π * 5² = 12.5π cm²). Suma tych pól to całkowite pole figury.

3. Analiza Rysunków i Schematów

Wiele zadań zawiera rysunki. Uważnie analizuj każdy element rysunku, identyfikuj znane figury i dane. Zwracaj uwagę na oznaczenia, takie jak kąty proste czy równoległe boki. Czasem trzeba dorysować linie pomocnicze, aby wyznaczyć wysokość lub inne potrzebne wymiary.

4. Praca z Jednostkami Miary

Zawsze zwracaj uwagę na jednostki miary. Pole zawsze podajemy w jednostkach kwadratowych (cm², m², km²). Upewnij się, że wszystkie wymiary w zadaniu są podane w tej samej jednostce, zanim przystąpisz do obliczeń. Konwersja jednostek jest częstym błędem.

5. Powtórka i Konsultacje

Systematycznie powtarzaj materiał. Jeśli napotkasz trudności, nie wahaj się prosić o pomoc nauczyciela lub kolegów. Warto też rozwiązywać przykładowe sprawdziany z poprzednich lat, aby zapoznać się z formatem pytań i typowymi trudnościami.

Podsumowanie

Sprawdzian z pola figur płaskich jest ważnym sprawdzianem umiejętności matematycznych na poziomie gimnazjum. Poprawne obliczanie pól wymaga nie tylko znajomości podstawowych wzorów, ale także umiejętności logicznego myślenia, analizy geometrycznej i dokładności.

Figury takie jak kwadrat, prostokąt, trójkąt, koło, równoległobok, romb i trapez, choć różnorodne, posiadają określone właściwości, które determinują sposoby obliczania ich pól. Kluczem do sukcesu jest zrozumienie tych właściwości i konsekwentne stosowanie odpowiednich wzorów.

Pamiętaj, że matematyka to nie tylko teoria. Wiele codziennych sytuacji wymaga stosowania wiedzy o figurach płaskich. Od budownictwa, przez projektowanie, aż po codzienne czynności, umiejętność ta jest niezwykle praktyczna.

Zachęcamy wszystkich uczniów do solidnego przygotowania się do sprawdzianu. Poświęćcie czas na powtórkę, ćwiczcie rozwiązywanie zadań i nie bójcie się zadawać pytań. Dobrze opanowana wiedza z zakresu pola figur płaskich będzie solidnym fundamentem do dalszej nauki matematyki i otworzy przed Wami wiele drzwi w przyszłości. Powodzenia!