Ostrosłupy Sprawdzian Z Matematyki Gim 3

Ach, sprawdzian z ostrosłupów… dla wielu uczniów klasy trzeciej gimnazjum, a także dla wspierających ich rodziców i nauczycieli, te słowa mogą wywoływać lekkie westchnienie niepewności. To temat, który potrafi sprawić, że geometria przestrzenna wydaje się nagle bardziej złożona, niżbyśmy tego chcieli. Pamiętam rozmowy z nauczycielami, którzy widzą, jak ich uczniowie zmagają się z wizualizacją brył, jak trudne bywa zrozumienie zależności między krawędzią podstawy, wysokością ostrosłupa a jego wysokością ściany bocznej. Ale spokojnie! Zrozumienie ostrosłupów jest w zasięgu ręki, a ten artykuł ma na celu rozwiać wszelkie wątpliwości i pomóc Wam przygotować się do sprawdzianu z matematyki.

Nie jesteście sami w tej matematycznej podróży. Badania PISA regularnie pokazują, że obszary związane z geometrią przestrzenną stanowią wyzwanie dla wielu uczniów na całym świecie. Ale to nie powód do zniechęcenia, lecz motywacja do lepszego zrozumienia i skuteczniejszego podejścia do nauki. Pomożemy Wam spojrzeć na ostrosłupy z innej perspektywy – bardziej praktycznej i mniej stresującej.

Dlaczego Ostrosłupy Stanowią Wyzwanie?

Zanim przejdziemy do konkretnych strategii, warto zastanowić się, skąd bierze się trudność. Głównym problemem jest zazwyczaj brak przestrzennej wyobraźni. W przeciwieństwie do figur płaskich, które możemy narysować i łatwo opisać, ostrosłupy to bryły. Wizualizacja ich kształtów, zrozumienie, jak poszczególne elementy (wierzchołki, krawędzie, ściany, wysokość) się ze sobą łączą, wymaga pewnego wysiłku.

Dodatkowo, wzory na pola powierzchni i objętości ostrosłupów, choć matematycznie logiczne, mogą wydawać się abstrakcyjne. Szczególnie trudność sprawiają różne rodzaje ostrosłupów: ostrosłupy prawidłowe (gdzie podstawa jest wielokątem foremnym, a wierzchołek leży nad środkiem podstawy) i ostrosłupy zwykłe, gdzie sytuacja jest mniej symetryczna.

Praktyczny przykład z życia: Pomyślcie o piramidach w Egipcie. To klasyczny przykład ostrosłupa. Ale czy zawsze wyobrażamy sobie dokładnie, jak te wielkie kamienne bloki łączą się, tworząc ten charakterystyczny kształt? Czy łatwo jest nam obliczyć, ile materiału potrzeba było na jej budowę (objętość) albo ile farby byśmy potrzebowali do pomalowania jej ścian bocznych (pole powierzchni)? Często nie. I właśnie dlatego potrzebujemy matematycznego podejścia.

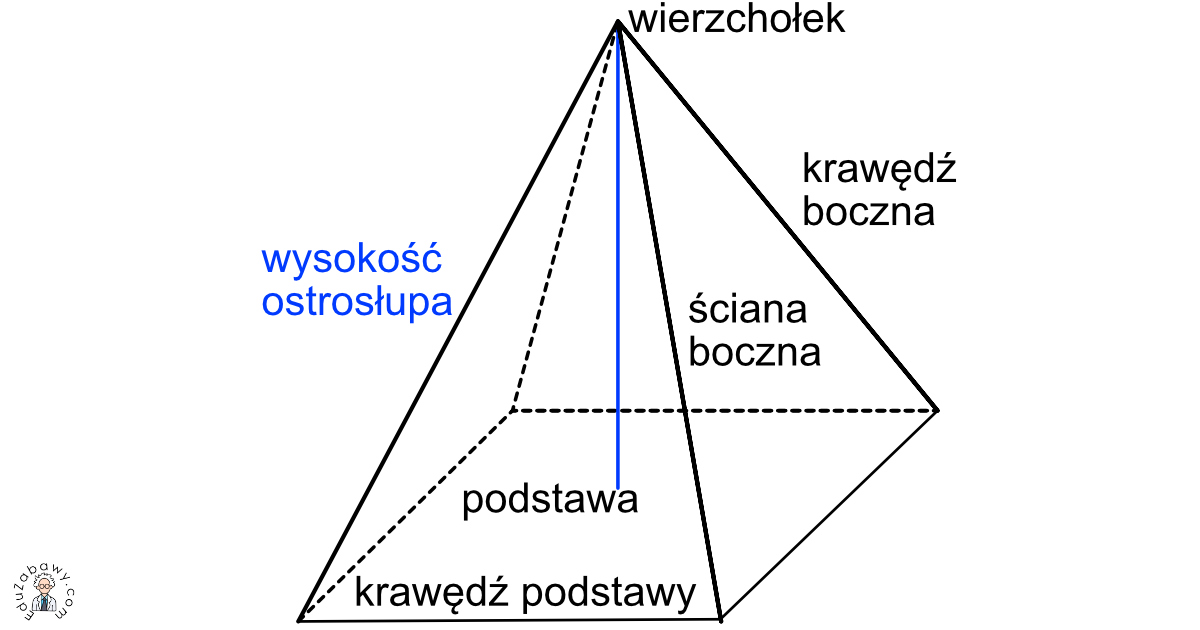
Kluczowe Elementy Ostrosłupa

Zanim weźmiemy się za rozwiązywanie zadań, upewnijmy się, że rozumiemy podstawowe pojęcia:

1. Podstawa

Podstawa ostrosłupa to wielokąt. Może to być trójkąt, czworokąt, pięciokąt… i tak dalej. Jeśli w podstawie jest trójkąt, mamy ostrosłup trójkątny. Jeśli czworokąt – ostrosłup czworokątny. Im więcej boków ma podstawa, tym „szerszy” ostrosłup.

2. Wierzchołek

To pojedynczy punkt, który nie leży w płaszczyźnie podstawy. Wszystkie krawędzie boczne zbiegają się w tym jednym punkcie.

3. Krawędzie Boczne

Są to odcinki łączące wierzchołki podstawy z wierzchołkiem ostrosłupa. W ostrosłupie o n-kątnej podstawie będzie n krawędzi bocznych.

4. Ściany Boczne

Są to trójkąty, których jednym bokiem jest bok podstawy, a dwa pozostałe to krawędzie boczne. W ostrosłupie o n-kątnej podstawie będzie n ścian bocznych.

5. Wysokość Ostrosłupa (H)

To odcinek prostopadły do płaszczyzny podstawy, poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy. To właśnie ta wysokość determinuje „ostrość” ostrosłupa.

6. Wysokość Ściany Bocznej (h_s)

W przypadku ostrosłupów prawidłowych, ściany boczne są trójkątami równoramiennymi. Wysokość ściany bocznej to wysokość jednego z tych trójkątów poprowadzona z wierzchołka ostrosłupa do podstawy ściany bocznej. Jest to niezwykle ważny wymiar przy obliczaniu pola powierzchni bocznej.

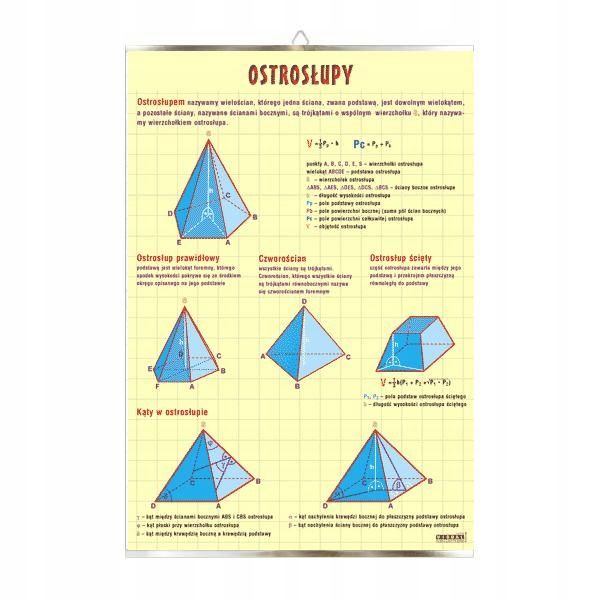
Rodzaje Ostrosłupów – Klucz do Rozwiązywania Zadań

Rozróżnienie typów ostrosłupów jest kluczowe. Na sprawdzianie pojawią się zapewne zadania dotyczące:

1. Ostrosłupy Prawidłowe

Tutaj panuje porządek! Podstawa jest wielokątem foremnym (np. kwadrat, trójkąt równoboczny, sześciokąt foremny). Dodatkowo, wierzchołek ostrosłupa znajduje się dokładnie nad środkiem geometrycznym podstawy. W rezultacie wszystkie krawędzie boczne są sobie równe, a wszystkie ściany boczne są identycznymi trójkątami równoramiennymi. To znacznie ułatwia obliczenia.

Przykład z sali lekcyjnej: Nauczyciel rysuje na tablicy ostrosłup prawidłowy czworokątny (czyli z kwadratem w podstawie). Pokazuje, że ściany boczne są takie same. Prosi uczniów o wizualizację, jak wyglądałaby siatka takiego ostrosłupa – jeden kwadrat i cztery identyczne trójkąty dookoła niego.

2. Ostrosłupy Zwykłe

Tutaj zasady są mniej restrykcyjne. Podstawa może być dowolnym wielokątem, a wierzchołek nie musi leżeć nad środkiem podstawy. W praktyce oznacza to, że krawędzie boczne i ściany boczne mogą być różne, co komplikuje obliczenia.

Pamiętajmy: Większość zadań na poziomie gimnazjum skupia się na ostrosłupach prawidłowych, ponieważ są one bardziej uporządkowane i pozwalają na wyćwiczenie podstawowych wzorów. Jednak warto wiedzieć, że ostrosłupy mogą być też bardziej złożone.

Wzory, Które Musisz Znać

Bez znajomości podstawowych wzorów, sprawdzian będzie naprawdę trudny. Oto te najważniejsze:

Pole Powierzchni Całkowitej (P_c)

Pole powierzchni całkowitej to suma pola podstawy i pól wszystkich ścian bocznych.

P_c = P_p + P_b

Gdzie:

• P_p – pole podstawy
• P_b – pole powierzchni bocznej (suma pól wszystkich ścian bocznych)

Dla ostrosłupa prawidłowego o n-kątnej podstawie, pole powierzchni bocznej można obliczyć jako:

P_b = n * (pole jednego trójkąta bocznego)

Pole trójkąta to 1/2 * podstawa * wysokość. W naszym przypadku, podstawa to bok podstawy ostrosłupa (a), a wysokość to wysokość ściany bocznej (h_s).

P_b = n * (1/2 * a * h_s)

Objętość (V)

Objętość ostrosłupa jest zawsze taka sama, niezależnie od tego, czy jest prawidłowy, czy nie.

V = 1/3 * P_p * H

Gdzie:

• P_p – pole podstawy
• H – wysokość ostrosłupa

Ważna wskazówka od nauczycieli: Często w zadaniach nie podaje się wprost wysokości ściany bocznej (h_s) ani wysokości ostrosłupa (H). Trzeba je obliczyć, korzystając z twierdzenia Pitagorasa, które łączy krawędź boczną, wysokość ostrosłupa i połowę przekątnej podstawy (w przypadku ostrosłupa prawidłowego czworokątnego) lub wysokość podstawy (w przypadku ostrosłupa prawidłowego trójkątnego).

Przykładowe zastosowanie twierdzenia Pitagorasa: W ostrosłupie prawidłowym czworokątnym z kwadratową podstawą o boku 'a' i wysokością ostrosłupa 'H', mamy trójkąt prostokątny utworzony przez:

• wysokość ostrosłupa (H)
• odcinek od środka kwadratu do środka boku kwadratu (czyli a/2)
• wysokość ściany bocznej (h_s)

Zatem: (a/2)² + H² = h_s²

Jak Przygotować Się do Sprawdzianu? Praktyczne Wskazówki

Przejdźmy do konkretów. Co możecie zrobić, aby czuć się pewniej na sprawdzianie?

1. Zrozumienie Geometrii Przestrzennej – Wizualizacja to Klucz!

Co robić:

• Rysujcie! Nie bójcie się szkicować ostrosłupów z różnych perspektyw. Narysujcie podstawę, a potem zaznaczcie wierzchołek i połączcie go z wierzchołkami podstawy.
• Używajcie obiektów z życia codziennego: Pomyślcie o pudełku pizzy (ostrosłup czworokątny), namiocie (często ma kształt ostrosłupa), lub samych piramidach.
• Modele przestrzenne: Jeśli macie możliwość, zbudujcie prosty model ostrosłupa z kartonu lub plasteliny. To naprawdę pomaga zrozumieć jego budowę.

2. Analiza Wzorów – Nie tylko Pamięć, ale Zrozumienie

Co robić:

• Rozłóżcie wzór na czynniki: Zamiast wkuwać "P_c = P_p + P_b", zastanówcie się, co to oznacza – suma wszystkiego, co widzimy z zewnątrz.
• Ćwiczcie obliczanie P_p i P_b osobno: Zanim połączycie wszystko w całość, upewnijcie się, że potraficie obliczyć pole podstawy (zależnie od jej kształtu – kwadrat, trójkąt równoboczny itp.) oraz pole jednej ściany bocznej.
• Zwracajcie uwagę na jednostki: Czy wszystkie dane są w centymetrach? Czy wynik ma być w cm² czy cm³?

3. Rozwiązywanie Zadań – Klucz do Sukcesu

Co robić:

• Zacznijcie od prostych zadań: Najpierw te, gdzie wszystkie wymiary są podane bezpośrednio.
• Stopniowo zwiększajcie trudność: Przechodźcie do zadań, gdzie trzeba obliczyć brakujące wymiary za pomocą twierdzenia Pitagorasa.
• Analizujcie przykładowe zadania: Przejrzyjcie zadania z podręcznika lub poprzednich sprawdzianów z rozwiązaniami. Zrozumcie, krok po kroku, jak dojść do wyniku.
• Nie bójcie się pytać! Jeśli czegoś nie rozumiecie, zapytajcie nauczyciela, kolegę lub rodzica. Lepiej wyjaśnić wątpliwości teraz, niż stresować się na sprawdzianie.

4. Rola Rodziców i Nauczycieli – Wspólna Nauka

Dla rodziców:

• Wsparcie, nie nacisk: Pomóżcie stworzyć spokojną atmosferę do nauki. Niekoniecznie musicie być ekspertami od matematyki, ale możecie być dobrym słuchaczem i motywatorem.
• Wspólne rozwiązywanie problemów: Czasem wspólne spojrzenie na zadanie z innej perspektywy może pomóc.
• Gry i zabawy: Poszukajcie w Internecie gier edukacyjnych związanych z geometrią przestrzenną.

Dla nauczycieli:

• Używajcie pomocy dydaktycznych: Modele brył, wizualizacje 3D na tablicy interaktywnej mogą znacząco ułatwić zrozumienie.
• Dostosujcie tempo: Pamiętajcie o zróżnicowaniu potrzeb uczniów.
• Pozytywne wzmocnienie: Chwalcie za wysiłek i postępy, nie tylko za poprawne wyniki.

Podsumowanie

Sprawdzian z ostrosłupów może wydawać się trudny, ale z właściwym podejściem, systematyczną pracą i wsparciem jest jak najbardziej do pokonania. Pamiętajcie o wizualizacji, zrozumieniu wzorów, a przede wszystkim – o ćwiczeniu. Każde rozwiązane zadanie to krok bliżej do sukcesu. Nie poddawajcie się, a efekty na pewno się pojawią! Powodzenia na sprawdzianie!