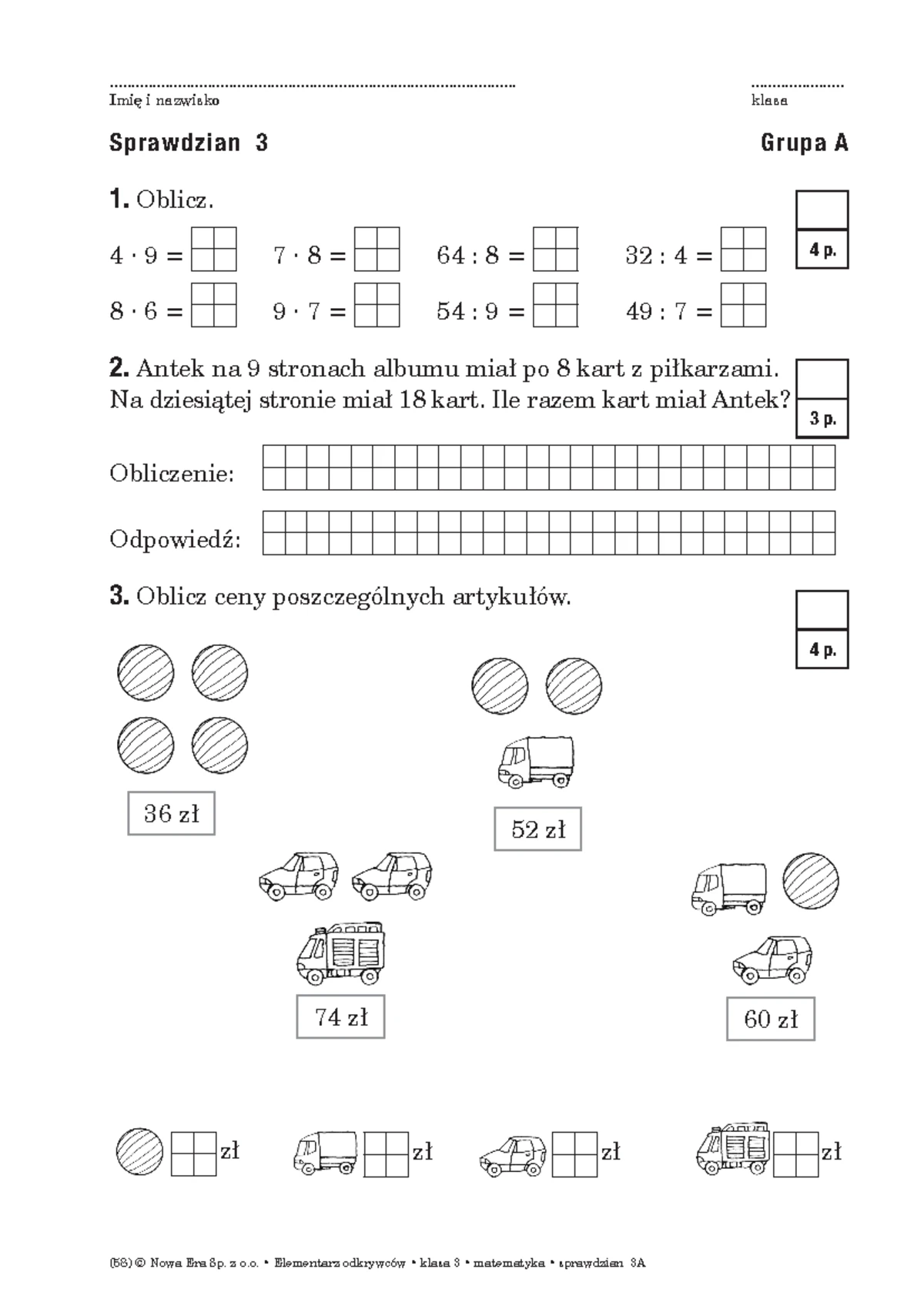
Matematyka Sprawdzian Klasa 6 Dział 3 Gwo

Słońce delikatnie przebijało się przez firanki, budząc Julkę do nowego dnia. Dziś był ten dzień. Dzień, na który czekała z lekkim niepokojem, ale i z odrobiną ekscytacji. Wczoraj wieczorem, siedząc przy kuchennym stole, próbowała rozwiązać ostatnie zadanie z Działu 3 GWO, które dotyczyło obliczania pól figur. Mama, widząc jej skupioną minę, uśmiechnęła się ciepło. "Pamiętaj, Julka," powiedziała, "każdy trudny problem można rozłożyć na mniejsze części. Tak jakbyśmy dzielili dużą pizzę na kawałki. Każdy kawałek jest łatwiejszy do zjedzenia." Julka przytaknęła, biorąc do ręki swój ołówek i patrząc na skomplikowany wzór. Ta prosta metafora, jak wiele innych, które jej rodzice często jej powtarzali, pomogła jej podejść do zadania z nową energią. Po kilku minutach intensywnego myślenia, nagle wszystko stało się jasne. Rozwiązanie, które wcześniej wydawało się nieosiągalne, teraz ukazało się przed nią w całej swojej prostocie.
Ten poranek zwiastował kolejny etap tej matematycznej podróży – Sprawdzian Klasa 6 Dział 3 GWO. Matematyka, dla wielu uczniów, bywa jak ta skomplikowana mapa, której trzeba nauczyć się odczytywać, by dotrzeć do celu. Niektóre zadania przypominają labirynty, inne wyzwania, które wymagają logicznego myślenia i spostrzegawczości. Ale podobnie jak Julka, każdy z nas ma w sobie narzędzia, by te matematyczne wyzwania pokonać. Kluczem, jak się okazuje, jest nie tylko zapamiętywanie wzorów, ale przede wszystkim zrozumienie, co one oznaczają i jak je zastosować w praktyce.
Wróćmy do tej "pizzy", którą mama Julki tak trafnie przywołała. W Dział 3 podręcznika GWO, uczniowie klasy szóstej mierzą się z zagadnieniami, które często sprowadzają się właśnie do takiego "dzielenia problemu na części". Kiedy na sprawdzianie pojawi się zadanie wymagające obliczenia pola trapezu, a wcześniej ćwiczyliśmy pola prostokąta i pola trójkąta, możemy wykorzystać tę wiedzę. Trapez możemy przecież wyobrazić sobie jako dwa trójkąty i prostokąt, a wtedy jego pole staje się sumą prostszych pól. To jest właśnie ta siła matematyki – budowanie jednej umiejętności na drugiej, tworząc solidne fundamenty dla coraz trudniejszych zagadnień.
Kiedy patrzymy na karty pracy z Działu 3 GWO, widzimy tam wiele nowych pojęć, takich jak obwód wielokąta, czy też bardziej złożone figury jak romb czy równoległobok. Na pierwszy rzut oka mogą wydawać się one przytłaczające. Ale jeśli zastosujemy zasadę Julki – dzielenia na części – stają się one o wiele bardziej przystępne. Na przykład, aby obliczyć pole równoległoboku, musimy zrozumieć jego związek z prostokątem. Zawsze możemy "wyciąć" fragment i "przenieść" go, tworząc prostokąt o tym samym polu. Ta wizualizacja, to "widzenie" figury w inny sposób, jest często kluczem do sukcesu. To jak składanie puzzli – każdy element ma swoje miejsce i pasuje do innych.
Warto też pamiętać o codziennych zastosowaniach matematyki, które często pomagają nam zrozumieć abstrakcyjne wzory. Kiedy planujemy remont pokoju i musimy obliczyć, ile farby potrzebujemy na pomalowanie ścian, albo ile płytek kupić na podłogę, tak naprawdę stosujemy te same zasady, które poznajemy na lekcjach. Obliczanie pól powierzchni ścian to dokładnie to samo, co obliczanie pola prostokąta czy innych figur. A kiedy trzeba zaplanować układ mebli, mierząc przestrzeń, również pracujemy z wymiarami i kształtami. Te praktyczne przykłady sprawiają, że matematyka przestaje być tylko zbiorem abstrakcyjnych reguł, a staje się użytecznym narzędziem w naszym życiu.
Ważne jest, aby podczas przygotowań do sprawdzianu z Klasy 6, Dział 3 GWO, nie tylko rozwiązywać zadania, ale też zastanawiać się, dlaczego dane wzory działają. Zrozumienie logiki stojącej za matematycznymi formułami jest o wiele cenniejsze niż mechaniczne zapamiętywanie. Kiedy wiemy, skąd wziął się wzór na pole trójkąta (jego związek z polem prostokąta), łatwiej nam go zapamiętać i zastosować. To podobne do nauki języka obcego – jeśli znamy gramatykę i potrafimy tworzyć zdania, a nie tylko zapamiętywać pojedyncze słowa, o wiele łatwiej nam się komunikować.
Nauczyciele często powtarzają, że matematyka uczy nas myślenia. I to jest prawda. Wymaga precyzji, analizy, a także umiejętności dostrzegania związków między różnymi elementami. Kiedy rozwiązujemy zadania z Działu 3 GWO, rozwijamy te umiejętności. Uczymy się, jak podejść do problemu, jak szukać rozwiązania, a także jak sprawdzić, czy nasze rozwiązanie jest poprawne. To są umiejętności, które przydadzą się nam nie tylko w szkole, ale w całym życiu. W każdej sytuacji, gdy będziemy musieli podjąć jakąś decyzję, analizować dostępne informacje, czy rozwiązywać napotkane trudności.
Nawet jeśli w dniu sprawdzianu poczujemy się niepewnie, warto przypomnieć sobie historię Julki i "podzielić problem na części". Każde zadanie, nawet to najtrudniejsze, można rozłożyć na mniejsze, łatwiejsze do strawienia etapy. Zastosowanie zdobytej wiedzy, wizualizacja problemu, a nawet odniesienie do codziennych sytuacji – to wszystko może pomóc. Matematyka w Klasie 6, Dział 3 GWO, to nie tylko cyfry i wzory, to także nauka logicznego myślenia, systematyczności i wiary we własne siły.
Na koniec dnia, kiedy sprawdzian będzie już za nami, niezależnie od wyniku, ważne jest, aby wyciągnąć z tej lekcji cenną lekcję. Nie chodzi tylko o ocenę, ale o proces uczenia się. O pokonywanie własnych słabości, o rozwijanie cierpliwości i wytrwałości. Każdy sprawdzian to kolejny krok na naszej edukacyjnej ścieżce. To szansa, by dowiedzieć się czegoś nowego o sobie i o świecie. A matematyka, jak pokazuje Dział 3, jest fascynującą częścią tego świata, która czeka, by ją odkryć.