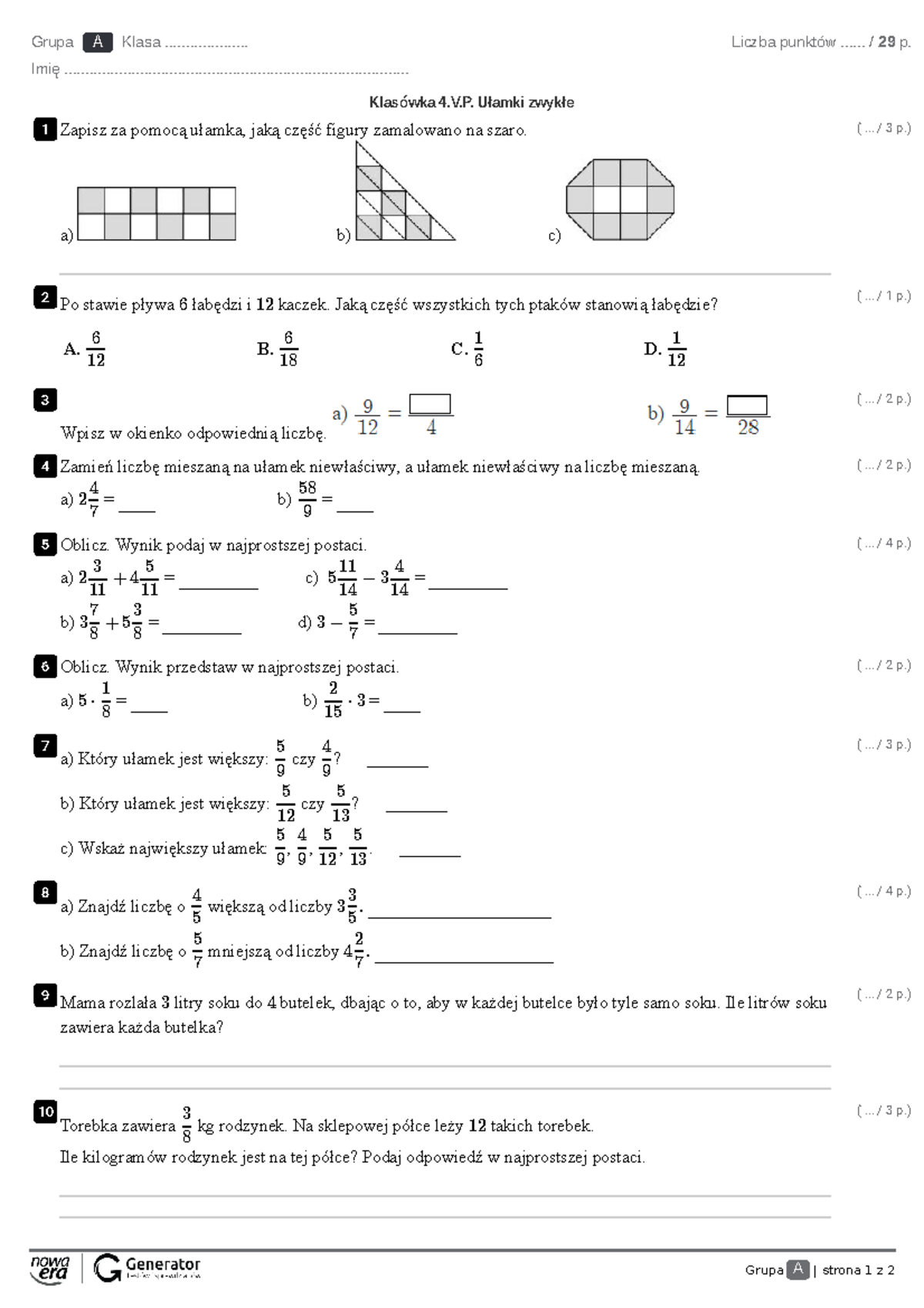
Matematyka Kl 5 Ułamki Zwykłe Sprawdzian

Ułamki zwykłe stanowią fundamentalny element edukacji matematycznej, wprowadzany w klasie piątej szkoły podstawowej. Są to liczby reprezentujące część całości, zapisane jako stosunek dwóch liczb naturalnych: licznika (liczba na górze) i mianownika (liczba na dole), oddzielonych kreską ułamkową. Zrozumienie tego konceptu jest kluczowe dla dalszego rozwoju matematycznego, ponieważ stanowi bazę do nauki bardziej zaawansowanych zagadnień, takich jak liczby dziesiętne, procenty, a nawet algebra. Sprawdzian z ułamków zwykłych w klasie piątej ma na celu ocenę stopnia opanowania tych podstawowych umiejętności.

Czym są ułamki zwykłe i dlaczego są ważne?

Ułamek zwykły, zapisywany w postaci ^a⁄_b, gdzie a to licznik, a b to mianownik (b ≠ 0), określa, ile części z całości bierzemy. Na przykład, ułamek ¹⁄₂ oznacza jedną z dwóch równych części. W klasie piątej uczniowie poznają podstawowe operacje na ułamkach: porównywanie, dodawanie, odejmowanie, mnożenie i dzielenie, a także skracanie i rozszerzanie ułamków. Opanowanie tych umiejętności nie jest jedynie celem samym w sobie; stanowi ono pomost do bardziej złożonych koncepcji matematycznych.

Dlaczego ułamki są tak istotne? Profesor Joanna K., specjalistka ds. dydaktyki matematyki, podkreśla: "Ułamki wprowadzają uczniów w świat liczb niecałkowitych, rozwijając ich intuicję liczbową i zdolność do myślenia abstrakcyjnego. Bez solidnych podstaw w zakresie ułamków, uczniowie napotykają trudności w dalszej nauce, co może prowadzić do zniechęcenia i obniżenia wyników w przedmiotach ścisłych."

Sprawdzian z ułamków zwykłych w klasie piątej służy jako narzędzie diagnostyczne. Pozwala nauczycielowi ocenić, czy uczniowie zrozumieli definicję ułamka, potrafią przedstawić go graficznie, a przede wszystkim, czy są w stanie wykonywać podstawowe działania matematyczne z ich udziałem. Wyniki sprawdzianu informują nie tylko o indywidualnych postępach ucznia, ale także o efektywności metod nauczania stosowanych przez nauczyciela.

Jak ułamki wpływają na rozwój ucznia?

Nauka ułamków zwykłych ma znaczący wpływ na rozwój poznawczy uczniów. Proces ten wymaga od nich:

Abstrakcyjnego myślenia: Ułamki reprezentują koncepty, które nie mają bezpośredniego odpowiednika w świecie konkretnych przedmiotów, co stymuluje rozwój zdolności do operowania symbolami i abstrakcyjnymi ideami.
Precyzyjnego formułowania myśli: Poprawne używanie terminologii matematycznej (licznik, mianownik, kreska ułamkowa) oraz umiejętność logicznego wyjaśniania kroków przy rozwiązywaniu zadań rozwijają zdolności komunikacyjne.
Rozwiązywania problemów: Zadania matematyczne wymagają analizy, planowania i stosowania odpowiednich strategii. Ułamki często pojawiają się w zadaniach problemowych, ucząc uczniów systematycznego podejścia.
Wytrwałości i cierpliwości: Opanowanie ułamków, szczególnie trudniejszych operacji, może wymagać wielokrotnych prób i błędów, co kształtuje postawę determinacji i niepoddawania się.

Z drugiej strony, trudności z ułamkami mogą generować negatywne emocje. Uczeń, który nie radzi sobie z tym materiałem, może odczuwać frustrację, strach przed matematyką, a nawet obniżenie poczucia własnej wartości. Psycholog szkolny Anna M. zauważa: "Systematyczne porażki w opanowaniu kluczowych zagadnień, takich jak ułamki, mogą prowadzić do powstania tzw. 'lęku matematycznego'. Ważne jest, aby wcześnie identyfikować te trudności i oferować wsparcie, zarówno w postaci dodatkowych ćwiczeń, jak i wsparcia psychologicznego."

Badania i ekspertyzy

Międzynarodowe badania, takie jak PISA, wielokrotnie wskazywały na znaczenie umiejętności matematycznych, w tym operowania ułamkami, dla ogólnych wyników uczniów w nauce i ich przyszłych szans edukacyjnych i zawodowych. Raport OECD z jednego z takich badań stwierdza: "Podstawowe kompetencje matematyczne, takie jak rozumienie i stosowanie ułamków, są predyktorem sukcesu w wielu dziedzinach życia, od zarządzania finansami osobistymi po podejmowanie złożonych decyzji zawodowych."

Polscy nauczyciele matematyki również podkreślają rolę sprawdzianów z ułamków. Pan Jan K., doświadczony polonista, mówi: "Sprawdzian to nie tylko ocena, ale przede wszystkim informacja zwrotna. Dzięki niemu wiem, które zagadnienia wymagają powtórzenia, a które uczniowie już opanowali. To pozwala mi na indywidualizację nauczania i dostosowanie tempa pracy do potrzeb klasy."

Praktyczne zastosowania ułamków w życiu ucznia

Choć na pierwszy rzut oka ułamki mogą wydawać się abstrakcyjnym pojęciem szkolnym, ich zastosowanie w życiu codziennym jest wszechobecne. Uczniowie klasy piątej mogą dostrzec ich użyteczność w:

Gotowaniu i pieczeniu: Przepisy często podają składniki w ułamkach (np. ¹⁄₂ szklanki mąki, ¹⁄₄ łyżeczki soli). Aby przygotować potrawę, trzeba umieć odmierzyć te ilości, a także czasem przeliczyć proporcje, gdy chcemy przygotować mniejszą lub większą porcję.
Podziale dóbr: Dzielenie się pizzą, ciastem, czekoladą z rodzeństwem lub przyjaciółmi naturalnie wiąże się z koncepcją ułamków. Jeśli dzielimy pizzę na 8 kawałków i każdy zje ¹⁄₈, to zrozumienie tego prostego podziału jest już ćwiczeniem z ułamków.
Zakupach: Promocje typu "¹⁄₃ taniej" czy "kup 2, trzeci za ¹⁄₂ ceny" wymagają od ucznia umiejętności porównywania ułamków i szacowania wartości obniżki.
Pomiarach: Przy drobnych pracach rękodzielniczych, majsterkowaniu, a nawet czytaniu instrukcji montażu mebli, mogą pojawić się jednostki miary zapisane ułamkami (np. ³⁄₈ cala).
Zegar i czas: Połowa godziny (¹⁄₂), kwadrans (¹⁄₄) to intuicyjne rozumienie ułamków czasu, które uczniowie wykorzystują na co dzień.

Sprawdzian z ułamków zwykłych w klasie piątej jest zatem ważnym etapem edukacyjnym. Stanowi on zarówno test wiedzy, jak i okazję do utrwalenia umiejętności, które mają realne zastosowanie w życiu. Sukces w tym sprawdzianie buduje pewność siebie ucznia i przygotowuje go do dalszych wyzwań matematycznych, jednocześnie potwierdzając, że matematyka jest narzędziem użytecznym w wielu aspektach codzienności.