Gwo Sprawdzian Matematyka 1 Gimnazjum Symetrie

Drodzy Uczniowie i Szanowni Rodzice,

Wiemy, że nadchodzący sprawdzian z matematyki, szczególnie ten dotyczący symetrii, może budzić pewne obawy. To zupełnie naturalne! Czasem nowe pojęcia, nawet te wizualnie intuicyjne, mogą wydawać się na pierwszy rzut oka skomplikowane. Chcemy jednak Was zapewnić, że temat symetrii wcale nie jest taki straszny, a wręcz przeciwnie – jest fascynujący i obecny wszędzie dookoła nas. Ten artykuł ma na celu nie tylko przygotować Was do sprawdzianu, ale przede wszystkim pokazać piękno i praktyczne zastosowania symetrii, rozjaśnić wszelkie wątpliwości i sprawić, że matematyka stanie się dla Was bardziej przyjazna.

Zrozumieć Symetrię – To Prostsze Niż Myślisz!

Co właściwie kryje się pod pojęciem symetrii? Najprościej mówiąc, to pewien rodzaj harmonii i równowagi. Gdy coś jest symetryczne, oznacza to, że można znaleźć linię lub punkt, względem którego obie jego strony są swoimi lustrzanymi odbiciami. Wyobraźcie sobie, że kładziecie coś na lustrze – jeśli odbicie jest identyczne z drugą połową obiektu, to mamy do czynienia z symetrią.

Nauczyciele często podkreślają, że symetria to jeden z fundamentalnych elementów matematyki, który pomaga nam opisywać i rozumieć świat. Niektórzy badacze, jak matematyk Hermann Weyl, pisali o symetrii jako o "nieświadomej potrzebie człowieka". To pokazuje, jak głęboko zakorzenione jest to pojęcie w naszej psychice i jak bardzo go szukamy w otaczającej nas rzeczywistości.

Rodzaje Symetrii, Które Poznacie

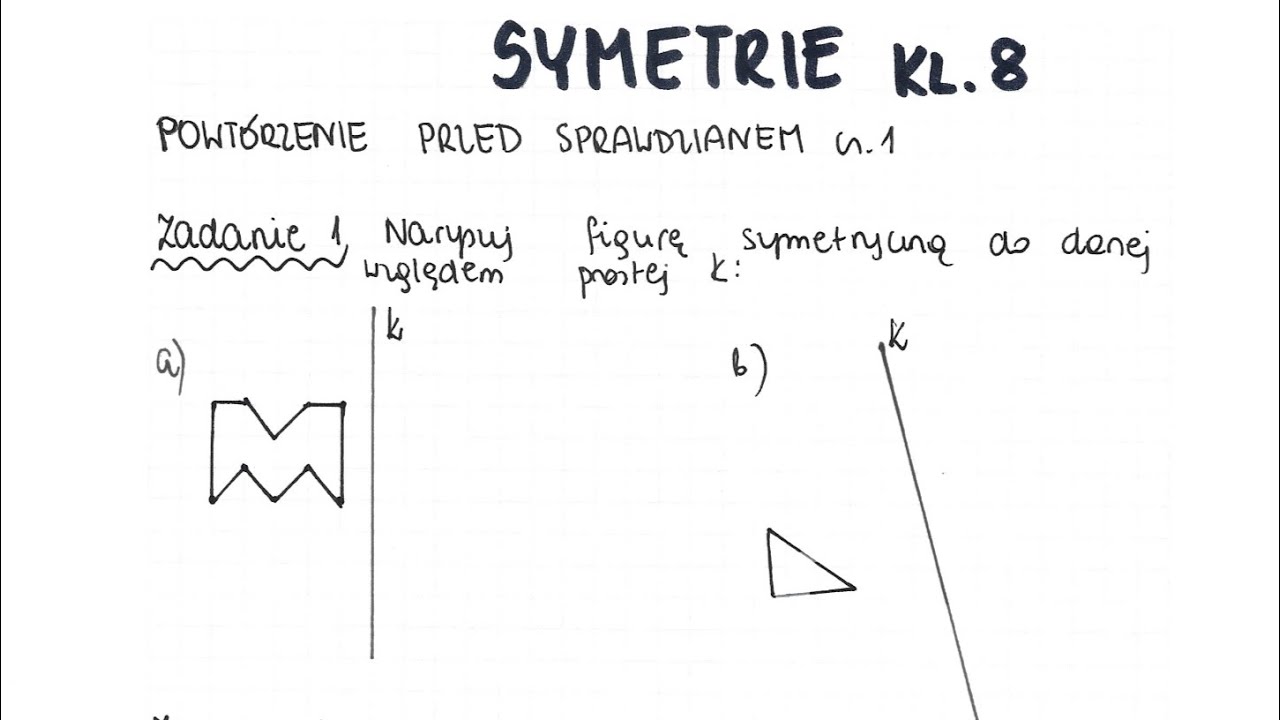
Na poziomie pierwszej klasy gimnazjum skupicie się głównie na dwóch rodzajach symetrii:

1. Symetria osiowa (zwierciadlana): To ta, o której myślimy najczęściej, gdy mówimy o lustrzanym odbiciu. Jest ona określona przez oś symetrii – prostą. Każdy punkt po jednej stronie osi ma swój odpowiednik po drugiej stronie, w tej samej odległości od osi i po jej "przeciwnej stronie".
2. Symetria środkowa: Tutaj mamy do czynienia z punktem symetrii. Obiekt jest symetryczny względem tego punktu, jeśli dla każdego jego punktu istnieje punkt po przeciwnej stronie punktu symetrii, w tej samej odległości od niego. Wyobraźcie sobie obrót o 180 stopni wokół tego punktu – obraz powinien pozostać taki sam.

Zrozumienie tych dwóch typów to klucz do sukcesu na sprawdzianie. Pamiętajcie, że ćwiczenie czyni mistrza, a im więcej będziecie pracować z tymi pojęciami, tym bardziej będą one dla Was oczywiste.

Gdzie Spotykamy Symetrię na Co Dzień?

Często słyszymy od uczniów: "Po co mi ta matematyka? Gdzie to się przyda?". Odpowiedź jest prosta: wszędzie! Symetria jest wszechobecna:

• W Naturze: Popatrzcie na motyle – ich skrzydła są niemal idealnie symetryczne osiowo. Liście drzew, płatki kwiatów, a nawet budowa wielu zwierząt (jak ludzka twarz czy ciało) wykazują symetrię. To zasługa ewolucji, która często faworyzuje formy proste i efektywne.
• W Sztuce i Architekturze: Od starożytnych świątyń po nowoczesne budynki, symetria jest kluczowym narzędziem w tworzeniu harmonijnych i estetycznych kompozycji. Kościoły, katedry, pałace – wiele z nich opiera swoją strukturę na zasadach symetrii osiowej.
• W Przedmiotach Codziennego Użytku: Krzesło, stół, większość naczyń, a nawet ubrania – wiele z nich jest symetrycznych, co ułatwia ich produkcję i użytkowanie.
• W Designie i Grafice: Logo firm, plakaty, strony internetowe – projektanci świadomie wykorzystują symetrię, aby przyciągnąć uwagę, nadać przekazowi czytelność i stworzyć przyjemny dla oka wygląd.

Jak widać, symetria to nie tylko abstrakcyjne pojęcie matematyczne, ale narzędzie, które kształtuje nasz świat. Zrozumienie jej zasad pozwala lepiej docenić otaczające nas piękno.

Jak Nauczyciele Podchodzą do Nauczania Symetrii?

Wielu pedagogów, jak wskazują badania i obserwacje, kładzie nacisk na wizualne i praktyczne aspekty nauczania symetrii. "Chcemy, aby uczniowie czuli symetrię, a nie tylko ją liczyli" – mówi Pani Anna Kowalska, doświadczona nauczycielka matematyki. "Dlatego często używamy przykładów z życia, rysujemy, wycinamy, bawimy się lustrem. Kiedy dzieci zobaczą symetrię w motylu czy w swoim odbiciu, łatwiej im zrozumieć abstrakcyjną definicję."

Kluczem jest łączenie teorii z praktyką. Matematyka nie powinna być tylko zbiorem suchych wzorów, ale narzędziem do odkrywania świata. Dlatego przygotowaliśmy dla Was kilka praktycznych wskazówek i ćwiczeń.

Przygotowanie do Sprawdzianu – Krok po Kroku

Nie martwcie się! Dobra organizacja i systematyczne podejście to klucz do sukcesu.

1. Zrozumienie Podstawowych Definicji

Symetria osiowa:

• Potrzebna jest oś symetrii (linia).
• Figury symetryczne są jak odbicia lustrzane.
• Odległość punktu od osi jest taka sama po obu stronach.

Symetria środkowa:

• Potrzebny jest punkt symetrii.
• Figury symetryczne są jak po obrocie o 180 stopni.
• Odległość punktu od środka jest taka sama po obu stronach.

2. Ćwiczenia z Rysowania i Konstruowania

Weźcie kartkę papieru, linijkę i ołówek.

• Symetria osiowa: Narysujcie prostą linię (oś). Narysujcie dowolny punkt. Użyjcie linijki, aby zaznaczyć punkt symetryczny po drugiej stronie, w tej samej odległości od osi. Powtórzcie to dla kilku punktów, aby narysować symetryczny odcinek, potem trójkąt, kwadrat. Możecie też spróbować naszkicować połowę motyla i dorysować drugą symetryczną połowę.
• Symetria środkowa: Narysujcie punkt (środek symetrii). Narysujcie dowolny punkt. Połączcie go z punktem środkowym linią. Zaznaczcie punkt po drugiej stronie, w tej samej odległości od środka (możecie użyć cyrkla lub linijki). Powtórzcie dla kilku punktów, aby narysować symetryczny odcinek, potem równoległobok.

Wskazówka od ekspertów: "Najlepsze efekty daje łączenie teorii z praktycznym działaniem. Kiedy uczniowie sami tworzą figury symetryczne, widzą, jak działa symetria i zapamiętują zasady na dłużej" – sugeruje metodyk nauczania matematyki, Pan Janusz Nowak.

3. Zadania z Lustrem

To fantastyczne i proste ćwiczenie!

• Połóżcie małe lusterko na osi symetrii, którą narysowaliście na kartce. Zobaczcie, jak odbicie uzupełnia figurę.
• Spróbujcie odtworzyć rysunek, widząc tylko jego połowę w lustrze.
• Szukajcie przedmiotów w domu, które wykazują symetrię osiową lub środkową.

4. Rozpoznawanie Symetrii na Obrazkach

Znajdźcie w internecie lub w książkach przykłady różnych obiektów (zwierzęta, rośliny, budowle, wzory). Waszym zadaniem jest zidentyfikowanie osi lub punktu symetrii i określenie, czy obiekt jest symetryczny. To ćwiczy Waszą spostrzegawczość i umiejętność analizy.

5. Rozwiązywanie Zadań z Podręcznika i Zeszytu Ćwiczeń

Podręcznik i zeszyt ćwiczeń zawierają mnóstwo zadań przygotowanych specjalnie na ten temat. Systematyczne ich rozwiązywanie pozwoli Wam utrwalić wiedzę i zobaczyć, jakiego typu pytania mogą pojawić się na sprawdzianie. Nie bójcie się ich, traktujcie jako wyzwanie i okazję do nauki.

Pokonaj Strach Przed Sprawdzianem!

Strach przed sprawdzianem często wynika z niepewności. Kiedy lepiej zrozumiemy materiał, nasza pewność siebie rośnie. Pamiętajcie:

• Nie jesteście sami. Wasz nauczyciel jest po to, aby Wam pomóc. Jeśli czegoś nie rozumiecie, pytajcie! Lepiej zadać pytanie na lekcji niż męczyć się w domu.
• Małe kroki. Nie próbujcie nauczyć się wszystkiego na raz. Podzielcie materiał na mniejsze części i pracujcie systematycznie.
• Pozytywne nastawienie. Wiara w swoje możliwości jest bardzo ważna. Zamiast myśleć "nie dam rady", powiedzcie sobie "nauczę się tego".
• Sen i odpoczynek. Przed sprawdzianem ważne jest, aby dobrze się wyspać. Zmęczony umysł gorzej funkcjonuje.

Symetria to piękny i logiczny dział matematyki. Kiedy ją zrozumiecie, zobaczycie, jak wiele się dzięki niej wyjaśnia w świecie, który nas otacza. Niech ten sprawdzian będzie dla Was okazją do pokazania, jak wiele potraficie! Pracujcie sumiennie, a efekty na pewno się pojawią.

Trzymamy za Was mocno kciuki!