Funkcje Wymierne Sprawdzian Matematyka 2

Czy funkcja wymierna spędza Ci sen z powiek przed zbliżającym się sprawdzianem? Nie jesteś sam! Wiele osób uważa ten temat za jeden z trudniejszych w kursie matematyki na poziomie klasy drugiej liceum lub technikum. Jednak z odpowiednim podejściem i zrozumieniem kluczowych zagadnień, nawet najbardziej zawiłe funkcje wymierne mogą stać się prostsze do opanowania. W tym artykule przeprowadzimy Cię krok po kroku przez najważniejsze aspekty funkcji wymiernych, abyś mógł poczuć się pewniej na sprawdzianie.

Funkcje Wymierne: Podstawy i Kluczowe Pojęcia

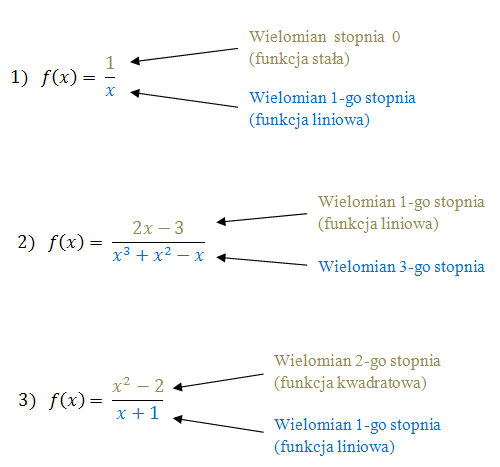
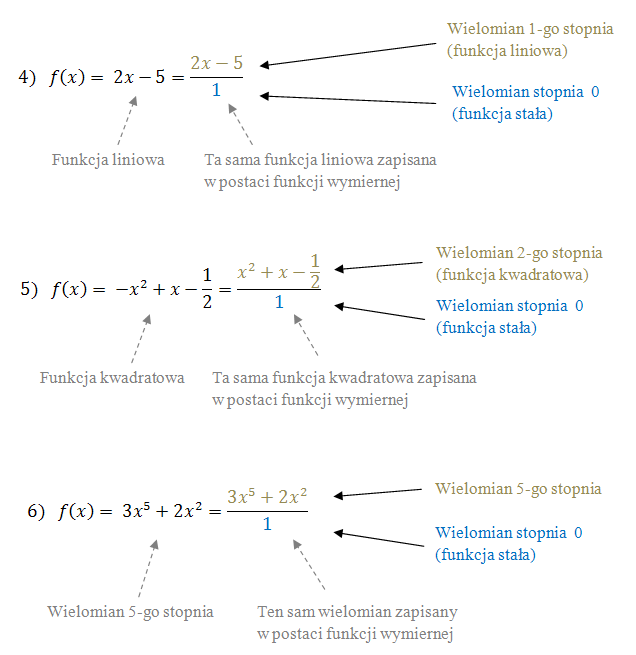
Zacznijmy od definicji. Czym właściwie jest funkcja wymierna? Najprościej mówiąc, jest to funkcja, którą można zapisać jako iloraz dwóch wielomianów. Formalnie, funkcja $f(x) = \frac{P(x)}{Q(x)}$ jest wymierna, gdzie $P(x)$ i $Q(x)$ są wielomianami, a $Q(x)$ jest wielomianem niezerowym. To ostatnie jest kluczowe – mianownik nigdy nie może być równy zero, ponieważ dzielenie przez zero jest matematycznie niedozwolone.

Dziedzina Funkcji Wymiernej

Pierwszym i absolutnie fundamentalnym krokiem przy analizie każdej funkcji wymiernej jest określenie jej dziedziny. Dziedzina to zbiór wszystkich argumentów $x$, dla których funkcja jest określona. W przypadku funkcji wymiernych, musimy wykluczyć te wartości $x$, które powodują, że mianownik staje się równy zero. Aby to zrobić, rozwiązujemy równanie $Q(x) = 0$. Rozwiązania tego równania to właśnie te wartości, które należy wykluczyć z dziedziny funkcji.

Przykład: Rozważmy funkcję $f(x) = \frac{x+1}{x-2}$. Aby znaleźć dziedzinę, rozwiązujemy $x-2=0$, co daje $x=2$. Zatem dziedziną funkcji jest zbiór wszystkich liczb rzeczywistych z wyjątkiem 2. Zapisujemy to jako $D = \mathbb{R} \setminus \{2\}$ lub $D = (-\infty, 2) \cup (2, \infty)$.

Asymptoty Funkcji Wymiernej

Kolejnym ważnym elementem, który pomoże nam zrozumieć zachowanie funkcji wymiernej, są asymptoty. To linie proste, do których wykres funkcji zbliża się w nieskończoność, ale nigdy jej nie osiąga. Wyróżniamy dwa rodzaje asymptot:

Asymptota pionowa: Jest to prosta o równaniu $x=a$, gdzie $a$ jest pierwiastkiem wielomianu $Q(x)$ (czyli wartością wykluczoną z dziedziny), pod warunkiem, że $P(a) \neq 0$. Wartość $x=a$ "ogranicza" dziedzinę, a funkcja "ucieka" do nieskończoności, zbliżając się do tej pionowej linii.
Asymptota pozioma lub ukośna: Zależy ona od stopnia wielomianu licznika ($P(x)$) i mianownika ($Q(x)$).
- Jeśli stopień licznika jest mniejszy niż stopień mianownika, to asymptotą poziomą jest prosta $y=0$ (oś $Ox$).
- Jeśli stopień licznika jest równy stopniowi mianownika, to asymptotą poziomą jest prosta $y=\frac{a_n}{b_m}$, gdzie $a_n$ jest współczynnikiem przy najwyższej potędze $x$ w liczniku, a $b_m$ jest współczynnikiem przy najwyższej potędze $x$ w mianowniku.
- Jeśli stopień licznika jest większy niż stopień mianownika, to funkcja nie ma asymptoty poziomej, ale może mieć asymptotę ukośną. Aby ją znaleźć, dzielimy wielomian $P(x)$ przez $Q(x)$. Wynik dzielenia to wielomian stopnia pierwszego $y=ax+b$, który jest równaniem asymptoty ukośnej.

Przykład (kontynuacja): Dla funkcji $f(x) = \frac{x+1}{x-2}$: * Asymptota pionowa: $x=2$ (ponieważ $x=2$ jest pierwiastkiem mianownika, a licznik w $x=2$ wynosi $2+1=3 \neq 0$). * Stopień licznika (1) jest równy stopniowi mianownika (1). Współczynnik przy $x$ w liczniku to 1, a w mianowniku to 1. Zatem asymptota pozioma to $y=\frac{1}{1}$, czyli $y=1$.

Miejsca Zerowe Funkcji Wymiernej

Miejsca zerowe funkcji to wartości $x$, dla których $f(x)=0$. W przypadku funkcji wymiernej, aby obliczyć miejsca zerowe, musimy przyrównać do zera licznik ($P(x)=0$), jednocześnie pamiętając o dziedzinie. Jeśli pierwiastek licznika należy do dziedziny funkcji, jest on jej miejscem zerowym. Jeśli pierwiastek licznika jest jednocześnie pierwiastkiem mianownika, to nie jest on miejscem zerowym funkcji.

Przykład: Dla funkcji $f(x) = \frac{x^2-4}{x-1}$: * Dziedzina: $x-1 \neq 0 \implies x \neq 1$. $D = \mathbb{R} \setminus \{1\}$. * Miejsca zerowe: Rozwiązujemy $x^2-4 = 0$. Stąd $x^2 = 4$, czyli $x=2$ lub $x=-2$. * Obie wartości, $x=2$ i $x=-2$, należą do dziedziny ($x \neq 1$). Zatem miejsca zerowe to $x=2$ i $x=-2$. * Asymptota pionowa: $x=1$. * Asymptota pozioma: Stopień licznika (2) jest większy od stopnia mianownika (1). Funkcja nie ma asymptoty poziomej, ale ma asymptotę ukośną. Dzielimy $x^2-4$ przez $x-1$. Używając schematu Hornera lub dzielenia pisemnego, otrzymujemy $x+1$ z resztą $-3$. Zatem $f(x) = x+1 - \frac{3}{x-1}$. Asymptota ukośna ma równanie $y=x+1$.

Analiza Wykresu Funkcji Wymiernej

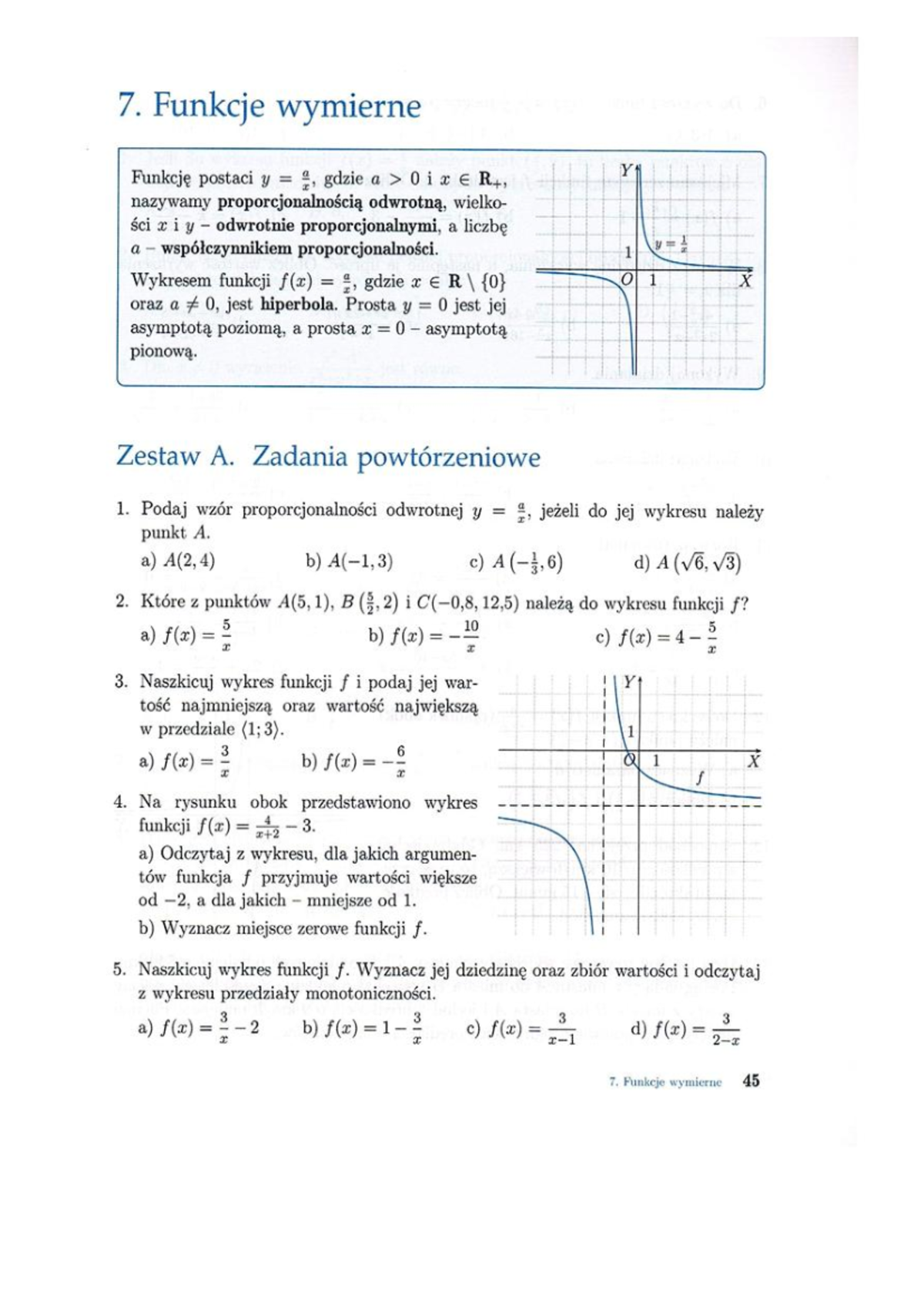
Zrozumienie powyższych elementów – dziedziny, asymptot i miejsc zerowych – pozwala nam na szkicowanie wykresu funkcji wymiernej. Wykres funkcji wymiernej najczęściej składa się z jednej lub więcej gałęzi, które zbliżają się do asymptot. Rozważmy typowy przypadek funkcji homograficznej, czyli funkcji postaci $f(x) = \frac{ax+b}{cx+d}$. Tutaj zawsze występują asymptoty pionowa ($x = -\frac{d}{c}$) i pozioma ($y = \frac{a}{c}$). Wykres funkcji homograficznej to hiperbola, która jest przesunięciem wykresu funkcji $y=\frac{k}{x}$. Wartość $k$ można wyznaczyć, przekształcając wzór funkcji.

Przekształcenia Wykresu Funkcji Wymiernych

Często w zadaniach pojawiają się funkcje wymierne, które są przekształceniami prostszych funkcji. Znając podstawowy wykres i zasady przekształceń, możemy łatwo narysować bardziej złożone funkcje:

Przesunięcie w poziomie: Funkcja $y=f(x-p)$ to wykres funkcji $y=f(x)$ przesunięty o $p$ jednostek w prawo.
Przesunięcie w pionie: Funkcja $y=f(x)+q$ to wykres funkcji $y=f(x)$ przesunięty o $q$ jednostek w górę.
Przekształcenia wykładnicze (odbicia): Funkcja $y=-f(x)$ to odbicie wykresu $y=f(x)$ względem osi $Ox$. Funkcja $y=f(-x)$ to odbicie względem osi $Oy$.

Przykład: Rozważmy funkcję $g(x) = \frac{3}{x-2} + 1$. Jest to funkcja homograficzna, która jest przekształceniem funkcji $y=\frac{3}{x}$. * Dziedzina: $x-2 \neq 0 \implies x \neq 2$. $D = \mathbb{R} \setminus \{2\}$. * Asymptota pionowa: $x=2$. * Asymptota pozioma: $y=1$ (ponieważ funkcja jest przesunięta o 1 w górę od $y=\frac{3}{x}$, której asymptotą poziomą jest $y=0$). * Możemy zauważyć, że $g(x)$ jest funkcją $f(x)=\frac{3}{x}$ przesuniętą o 2 jednostki w prawo i o 1 jednostkę w górę.

Najczęstsze Błędy i Jak Ich Unikać

Podczas rozwiązywania zadań dotyczących funkcji wymiernych, uczniowie często popełniają pewne typowe błędy. Oto kilka z nich i wskazówki, jak ich unikać:

Zapominanie o dziedzinie: To najczęstszy błąd! Zawsze, ale to zawsze, zaczynaj od wyznaczenia dziedziny funkcji. Wartości wykluczone z dziedziny są kluczowe dla zrozumienia zachowania funkcji.
Mylenie asymptot: Upewnij się, że dobrze rozumiesz, kiedy występują asymptoty pionowe, poziome i ukośne, i jak je obliczać w zależności od stopni wielomianów.
Brak sprawdzenia warunku dla miejsc zerowych: Pamiętaj, że miejsce zerowe licznika musi należeć do dziedziny funkcji. Jeśli pierwiastek licznika to ta sama wartość, co pierwiastek mianownika, nie jest to miejsce zerowe.
Błędne przekształcenia wykresów: Dokładnie analizuj, jak konkretne przekształcenia (przesunięcia, odbicia) wpływają na równanie funkcji i jej wykres.

Przykładowe Zadania i Ich Rozwiązania

Aby utrwalić wiedzę, przyjrzyjmy się kilku typowym zadaniom, które mogą pojawić się na sprawdzianie:

Wyznacz dziedzinę, asymptoty i miejsca zerowe funkcji $f(x) = \frac{x-3}{x^2-9}$.
- Dziedzina: $x^2-9 \neq 0 \implies (x-3)(x+3) \neq 0 \implies x \neq 3$ i $x \neq -3$. $D = \mathbb{R} \setminus \{-3, 3\}$.
- Asymptoty: * Pionowe: Chcemy zbadać pierwiastki mianownika. Mamy $x=3$ i $x=-3$. * Dla $x=-3$: Licznik $=-3-3=-6 \neq 0$. Zatem $x=-3$ jest asymptotą pionową. * Dla $x=3$: Licznik $=3-3=0$. Tutaj mamy do czynienia z sytuacją, gdzie mamy wspólny czynnik w liczniku i mianowniku. Zapiszmy funkcję w uproszczonej postaci: $f(x) = \frac{x-3}{(x-3)(x+3)}$. Dla $x \neq 3$, możemy skrócić $(x-3)$, otrzymując $f(x) = \frac{1}{x+3}$. Zatem w $x=3$ nie ma asymptoty pionowej, jest "dziura" w wykresie. * Pozioma: Stopień licznika (1) jest mniejszy od stopnia mianownika (2). Zatem asymptota pozioma to $y=0$.
- Miejsca zerowe: Rozwiązujemy licznik: $x-3=0 \implies x=3$. Jednak $x=3$ jest wykluczone z dziedziny! Zatem funkcja nie ma miejsc zerowych.
Szkicuj wykres funkcji $f(x) = \frac{2x+1}{x-1}$.
- Dziedzina: $x-1 \neq 0 \implies x \neq 1$. $D = \mathbb{R} \setminus \{1\}$.
- Asymptoty: * Pionowa: $x=1$ (ponieważ $x=1$ jest pierwiastkiem mianownika, a licznik w $x=1$ to $2(1)+1=3 \neq 0$). * Pozioma: Stopień licznika (1) jest równy stopniowi mianownika (1). Asymptota pozioma to $y=\frac{2}{1}=2$.
- Miejsca zerowe: $2x+1=0 \implies 2x=-1 \implies x=-\frac{1}{2}$. Ta wartość należy do dziedziny, więc $x=-\frac{1}{2}$ jest miejscem zerowym.
- Dodatkowe punkty: Możemy obliczyć wartość funkcji dla kilku innych argumentów, np. $f(0) = \frac{1}{-1} = -1$. Punkt $(0, -1)$ leży na wykresie.
- Szkic wykresu: Narysuj asymptoty $x=1$ i $y=2$. Zaznacz miejsce zerowe $(-\frac{1}{2}, 0)$ i punkt przecięcia z osią $Oy$ $(0, -1)$. Na podstawie tych informacji, naszkicuj dwie gałęzie hiperboli, które zbliżają się do asymptot.

Podsumowanie i Klucz do Sukcesu

Funkcje wymierne mogą wydawać się na początku skomplikowane, ale z systematycznym podejściem i zrozumieniem kluczowych pojęć, takich jak dziedzina, asymptoty i miejsca zerowe, można je opanować. Pamiętaj o praktyce – im więcej zadań rozwiążesz, tym pewniej będziesz się czuć. Kluczem do sukcesu na sprawdzianie jest dokładność, systematyczność i umiejętność stosowania zdobytej wiedzy w praktyce. Skoncentruj się na każdym kroku analizy funkcji, a wyniki przyjdą same!