Figury Podobne Sprawdzian Z Rozwiazanimi

Witajcie na lekcji poświęconej figurom podobnym! To fascynujący temat, który pozwala nam zrozumieć, jak obiekty mogą mieć ten sam kształt, ale różne rozmiary. Wyobraźcie sobie dwa kwadraty – jeden mały, a drugi duży. Oba są kwadratami, mają cztery kąty proste i cztery równe boki. Właśnie takie obiekty nazywamy figurami podobnymi.
Formalnie, dwie figury są podobne, jeśli istnieje taki proces skalowania (czyli powiększania lub pomniejszania), który pozwala przekształcić jedną figurę w drugą. Kluczowe są tu dwie rzeczy: zachowanie kątów i proporcjonalność boków. Oznacza to, że wszystkie odpowiadające sobie kąty w tych figurach muszą być równe, a stosunek długości odpowiadających sobie boków musi być stały. Ten stały stosunek nazywamy współczynnikiem podobieństwa.
Rozważmy dwa prostokąty. Pierwszy ma boki o długości 2 cm i 4 cm. Drugi ma boki o długości 6 cm i 12 cm. Kąty w obu prostokątach są oczywiście proste (90 stopni), więc warunek kątowy jest spełniony. Sprawdźmy boki. Stosunek dłuższego boku pierwszego prostokąta do dłuższego boku drugiego wynosi 12 cm / 4 cm = 3. Stosunek krótszego boku pierwszego do krótszego boku drugiego to 6 cm / 2 cm = 3. Ponieważ oba stosunki są równe i wynoszą 3, te prostokąty są podobne, a współczynnik podobieństwa wynosi 3 (lub 1/3, jeśli patrzymy z drugiego prostokąta na pierwszy).
Podobieństwo figur ma wiele praktycznych zastosowań. W kartografii mapy są pomniejszonymi wersjami rzeczywistych terenów – są one do nich podobne. W architekturze i projektowaniu modele budynków są zmniejszonymi podobiznami oryginałów. Nawet w sztuce, na przykład przy rysowaniu portretów, artyści często używają technik opartych na podobieństwie, aby zachować proporcje twarzy.
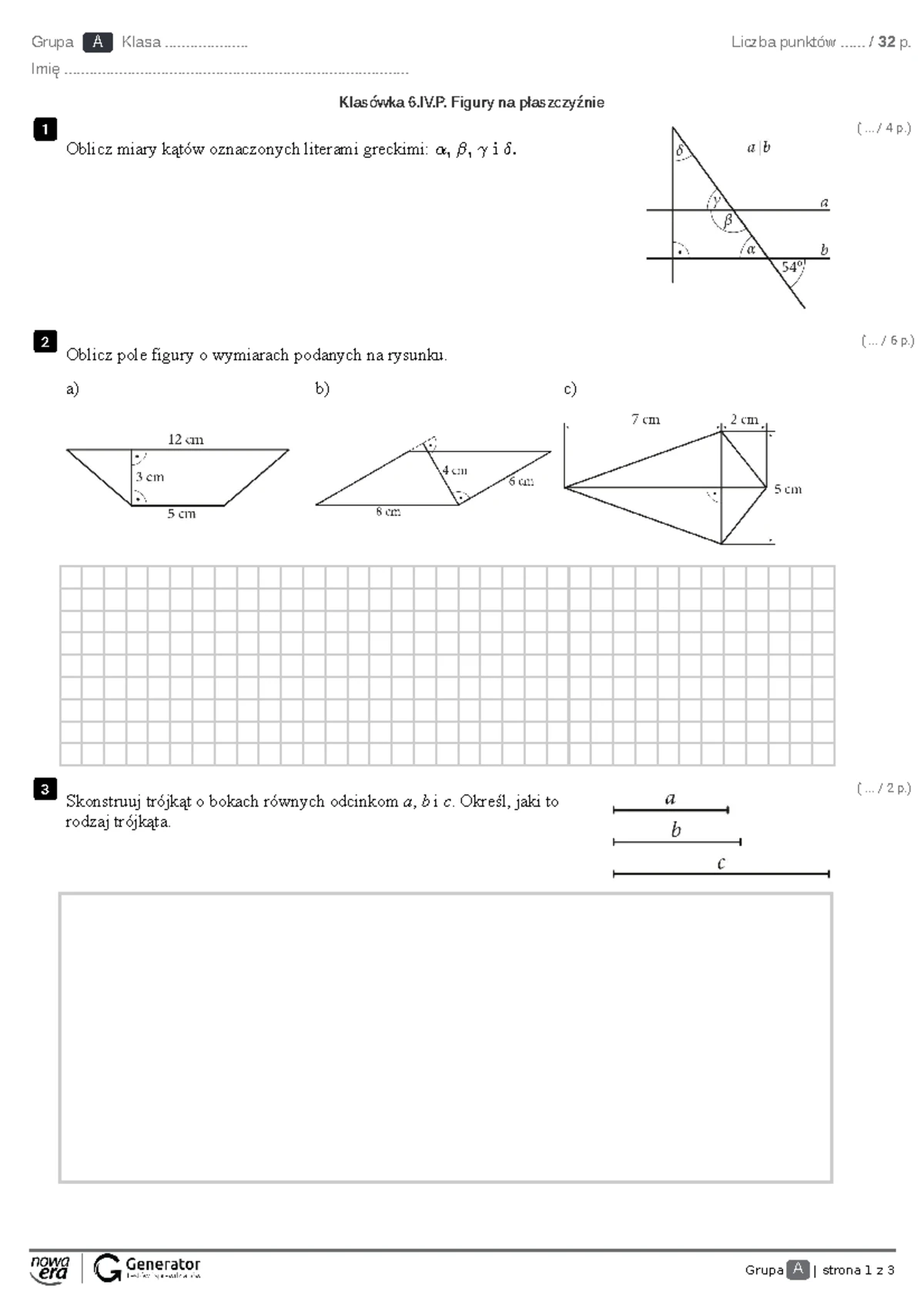
Jeśli chodzi o sprawdziany z tego tematu, zazwyczaj zawierają one zadania wymagające określenia, czy dane figury są podobne, obliczenia brakujących boków lub kątów w figurach podobnych, a także zastosowania tych pojęć w bardziej złożonych problemach. Na przykład, możecie otrzymać zadanie z dwoma trójkątami, gdzie podane są długości kilku boków i kąty, i będziecie musieli udowodnić ich podobieństwo.
Często będziemy musieli obliczyć nieznaną długość boku, korzystając z ustalonego współczynnika podobieństwa. Jeśli wiemy, że dwa trójkąty są podobne i znamy trzy boki jednego i dwa boki drugiego, możemy łatwo obliczyć długość brakującego boku. Wystarczy ustawić odpowiedni proporcję. Pamiętajcie, że zawsze sprawdzamy stosunek odpowiadających sobie boków. To klucz do sukcesu w rozwiązywaniu zadań z figurami podobnymi.
W przypadku rozwiązań do sprawdzianów, kluczowe jest dokładne przedstawienie krok po kroku, jak doszliście do danej odpowiedzi. Zaznaczanie użytych wzorów, wyjaśnianie, dlaczego dany bok odpowiada innemu, oraz jasne podanie ostatecznego wyniku – to wszystko składa się na dobre rozwiązanie. Nie zapominajcie też o jednostkach! Jeśli mamy do czynienia z centymetrami, wynik również powinien być podany w centymetrach.
Praktyczne ćwiczenia, takie jak rysowanie i mierzenie, mogą pomóc w lepszym zrozumieniu pojęcia podobieństwa. Im więcej zadań rozwiążecie, tym łatwiej będzie wam dostrzegać proporcje i stosunki między bokami figur. Powodzenia w dalszej nauce!