Czy kiedykolwiek czułeś się zagubiony, patrząc na liczbę mieszaną i zastanawiając się, jak zamienić ją w ułamek niewłaściwy? Nie jesteś sam! Wiele osób, zarówno dzieci, jak i dorosłych, ma z tym trudności. Matematyka, szczególnie ułamki, może wydawać się początkowo labiryntem, ale z odpowiednim podejściem i zrozumieniem, staje się logiczną i fascynującą dziedziną.
Dlaczego zamiana liczb mieszanych na ułamki niewłaściwe jest ważna?
Zanim przejdziemy do konkretnych metod, warto zrozumieć, dlaczego w ogóle się tym zajmujemy. Ułamki niewłaściwe (gdzie licznik jest większy lub równy mianownikowi) są niezbędne w wielu operacjach matematycznych, takich jak:
- Dodawanie i odejmowanie ułamków: Często łatwiej jest wykonywać te operacje, gdy oba ułamki są w postaci niewłaściwej.
- Mnożenie i dzielenie ułamków: Podobnie jak powyżej, ułamki niewłaściwe upraszczają obliczenia.
- Rozwiązywanie równań: W wielu przypadkach praca z ułamkami niewłaściwymi pozwala na szybsze i bardziej efektywne rozwiązanie równania.
- Zastosowania praktyczne: W kuchni, w budownictwie, w finansach – wszędzie tam, gdzie mamy do czynienia z proporcjami i częściami, ułamki (często niewłaściwe) są na porządku dziennym.
Według badań (np. praca Susan Empson nad rozwojem pojęć ułamkowych u dzieci), solidne zrozumienie ułamków jest kluczowe dla dalszego sukcesu w matematyce. Zaniedbanie tego obszaru może prowadzić do problemów w algebrze, geometrii i innych dziedzinach.
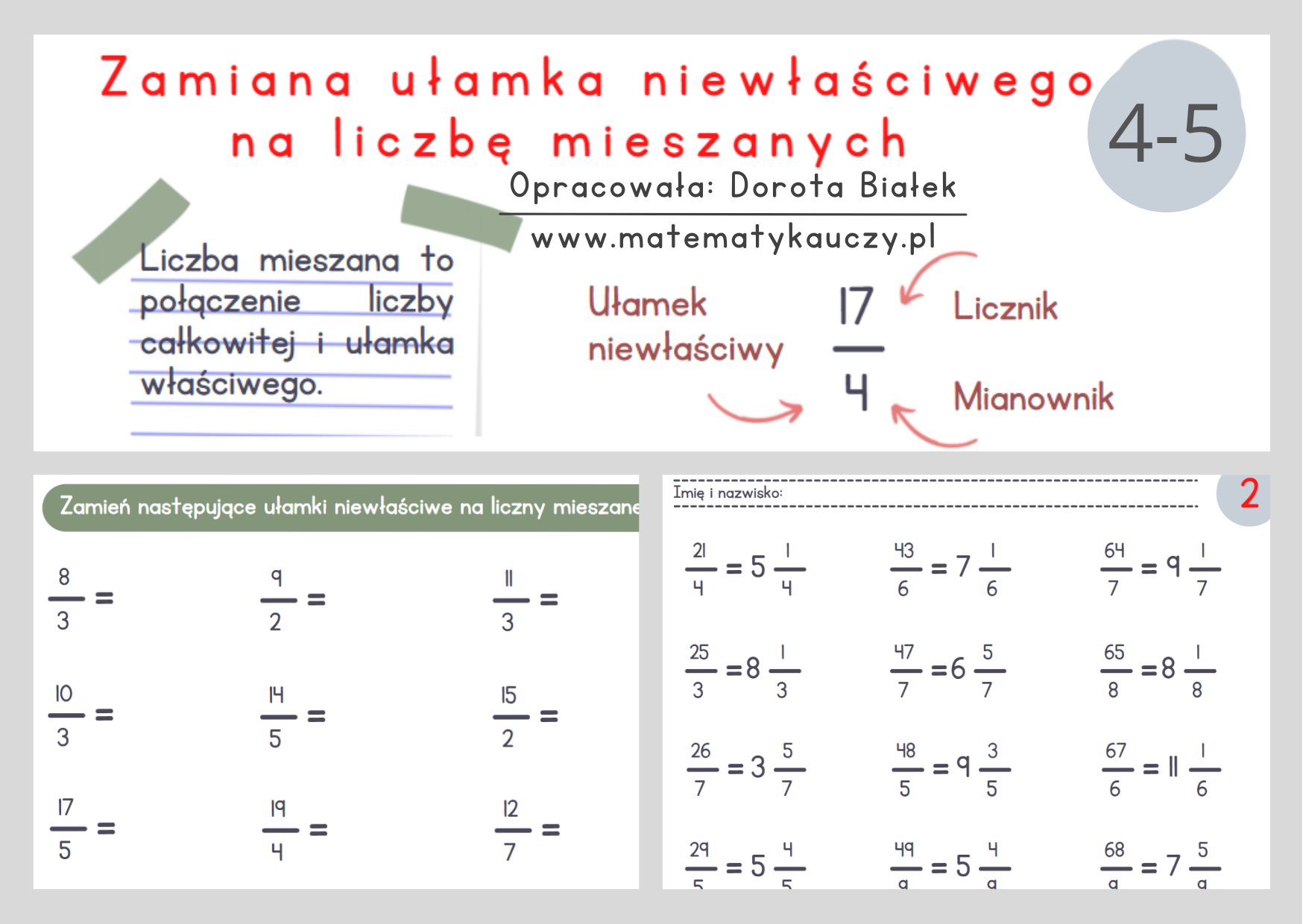
Krok po kroku: Jak zamienić liczbę mieszaną na ułamek niewłaściwy?
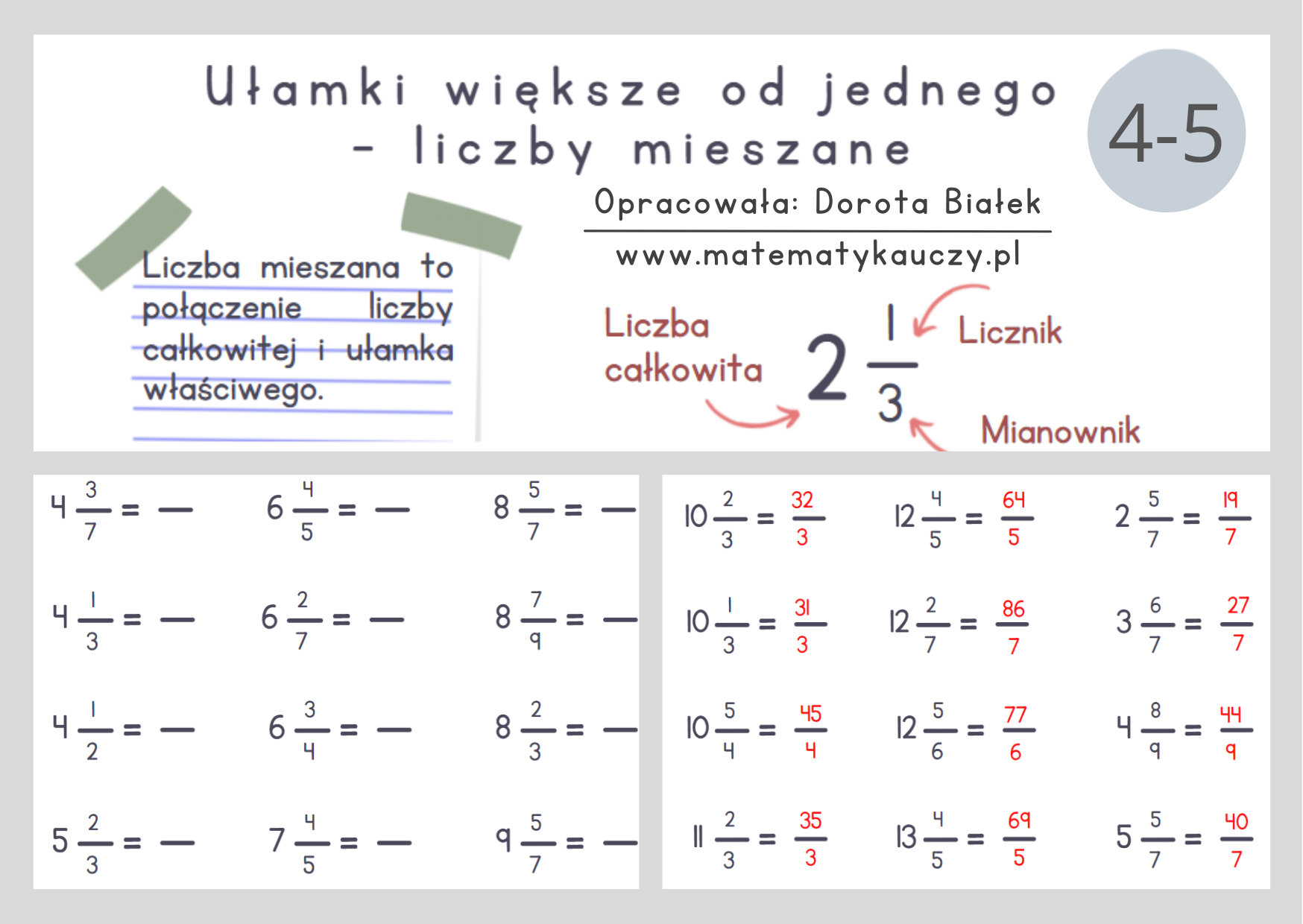
Spójrzmy na konkretny przykład. Załóżmy, że mamy liczbę mieszaną 2 1/3. Oto, co robimy krok po kroku:
Krok 1: Pomnóż liczbę całkowitą przez mianownik.
W naszym przykładzie: 2 * 3 = 6.
Dlaczego to robimy? Pomyśl o liczbie całkowitej jako o pewnej liczbie "całych" kawałków, z których każdy jest podzielony na tyle samo części, ile wskazuje mianownik. W tym przypadku, mamy 2 całe podzielone na 3 części każda, co daje nam 6 części.
Krok 2: Dodaj wynik do licznika.
Teraz dodajemy wynik z kroku 1 do licznika ułamka: 6 + 1 = 7.
Co to oznacza? Dodajemy pozostałą część (licznik) do naszych "całych" kawałków, aby uzyskać całkowitą liczbę części.
Krok 3: Umieść wynik jako licznik, zachowując oryginalny mianownik.
W rezultacie otrzymujemy ułamek niewłaściwy: 7/3.
Dlaczego mianownik pozostaje ten sam? Ponieważ nadal dzielimy całość na te same części (w tym przypadku na 3 części). Zmienia się tylko liczba tych części (czyli licznik).
Przykłady i ćwiczenia
Przećwiczmy to na kilku przykładach:
- 3 2/5: (3 * 5) + 2 = 17. Ułamek niewłaściwy: 17/5
- 1 3/4: (1 * 4) + 3 = 7. Ułamek niewłaściwy: 7/4
- 5 1/2: (5 * 2) + 1 = 11. Ułamek niewłaściwy: 11/2
Spróbuj sam! Zamień następujące liczby mieszane na ułamki niewłaściwe:
- 2 1/4
- 4 2/3
- 1 5/6
(Odpowiedzi: 9/4, 14/3, 11/6)
Metody wizualne i pomoce dydaktyczne
Dla uczniów wizualnych, metody wizualne mogą być niezwykle pomocne. Można użyć:
- Diagramów: Narysuj koła lub prostokąty podzielone na równe części, aby wizualnie reprezentować liczby mieszane i ułamki.
- Manipulacji: Użyj fizycznych przedmiotów, takich jak klocki lub pizza (pokrojona na kawałki!), aby pokazać, jak "całe" mogą być podzielone i połączone z ułamkami.
- Oprogramowania edukacyjnego: Istnieją liczne aplikacje i programy online, które oferują interaktywne ćwiczenia i wizualizacje ułamków.
Wykorzystanie różnych zmysłów (wzrok, dotyk) może znacznie ułatwić zrozumienie i zapamiętanie procesu zamiany liczb mieszanych na ułamki niewłaściwe. Badania pokazują, że nauczanie multisensoryczne poprawia retencję wiedzy i angażuje uczniów w proces uczenia się.
Wskazówki dla nauczycieli i rodziców
Oto kilka praktycznych wskazówek dla nauczycieli i rodziców, którzy chcą pomóc dzieciom w opanowaniu tej umiejętności:
- Zacznij od podstaw: Upewnij się, że dziecko dobrze rozumie pojęcia ułamka, licznika i mianownika.
- Używaj języka zrozumiałego dla dziecka: Unikaj zbyt skomplikowanych terminów i tłumacz wszystko w prosty, przystępny sposób.
- Bądź cierpliwy: Nauka ułamków wymaga czasu i praktyki. Nie zrażaj się, jeśli dziecko nie zrozumie od razu.
- Spraw, by nauka była zabawą: Wykorzystuj gry, zagadki i inne interaktywne metody, aby uczynić naukę ułamków bardziej angażującą.
- Powiąż ułamki z życiem codziennym: Pokaż dziecku, jak ułamki są wykorzystywane w kuchni, w sporcie, w muzyce – wszędzie wokół nas!
- Dostosuj tempo nauki do potrzeb dziecka: Nie spiesz się i nie pomijaj żadnych kroków. Upewnij się, że dziecko w pełni rozumie każdy etap procesu.
- Chwal za wysiłek, a nie tylko za wynik: Ważne jest, aby dziecko czuło się docenione za swoje starania, nawet jeśli popełnia błędy. Pamiętaj, że błędy są naturalną częścią procesu uczenia się.
Pamiętaj: Praktyka czyni mistrza!
Opanowanie zamiany liczb mieszanych na ułamki niewłaściwe, jak każda umiejętność matematyczna, wymaga praktyki. Im więcej ćwiczeń wykonasz, tym łatwiej i szybciej będziesz to robić. Nie bój się popełniać błędów – są one częścią procesu uczenia się.
Z wiarą w siebie i systematyczną pracą, każdy może opanować ułamki i czerpać radość z matematyki. Pamiętaj, matematyka to nie tylko liczby i symbole, to przede wszystkim logiczne myślenie i rozwiązywanie problemów. Powodzenia!