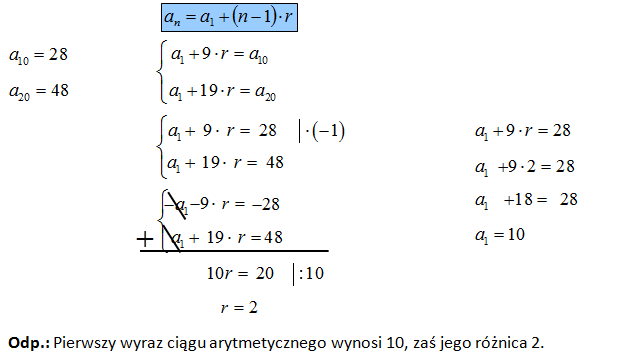Wzór Na środkowy Wyraz Ciągu Arytmetycznego

Czy kiedykolwiek czułeś frustrację, próbując zrozumieć ciągi arytmetyczne? Niby wszystko wydaje się proste na początku, ale nagle pojawia się zadanie, gdzie musisz znaleźć środkowy wyraz, a podręcznik pełen wzorów tylko potęguje chaos? Nie martw się, nie jesteś sam! Wielu uczniów ma podobne trudności. Ten artykuł ma na celu pomóc Ci zrozumieć i opanować wzór na środkowy wyraz ciągu arytmetycznego w sposób prosty i przystępny.

Czym jest Ciąg Arytmetyczny? Krótka Powtórka

Zanim przejdziemy do sedna, upewnijmy się, że dobrze rozumiemy, czym jest ciąg arytmetyczny. Najprościej mówiąc, jest to sekwencja liczb, w której różnica między kolejnymi wyrazami jest stała. Tę stałą różnicę nazywamy różnicą ciągu, oznaczaną zazwyczaj literą 'r'.

Przykłady:

2, 4, 6, 8, 10... (r = 2)
1, 5, 9, 13, 17... (r = 4)
10, 7, 4, 1, -2... (r = -3)

Jak zauważasz, każdy kolejny wyraz otrzymujemy, dodając (lub odejmując, jeśli r jest ujemne) stałą wartość do poprzedniego wyrazu. Kluczowe jest zrozumienie tej zasady, ponieważ stanowi ona fundament do dalszych rozważań.

Wzór na n-ty Wyraz Ciągu Arytmetycznego

Zanim skupimy się na środkowym wyrazie, warto przypomnieć sobie wzór na n-ty wyraz ciągu arytmetycznego. Pozwala on nam znaleźć dowolny wyraz ciągu, znając pierwszy wyraz (a₁) i różnicę (r).

Wzór wygląda następująco:

a_n = a₁ + (n - 1)r

Gdzie:

a_n to n-ty wyraz ciągu
a₁ to pierwszy wyraz ciągu
n to numer wyrazu, który chcemy znaleźć
r to różnica ciągu

Rozważmy przykład. Znajdźmy 10-ty wyraz ciągu arytmetycznego, gdzie a₁ = 3 i r = 2.

a₁₀ = 3 + (10 - 1) * 2 = 3 + 9 * 2 = 3 + 18 = 21

Zatem 10-ty wyraz tego ciągu wynosi 21. Zauważ, że ten wzór jest fundamentem do zrozumienia i wykorzystania wzoru na środkowy wyraz.

Wzór na Środkowy Wyraz Ciągu Arytmetycznego: Upraszczamy Sprawę

Teraz przejdźmy do głównego tematu: wzoru na środkowy wyraz ciągu arytmetycznego. Kluczem jest zrozumienie, że ten wzór dotyczy tylko ciągów o nieparzystej liczbie wyrazów. Dlaczego? Ponieważ tylko wtedy istnieje dokładnie jeden "środkowy" wyraz.

Wzór na środkowy wyraz (a_s) ciągu arytmetycznego o nieparzystej liczbie wyrazów (n) brzmi następująco:

a_s = (a₁ + a_n) / 2

Gdzie:

a_s to środkowy wyraz ciągu
a₁ to pierwszy wyraz ciągu
a_n to ostatni wyraz ciągu

Innymi słowy, środkowy wyraz ciągu arytmetycznego jest średnią arytmetyczną pierwszego i ostatniego wyrazu. To proste, prawda?

Dlaczego to działa? Pomyśl o ciągu arytmetycznym jako o równomiernie rosnącej (lub malejącej) linii. Środek tej linii musi znajdować się dokładnie w połowie drogi między jej początkiem a końcem. Dlatego średnia arytmetyczna pierwszego i ostatniego wyrazu daje nam dokładnie ten środkowy punkt.

Przykłady Użycia Wzoru

Spójrzmy na kilka przykładów, aby utrwalić naszą wiedzę:

Przykład 1:

Dany jest ciąg arytmetyczny: 3, 7, 11, 15, 19. Znajdź środkowy wyraz.

a₁ = 3

a_n = 19

a_s = (3 + 19) / 2 = 22 / 2 = 11

Zatem środkowy wyraz tego ciągu to 11. Jak widzimy, wzór działa! I łatwo to sprawdzić wizualnie.

Przykład 2:

Dany jest ciąg arytmetyczny: 1, 4, 7, 10, 13, 16, 19. Znajdź środkowy wyraz.

a₁ = 1

a_n = 19

a_s = (1 + 19) / 2 = 20 / 2 = 10

Zatem środkowy wyraz tego ciągu to 10. Ponownie, wzór poprawnie wyznaczył środkowy wyraz.

Co zrobić, gdy mamy parzystą liczbę wyrazów?

Wspomnieliśmy, że wzór działa tylko dla ciągów o nieparzystej liczbie wyrazów. Co więc zrobić, gdy mamy ciąg o parzystej liczbie wyrazów?

W takim przypadku nie ma jednego, konkretnego "środkowego" wyrazu. Są dwa wyrazy, które znajdują się w środku ciągu. Aby je znaleźć:

Znajdź liczbę wyrazów (n).
Podziel n przez 2. Wynik oznaczmy jako 'k'.
Wyrazy k-ty i (k+1)-szy to "środkowe" wyrazy.

Np. dla ciągu 2, 4, 6, 8, mamy n = 4. Zatem k = 4 / 2 = 2. Wyrazy drugi i trzeci (4 i 6) są "środkowymi" wyrazami.

W wielu zadaniach będziesz musiał obliczyć średnią arytmetyczną tych dwóch środkowych wyrazów. W naszym przykładzie: (4 + 6) / 2 = 5.

Dlaczego Warto Znać Ten Wzór?

Wzór na środkowy wyraz ciągu arytmetycznego, choć wydaje się prosty, jest bardzo użyteczny w wielu sytuacjach. Oto kilka powodów, dla których warto go znać:

Szybsze rozwiązywanie zadań: Zamiast wypisywać cały ciąg, możesz od razu obliczyć środkowy wyraz, oszczędzając czas na egzaminach.
Zrozumienie natury ciągów arytmetycznych: Wzór ten pomaga lepiej zrozumieć, jak zbudowane są ciągi arytmetyczne i jak powiązane są ze sobą ich wyrazy.
Podstawa do dalszej nauki: Zrozumienie ciągów arytmetycznych jest niezbędne do dalszej nauki matematyki, np. szeregów arytmetycznych.

Potwierdzeniem wartości tego wzoru są liczne podręczniki i materiały edukacyjne, w których jest on szeroko omawiany. Nauczyciele często podkreślają jego znaczenie, zachęcając uczniów do jego zapamiętania i stosowania.

Praktyczne Porady i Narzędzia

Oto kilka praktycznych porad, które pomogą Ci lepiej opanować wzór na środkowy wyraz ciągu arytmetycznego:

Ćwicz regularnie: Rozwiązuj jak najwięcej zadań, aby utrwalić swoją wiedzę.
Używaj kalkulatora: Kalkulator może pomóc Ci w obliczeniach, szczególnie gdy masz do czynienia z dużymi liczbami.
Twórz własne przykłady: Wymyślaj własne ciągi arytmetyczne i obliczaj ich środkowe wyrazy.
Szukaj pomocy: Jeśli masz trudności, nie wstydź się pytać nauczyciela, kolegów lub szukać informacji w internecie.

Dostępne są również narzędzia online, które mogą pomóc Ci w nauce ciągów arytmetycznych. Możesz znaleźć kalkulatory, które automatycznie obliczają środkowy wyraz, lub interaktywne lekcje, które pomogą Ci zrozumieć koncepcję.

Podsumowanie

Wzór na środkowy wyraz ciągu arytmetycznego jest prostym, ale potężnym narzędziem, które może znacznie ułatwić rozwiązywanie zadań z ciągów. Pamiętaj, aby dobrze zrozumieć definicję ciągu arytmetycznego i wzór na n-ty wyraz, zanim zaczniesz używać wzoru na środkowy wyraz. Regularne ćwiczenia i korzystanie z dostępnych narzędzi pomogą Ci opanować tę umiejętność i wykorzystać ją w praktyce.

Pamiętaj: matematyka to nie tylko suche wzory, to przede wszystkim logiczne myślenie i rozwiązywanie problemów. Im lepiej zrozumiesz zasady, tym łatwiej będzie Ci radzić sobie z trudniejszymi zadaniami. Powodzenia!