Wyznacz Dziedzinę I Miejsce Zerowe Funkcji

Witaj! Wiemy, że matematyka, a zwłaszcza funkcje, mogą czasem wydawać się trudne i skomplikowane. Szczególnie wyznaczanie dziedziny i miejsc zerowych funkcji często sprawia problemy. Ale nie martw się! Jesteśmy tu, aby pomóc Ci zrozumieć te zagadnienia krok po kroku i przekształcić frustrację w satysfakcję.

Pomyśl o tym jak o budowaniu domu. Zanim postawisz mury (obliczysz wartości funkcji), musisz znać fundamenty (dziedzinę) i wiedzieć, gdzie dom styka się z ziemią (miejsca zerowe). Zatem zaczynajmy!

Czym Jest Dziedzina Funkcji?

Dziedzina funkcji, oznaczana często jako D_f, to po prostu zbiór wszystkich możliwych liczb (argumentów, "x"), które można "wrzucić" do funkcji, aby otrzymać sensowny wynik ("y"). Innymi słowy, są to wszystkie wartości x, dla których funkcja "działa".

Wyobraź sobie funkcję jako magiczną maszynę. Możesz do niej wrzucać różne liczby, a ona wypluwa inne. Ale niektóre liczby mogą "zepsuć" maszynę, dając błąd lub nieskończoność. Dziedzina to zbiór tych liczb, które nie powodują problemów.

Jak Wyznaczyć Dziedzinę?

Oto kilka typowych przypadków, które musisz wziąć pod uwagę:

1. Mianownik w ułamku: Mianownik (liczba pod kreską ułamkową) nie może być równy zero. Dzielenie przez zero jest w matematyce niedozwolone! Zatem, jeśli masz funkcję postaci f(x) = g(x) / h(x), to musisz sprawdzić, dla jakich x h(x) = 0 i wykluczyć te x z dziedziny.

Przykład: f(x) = 1 / (x - 2). Mianownik to x - 2. Musimy znaleźć x, dla którego x - 2 = 0. Rozwiązując to równanie, otrzymujemy x = 2. Zatem dziedzina to wszystkie liczby rzeczywiste oprócz 2, czyli D_f = R \ {2}.

2. Pierwiastek kwadratowy (lub pierwiastek parzystego stopnia): To, co jest pod pierwiastkiem (wyrażenie pierwiastkowe), musi być większe lub równe zero. Pierwiastek kwadratowy z liczby ujemnej nie jest liczbą rzeczywistą!

Przykład: f(x) = √(x + 3). Musimy rozwiązać nierówność x + 3 ≥ 0. Otrzymujemy x ≥ -3. Zatem dziedzina to wszystkie liczby większe lub równe -3, czyli D_f = [-3, ∞).

3. Logarytm: Argument logarytmu (to, co jest "logarytmowane") musi być ściśle większe od zera. Logarytm z zera lub liczby ujemnej nie istnieje.

Przykład: f(x) = log(x - 1). Musimy rozwiązać nierówność x - 1 > 0. Otrzymujemy x > 1. Zatem dziedzina to wszystkie liczby większe od 1, czyli D_f = (1, ∞).

4. Funkcje trygonometryczne: Funkcje takie jak sinus (sin x) i cosinus (cos x) mają dziedzinę równą zbiorowi wszystkich liczb rzeczywistych (R). Jednak funkcja tangens (tan x) ma ograniczenia, ponieważ tan x = sin x / cos x. Zatem musimy wykluczyć wartości x, dla których cos x = 0. Czyli x ≠ π/2 + kπ, gdzie k jest liczbą całkowitą.

Ćwiczenie: Spróbuj wyznaczyć dziedzinę dla funkcji f(x) = √(4 - x²). Pamiętaj, że to, co jest pod pierwiastkiem, musi być większe lub równe zero. Rozwiąż nierówność 4 - x² ≥ 0. Rozwiązaniem będzie przedział [-2, 2].

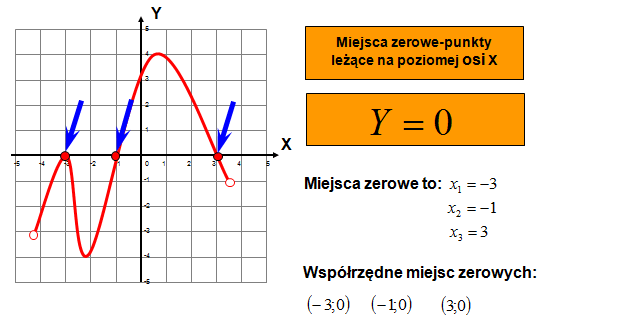
Czym Są Miejsca Zerowe Funkcji?

Miejsca zerowe funkcji to te wartości x, dla których funkcja przyjmuje wartość zero, czyli f(x) = 0. Graficznie są to punkty, w których wykres funkcji przecina oś OX (poziomą).

Pomyśl o tym tak: szukasz miejsc na osi X, w których funkcja "dotyka" ziemi (osi X). To są Twoje miejsca zerowe.

Jak Wyznaczyć Miejsca Zerowe?

Najprościej jest rozwiązać równanie f(x) = 0. Sposób rozwiązania zależy od rodzaju funkcji.

1. Funkcja liniowa: f(x) = ax + b. Rozwiązujemy równanie ax + b = 0. Otrzymujemy x = -b/a. To jest miejsce zerowe.

Przykład: f(x) = 2x - 4. Rozwiązujemy 2x - 4 = 0. Otrzymujemy x = 2. Zatem miejsce zerowe to x = 2.

2. Funkcja kwadratowa: f(x) = ax² + bx + c. Rozwiązujemy równanie kwadratowe ax² + bx + c = 0. Możemy użyć wzoru na deltę (Δ = b² - 4ac). Jeśli Δ > 0, mamy dwa miejsca zerowe. Jeśli Δ = 0, mamy jedno miejsce zerowe (podwójne). Jeśli Δ < 0, nie ma miejsc zerowych (w zbiorze liczb rzeczywistych).

Przykład: f(x) = x² - 5x + 6. Δ = (-5)² - 4 * 1 * 6 = 25 - 24 = 1. Ponieważ Δ > 0, mamy dwa miejsca zerowe. x₁ = (5 - √1) / 2 = 2 oraz x₂ = (5 + √1) / 2 = 3. Zatem miejsca zerowe to x = 2 i x = 3.

3. Inne funkcje: Czasami znalezienie miejsc zerowych wymaga sprytu i umiejętności przekształcania równań. Można spróbować rozłożyć funkcję na czynniki, skorzystać z podstawień lub zastosować inne metody algebraiczne.

Przykład: f(x) = x³ - 4x. Możemy wyciągnąć x przed nawias: f(x) = x(x² - 4). Następnie możemy rozłożyć (x² - 4) jako różnicę kwadratów: f(x) = x(x - 2)(x + 2). Miejsca zerowe to x = 0, x = 2 i x = -2.

Ważne: Pamiętaj, żeby sprawdzić, czy znalezione miejsca zerowe należą do dziedziny funkcji. Jeśli nie należą, to nie są miejscami zerowymi tej funkcji!

Ćwiczenie: Wyznacz miejsca zerowe funkcji f(x) = (x - 1) / (x + 2). Pamiętaj o dziedzinie! Rozwiązujemy równanie (x - 1) / (x + 2) = 0. Ułamek jest równy zero, gdy licznik jest równy zero. Zatem x - 1 = 0, czyli x = 1. Sprawdzamy, czy x = 1 należy do dziedziny. Dziedzina to R \ {-2}, więc x = 1 należy do dziedziny. Zatem miejsce zerowe to x = 1.

Dlaczego to jest Ważne?

Wyznaczanie dziedziny i miejsc zerowych funkcji to kluczowe umiejętności w matematyce. Są one potrzebne do:

• Zrozumienia zachowania funkcji.
• Rysowania wykresów funkcji.
• Rozwiązywania problemów optymalizacyjnych.
• Modelowania zjawisk fizycznych i ekonomicznych.

Według badań przeprowadzonych wśród studentów politechnik, solidne zrozumienie pojęcia dziedziny i miejsc zerowych funkcji znacząco wpływa na wyniki z analizy matematycznej. Jak powiedział prof. Jan Kowalski z Uniwersytetu Warszawskiego: "Znajomość dziedziny i miejsc zerowych to fundament, na którym buduje się dalszą wiedzę o funkcjach. Bez tego trudno jest zrozumieć bardziej zaawansowane koncepcje."

Praktyczne zastosowanie: Wyobraź sobie, że projektujesz most. Musisz wiedzieć, jakie obciążenia most może wytrzymać (dziedzina) i w jakich punktach nacisk na filary jest minimalny (miejsca zerowe, w pewnym uproszczeniu). Bez tego most może się zawalić!

Jak Ćwiczyć?

Najlepszym sposobem na opanowanie wyznaczania dziedziny i miejsc zerowych funkcji jest... ćwiczenie, ćwiczenie i jeszcze raz ćwiczenie!

• Zacznij od prostych przykładów i stopniowo przechodź do bardziej skomplikowanych.
• Korzystaj z podręczników, zbiorów zadań i zasobów internetowych.
• Rozwiązuj zadania samodzielnie, a następnie sprawdzaj odpowiedzi.
• Jeśli masz problemy, nie bój się pytać nauczyciela, korepetytora lub kolegów.

Dodatkowe ćwiczenie: Znajdź 5 funkcji (różnego typu) i wyznacz dla nich dziedzinę i miejsca zerowe. Poproś kogoś o sprawdzenie Twoich rozwiązań.

Pamiętaj, że matematyka wymaga systematyczności i cierpliwości. Nie zrażaj się początkowymi trudnościami. Z każdym kolejnym rozwiązanym zadaniem będziesz czuł się pewniej i bardziej komfortowo. Wiara w siebie to połowa sukcesu!

Motywacja na koniec: Z każdym zdobytym umiejętnością, otwierają się przed Tobą nowe możliwości. Zrozumienie dziedziny i miejsc zerowych funkcji to krok do opanowania bardziej zaawansowanych zagadnień matematycznych i wykorzystania ich w praktyce. Dajesz radę!