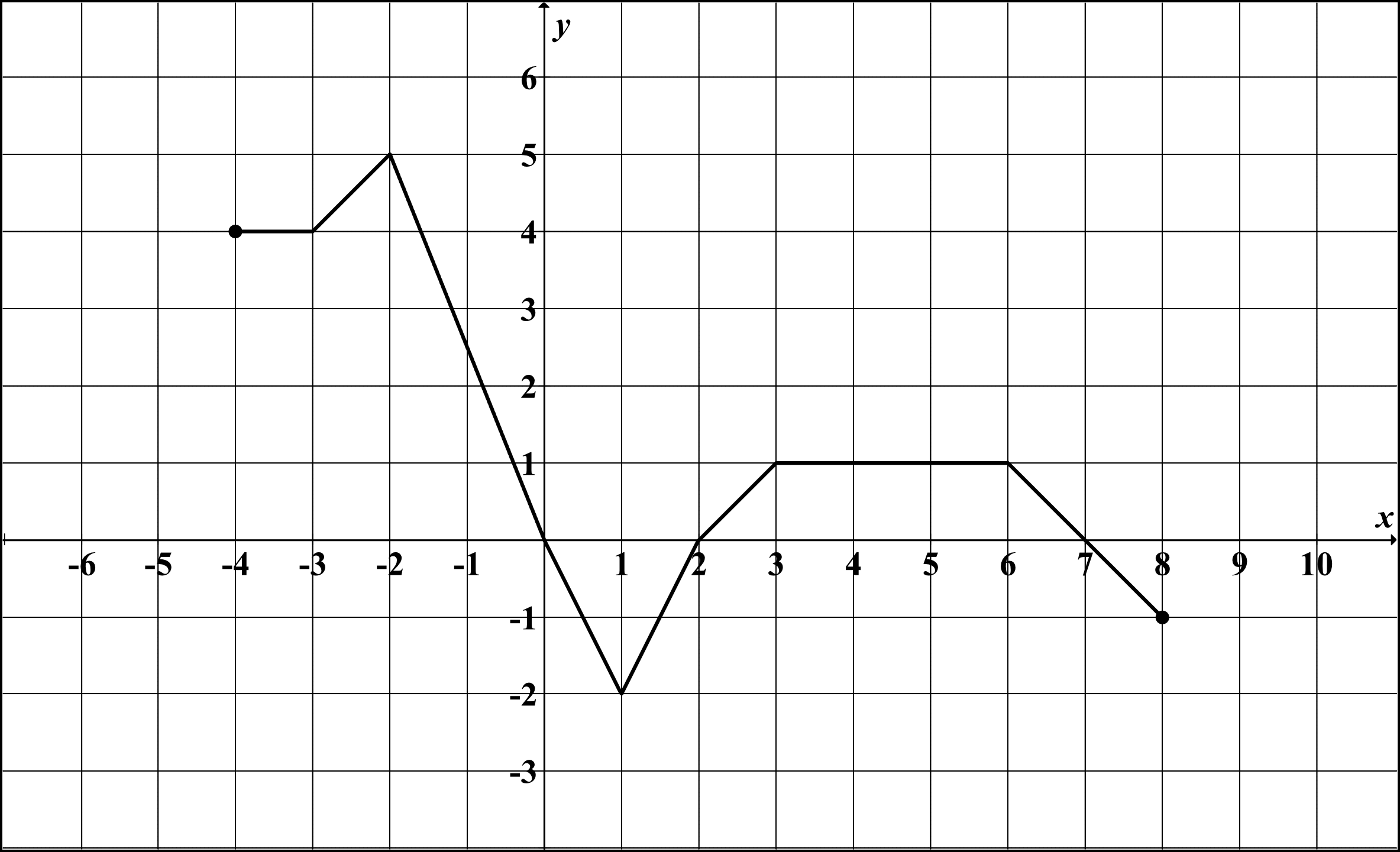
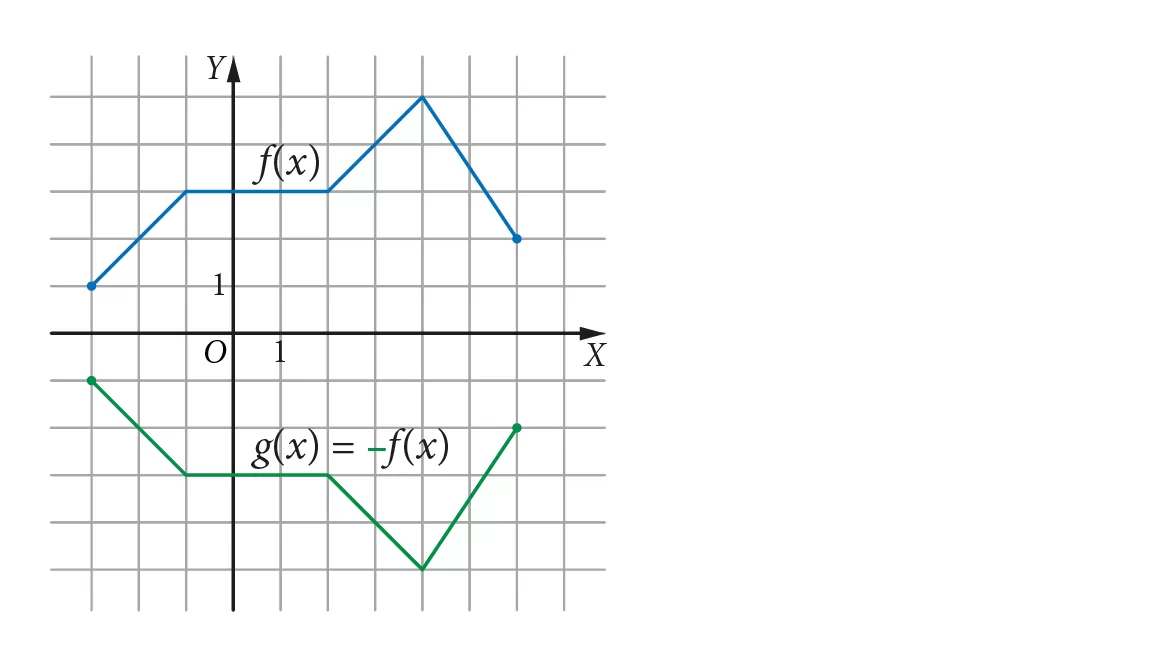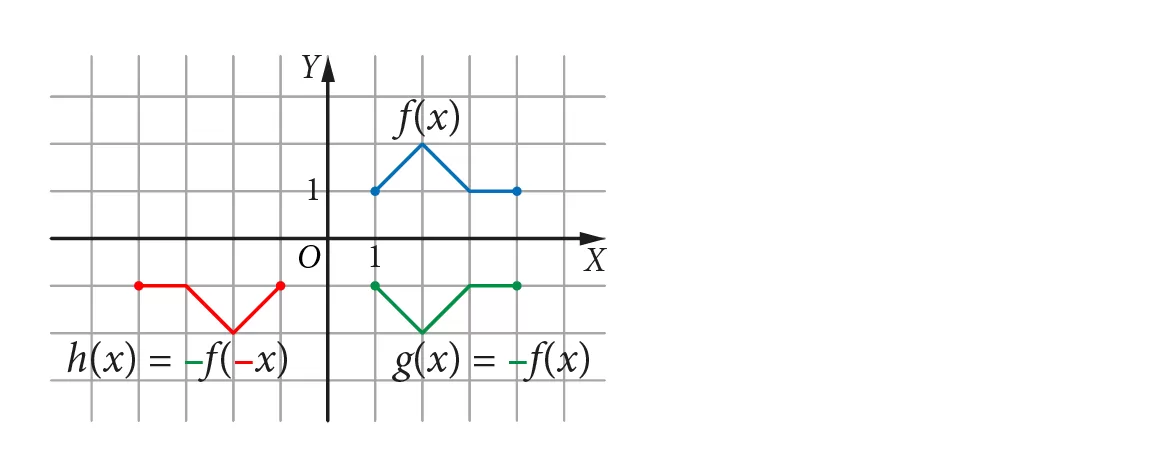Czy kiedykolwiek patrząc na wykres funkcji pomyślałeś: "Jak mogę go zmodyfikować, aby uzyskać zupełnie nowy wykres, zachowując jednocześnie pewne podstawowe cechy"? A może masz dane, które wyglądają prawie jak znana funkcja, ale są odbite lub odwrócone? W tym artykule przyjrzymy się, jak symetrie względem osi i punktu mogą nam pomóc w transformacji wykresów funkcji i zrozumieniu ich właściwości. Zrozumienie tych transformacji jest kluczowe nie tylko w matematyce, ale także w fizyce, informatyce i wielu innych dziedzinach.
Symetria względem osi OX (osi x)
Wyobraź sobie, że masz wykres funkcji f(x). Chcesz go odbić względem osi OX. Jak to zrobić? Odpowiedź jest prosta: zmień znak wartości funkcji.
Oznacza to, że nowa funkcja, g(x), będzie zdefiniowana jako:
g(x) = -f(x)
Co to oznacza w praktyce? Każdy punkt (x, y) na wykresie f(x) zostanie przekształcony w punkt (x, -y) na wykresie g(x). Na przykład, jeśli f(2) = 3, to g(2) = -3. Wykres funkcji g(x) będzie lustrzanym odbiciem wykresu funkcji f(x) względem osi OX.
Przykład:
Załóżmy, że f(x) = x². Wtedy g(x) = -x². Wykres f(x) to parabola skierowana w górę, natomiast wykres g(x) to parabola skierowana w dół. Oba wykresy są symetryczne względem osi OX.
Praktyczne zastosowanie: Ta transformacja jest używana w fizyce, na przykład do odwracania potencjału elektrycznego. Jeśli mamy potencjał V(x), to -V(x) reprezentuje potencjał o przeciwnym znaku.
Symetria względem osi OY (osi y)
Teraz zastanówmy się, jak odbić wykres funkcji względem osi OY. Tym razem zmieniamy znak argumentu funkcji.
Nowa funkcja g(x) będzie zdefiniowana jako:
g(x) = f(-x)
Jak to wpływa na wykres? Każdy punkt (x, y) na wykresie f(x) zostanie przekształcony w punkt (-x, y) na wykresie g(x). Jeśli f(3) = 5, to g(-3) = 5. Wykres funkcji g(x) będzie lustrzanym odbiciem wykresu funkcji f(x) względem osi OY.
Przykład:
Rozważmy funkcję f(x) = ex. Wtedy g(x) = e-x. Wykres f(x) to funkcja rosnąca, natomiast wykres g(x) to funkcja malejąca. Oba wykresy są symetryczne względem osi OY.
Funkcje parzyste: Szczególnym przypadkiem są funkcje parzyste, dla których zachodzi f(x) = f(-x). Oznacza to, że wykres funkcji parzystej jest symetryczny względem osi OY. Przykłady to x², cos(x).
Praktyczne zastosowanie: W przetwarzaniu sygnałów, odbicie sygnału w czasie jest opisywane przez tę transformację. Jeśli mamy sygnał s(t), to s(-t) reprezentuje sygnał odwrócony w czasie.
Symetria względem początku układu współrzędnych (punktu (0,0))
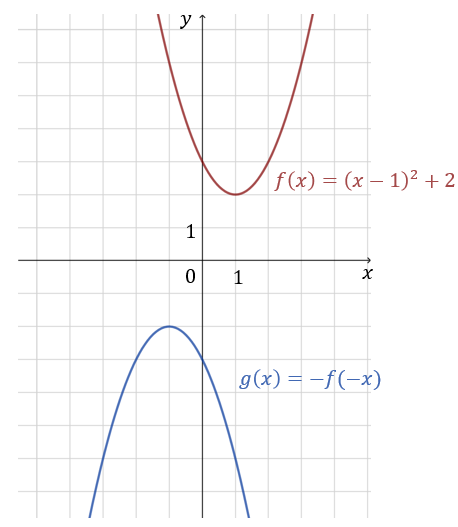
Ostatnim rodzajem symetrii, który omówimy, jest symetria względem początku układu współrzędnych. W tym przypadku zmieniamy znak zarówno wartości funkcji, jak i jej argumentu.
Nowa funkcja g(x) będzie zdefiniowana jako:
g(x) = -f(-x)
Co to oznacza na wykresie? Każdy punkt (x, y) na wykresie f(x) zostanie przekształcony w punkt (-x, -y) na wykresie g(x). Jeśli f(4) = 2, to g(-4) = -2. Wykres funkcji g(x) jest wynikiem dwukrotnego odbicia: najpierw względem osi OY, a następnie względem osi OX (lub odwrotnie).
Przykład:
Weźmy funkcję f(x) = x³. Wtedy g(x) = -(-x)³ = x³. W tym przypadku f(x) = g(x), co oznacza, że funkcja x³ jest symetryczna względem początku układu współrzędnych.
Funkcje nieparzyste: Funkcje, które spełniają warunek f(x) = -f(-x), nazywamy funkcjami nieparzystymi. Ich wykresy są symetryczne względem początku układu współrzędnych. Przykłady to x³, sin(x).
Praktyczne zastosowanie: W fizyce, symetria względem początku układu współrzędnych jest ważna w teorii pola, np. przy analizie pól wektorowych i tensorowych. Często pozwala uprościć obliczenia i zrozumieć fundamentalne własności tych pól.
Pamiętaj!
- Symetria względem osi OX: g(x) = -f(x)
- Symetria względem osi OY: g(x) = f(-x)
- Symetria względem początku układu: g(x) = -f(-x)
Dlaczego symetrie są ważne?
Zrozumienie symetrii funkcji ma ogromne znaczenie z kilku powodów:
- Upraszczają analizę: Znając symetrię funkcji, możemy skupić się na analizie tylko jednej części wykresu, a resztę możemy odtworzyć na podstawie symetrii.
- Ułatwiają rozwiązywanie równań: W niektórych przypadkach symetria pozwala uprościć rozwiązywanie równań, szczególnie równań różniczkowych.
- Pomagają w modelowaniu zjawisk: W wielu dziedzinach nauki i inżynierii, symetria jest fundamentalną własnością modelowanych zjawisk.
- Zrozumienie podstawowych własności funkcji: Rozróżnianie funkcji parzystych i nieparzystych jest kluczowe w wielu obliczeniach i analizach matematycznych.
Badania pokazują, że uczniowie, którzy rozumieją koncepcję symetrii funkcji, lepiej radzą sobie z rozwiązywaniem problemów matematycznych i mają głębsze zrozumienie pojęcia funkcji (źródło: badania dydaktyczne nad nauczaniem funkcji).
Podsumowanie
Przekształcanie wykresów funkcji poprzez symetrię to potężne narzędzie, które pozwala na lepsze zrozumienie i manipulowanie funkcjami. Niezależnie od tego, czy jesteś studentem, inżynierem, czy po prostu osobą ciekawą świata matematyki, zrozumienie tych koncepcji może otworzyć drzwi do głębszego zrozumienia otaczającej nas rzeczywistości. Pamiętaj o kluczowych transformacjach: zmiana znaku wartości funkcji dla symetrii względem osi OX, zmiana znaku argumentu funkcji dla symetrii względem osi OY i zmiana znaku obu dla symetrii względem początku układu współrzędnych. Ćwicz regularnie z różnymi przykładami, a wkrótce przekonasz się, jak bardzo te transformacje mogą ułatwić Twoją pracę!