W Jednorodnym Polu Magnetycznym O Indukcji

Ruch ładunku w jednorodnym polu magnetycznym o indukcji odnosi się do ruchu naładowanej cząstki, takiej jak elektron lub proton, w obszarze, w którym indukcja magnetyczna (oznaczana przez B) ma stałą wartość i kierunek w każdym punkcie przestrzeni.
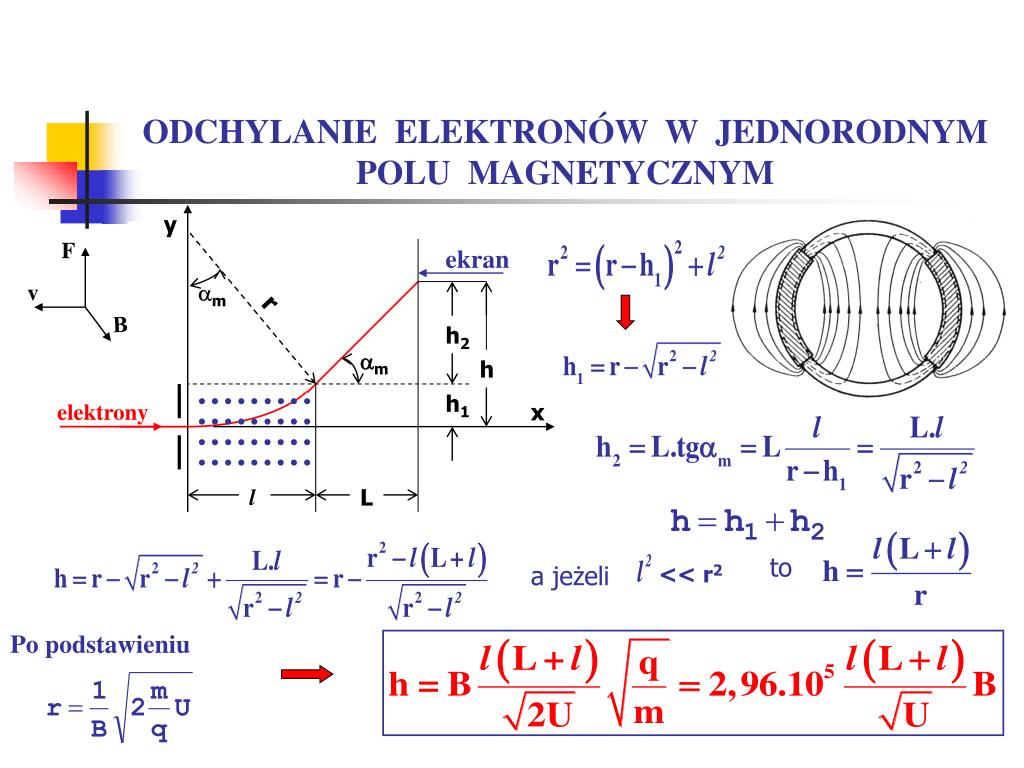
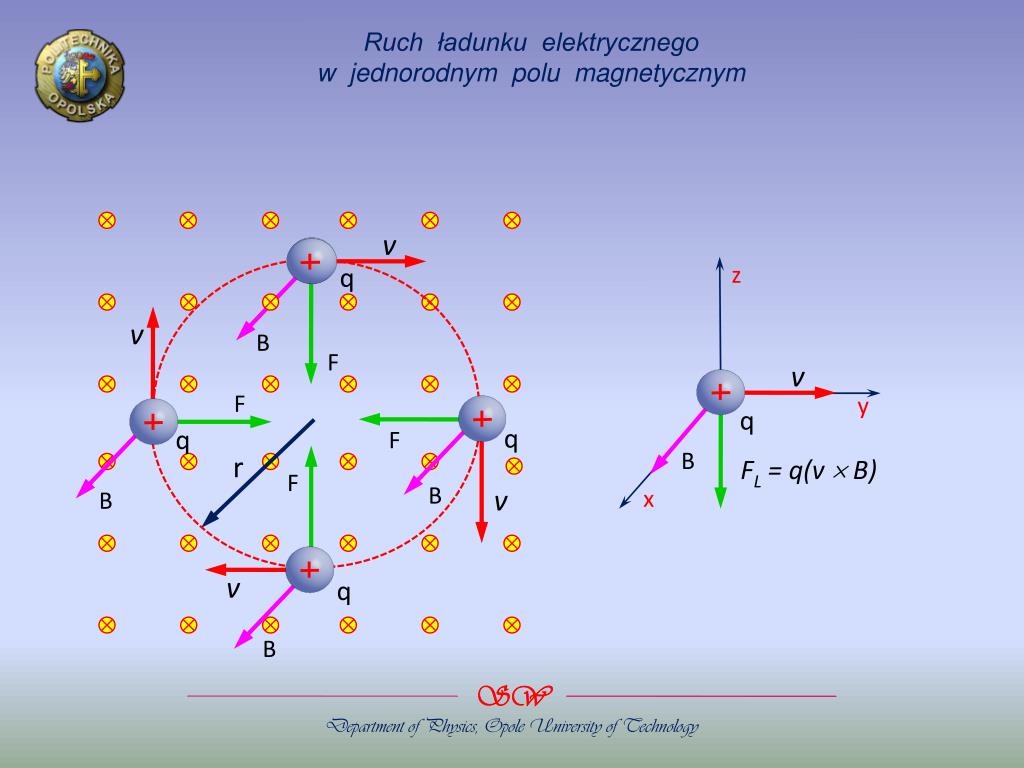
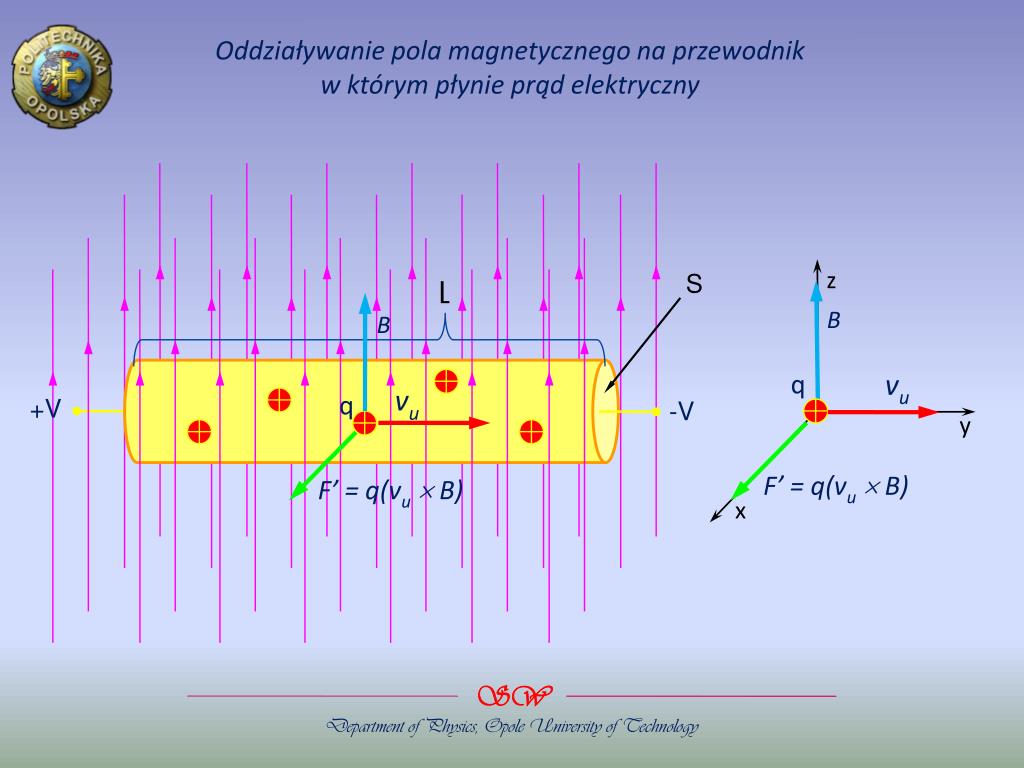
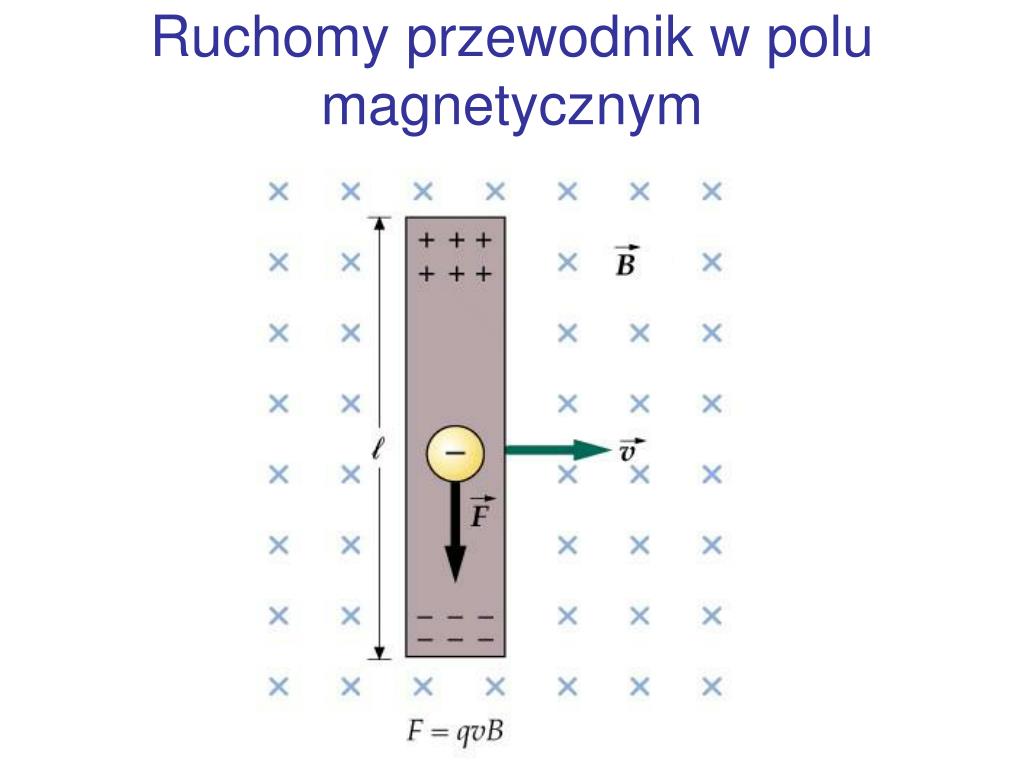
Aby zrozumieć ten ruch, rozważmy naładowaną cząstkę (o ładunku q) poruszającą się z prędkością v w jednorodnym polu magnetycznym B. Działa na nią siła Lorentza, określona wzorem: F = q(v x B). Oznacza to, że siła jest proporcjonalna do ładunku, prędkości i indukcji magnetycznej, a jej kierunek jest prostopadły zarówno do prędkości, jak i do pola magnetycznego.
Krok 1: Kierunek ruchu prostopadły do pola. Załóżmy, że prędkość cząstki jest prostopadła do kierunku pola magnetycznego. Wtedy siła Lorentza jest zawsze prostopadła do prędkości, co powoduje, że cząstka zaczyna poruszać się po okręgu. Promień okręgu (r) zależy od masy (m), prędkości (v), ładunku (q) i indukcji magnetycznej (B), i można go obliczyć ze wzoru: r = mv / (qB). Im większa masa lub prędkość, tym większy promień. Im większy ładunek lub indukcja magnetyczna, tym mniejszy promień.
Przykład: Elektron (q = -1.6 x 10-19 C, m = 9.11 x 10-31 kg) porusza się z prędkością 106 m/s prostopadle do pola magnetycznego o indukcji 1 T. Promień orbity wyniesie r = (9.11 x 10-31 kg * 106 m/s) / (1.6 x 10-19 C * 1 T) ≈ 5.7 x 10-6 m.
Krok 2: Kierunek ruchu pod kątem do pola. Jeśli prędkość cząstki nie jest prostopadła do pola magnetycznego, to możemy ją rozłożyć na dwie składowe: v|| (równoległą do B) i v⊥ (prostopadłą do B). Składowa v|| pozostaje niezmieniona, ponieważ siła magnetyczna na nią nie działa. Składowa v⊥ powoduje ruch po okręgu, jak opisano w Kroku 1. W rezultacie cząstka porusza się po linii śrubowej (helisie) wzdłuż linii pola magnetycznego.
Przykład: Proton wpada do pola magnetycznego pod kątem 30 stopni. Będzie poruszał się po helisie, której promień zależy od składowej prędkości prostopadłej do pola, a skok helisy (odległość, jaką cząstka pokonuje wzdłuż linii pola magnetycznego podczas jednego obrotu) zależy od składowej równoległej do pola.
Krok 3: Energia kinetyczna. Praca wykonywana przez siłę Lorentza jest zawsze równa zeru, ponieważ siła jest zawsze prostopadła do przemieszczenia. Oznacza to, że energia kinetyczna cząstki pozostaje stała. Pole magnetyczne zmienia jedynie kierunek prędkości, ale nie jej wartość.
Praktyczne zastosowania: Jednym z ważnych zastosowań jest spektrometria masowa, gdzie analizuje się stosunek masy do ładunku jonów. Iony o różnym stosunku m/q poruszają się po okręgach o różnych promieniach w jednorodnym polu magnetycznym, co pozwala na ich separację i identyfikację. Innym zastosowaniem są akceleratory cząstek, gdzie pola magnetyczne służą do zakrzywiania toru cząstek naładowanych i utrzymywania ich w obrębie akceleratora podczas przyspieszania.