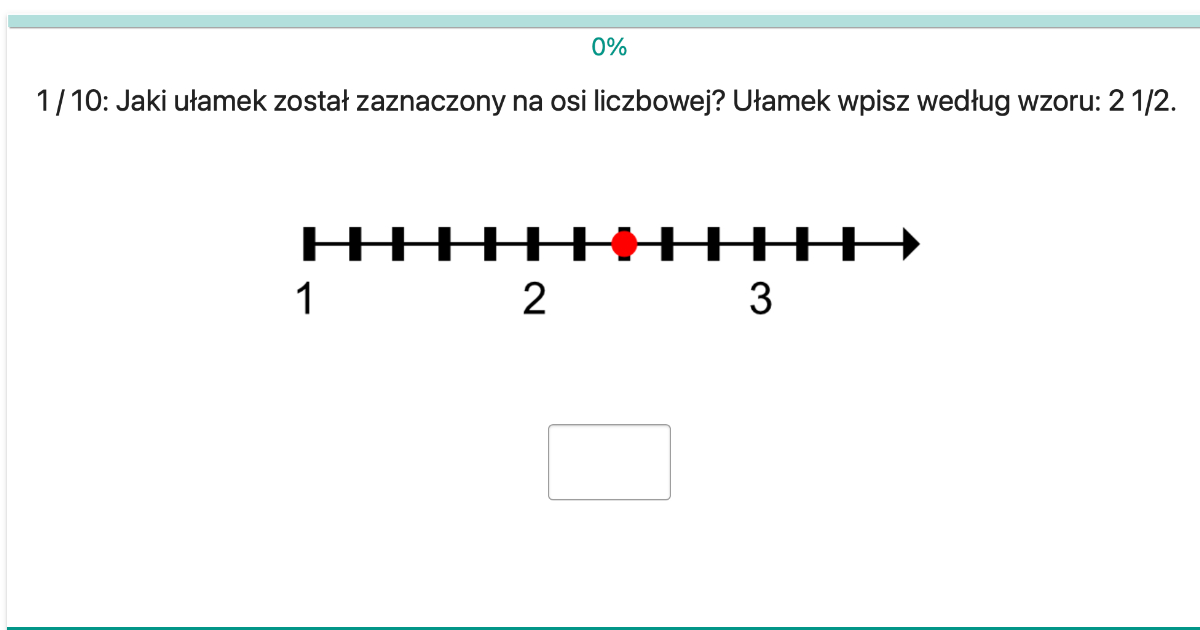
Ułamki Na Osi Liczbowej Klasa 4 Karta Pracy

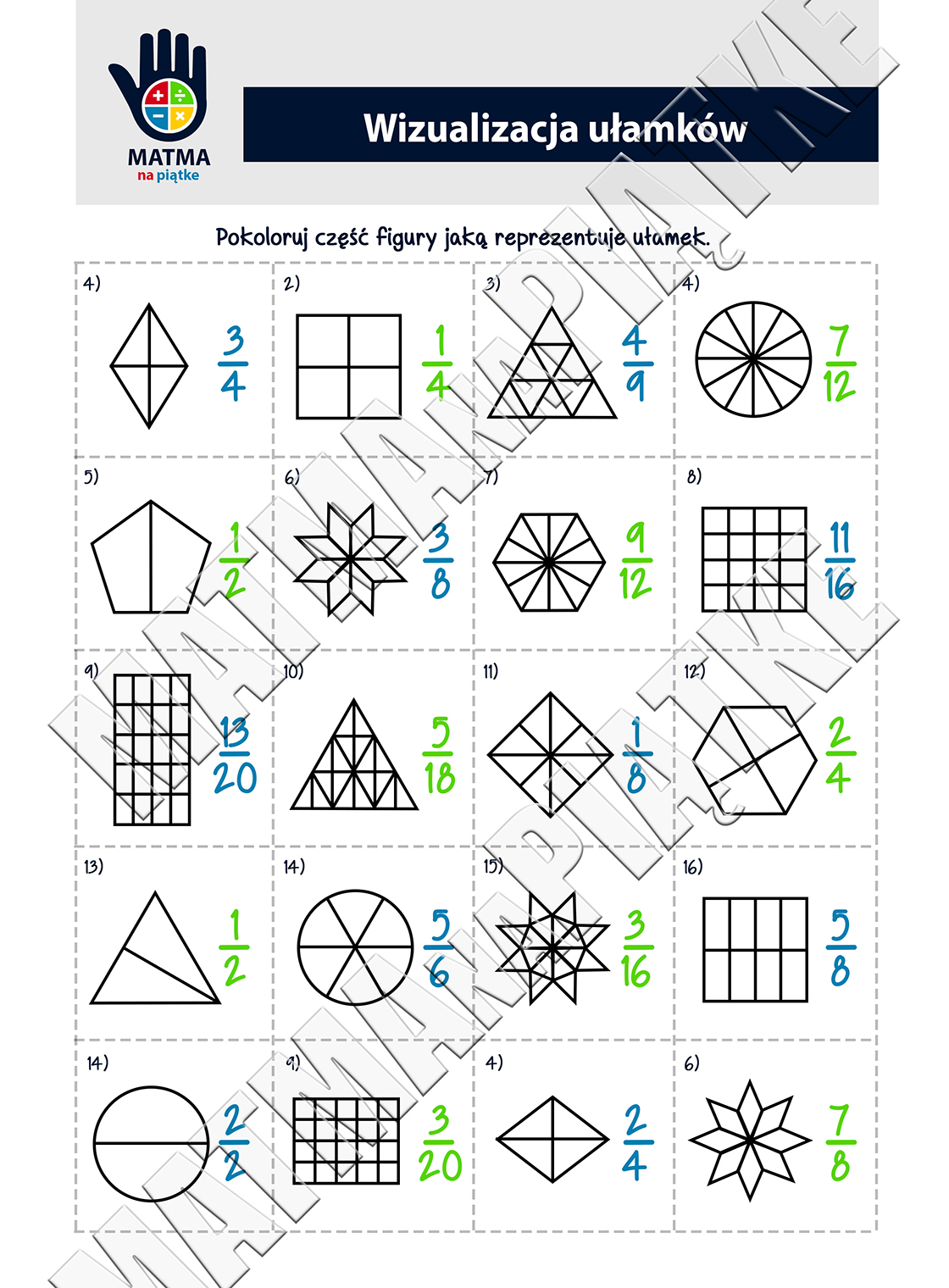
Ułamki to nie tylko abstrakcyjne liczby, ale także elementy, które możemy umieścić na osi liczbowej. Wizualizacja ułamków na osi liczbowej w klasie 4. pomaga uczniom zrozumieć ich wartość, kolejność i relacje pomiędzy nimi. Jest to fundament do opanowania bardziej zaawansowanych operacji matematycznych.

Czym jest ułamek na osi liczbowej?

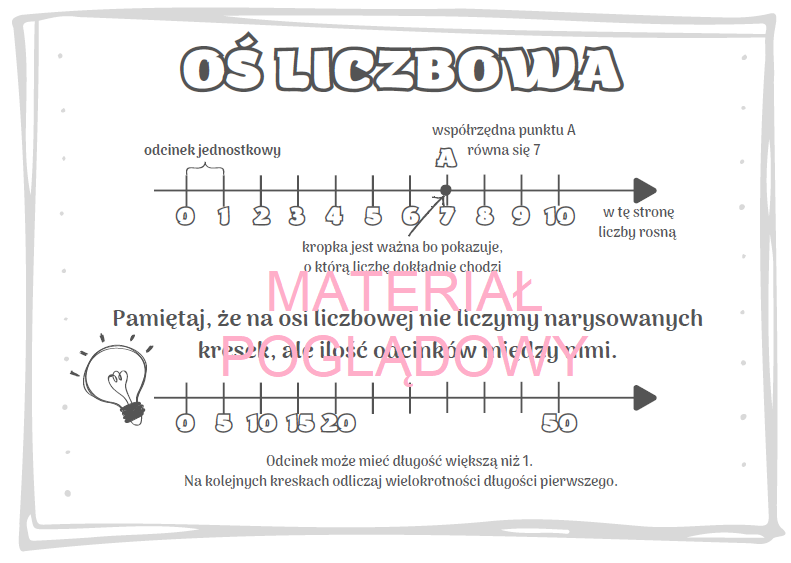
Ułamek na osi liczbowej to reprezentacja wartości ułamka na linii, gdzie odległość między kolejnymi liczbami całkowitymi (np. 0 i 1) jest podzielona na równe części, zgodnie z mianownikiem ułamka. Licznik ułamka wskazuje, ile tych części należy odmierzyć od zera, aby zaznaczyć położenie danego ułamka.

Dlaczego ułamki na osi liczbowej są ważne dla uczniów klasy 4?

Praca z ułamkami na osi liczbowej w 4. klasie ma fundamentalne znaczenie z kilku powodów:

Wizualizacja abstrakcji: Ułamki są z natury abstrakcyjne. Oś liczbowa oferuje konkretny, wizualny model, który pomaga uczniom zrozumieć, co tak naprawdę reprezentuje ułamek. Zamiast po prostu pamiętać regułki, dzieci mogą zobaczyć, jak ułamek 'wygląda' w stosunku do innych liczb.
Zrozumienie wartości ułamków: Umieszczanie ułamków na osi liczbowej pozwala uczniom zobaczyć, że niektóre ułamki są większe od innych, mimo że mogą mieć mniejsze liczniki lub większe mianowniki. To buduje intuicję dotyczącą porównywania ułamków.
Porównywanie i porządkowanie ułamków: Uczniowie mogą łatwo porównywać ułamki, obserwując ich położenie na osi liczbowej. Ułamek położony bardziej na prawo jest większy od ułamka położonego bardziej na lewo. Ułatwia to również porządkowanie ułamków od najmniejszego do największego lub odwrotnie.
Przygotowanie do dalszej nauki: Zrozumienie ułamków na osi liczbowej jest niezbędne do opanowania bardziej zaawansowanych koncepcji, takich jak dodawanie i odejmowanie ułamków, ułamki dziesiętne i procenty. Jest to solidna podstawa do dalszej nauki matematyki.

"Dzieci uczą się efektywniej, gdy pojęcia abstrakcyjne są prezentowane w sposób konkretny i wizualny" – podkreśla prof. Anna Kowalska, specjalistka w dziedzinie dydaktyki matematyki.

Jak praca z ułamkami na osi liczbowej wpływa na uczniów?

Regularna praca z kartami pracy, na których uczniowie umieszczają ułamki na osi liczbowej, przynosi wymierne korzyści:

Poprawa umiejętności wizualizacyjnych: Uczniowie rozwijają umiejętność przekształcania abstrakcyjnych pojęć w obrazy mentalne, co jest przydatne nie tylko w matematyce, ale także w innych dziedzinach.
Wzrost pewności siebie: Kiedy uczniowie widzą, że potrafią umieszczać ułamki na osi liczbowej, rośnie ich pewność siebie w rozwiązywaniu zadań matematycznych.
Lepsze zrozumienie zależności matematycznych: Oś liczbowa pomaga uczniom zrozumieć, jak ułamki odnoszą się do liczb całkowitych i innych ułamków, budując głębsze zrozumienie zależności matematycznych.
Rozwijanie umiejętności analitycznego myślenia: Umieszczanie ułamków na osi liczbowej wymaga analizy i logicznego myślenia, co rozwija umiejętności analityczne uczniów.

Praktyczne zastosowania w szkole i życiu codziennym

Umiejętność posługiwania się ułamkami na osi liczbowej ma wiele praktycznych zastosowań zarówno w szkole, jak i w życiu codziennym:

Dzielenie pizzy: Kiedy dzielimy pizzę na 8 kawałków i bierzemy 3 z nich, to mamy 3/8 pizzy. Możemy to zwizualizować na osi liczbowej, aby lepiej zrozumieć, ile pizzy zostało.
Odczytywanie miarki: Kiedy mierzymy długość przedmiotu za pomocą miarki, często musimy odczytać ułamki cala lub centymetra. Zrozumienie ułamków na osi liczbowej pomaga nam dokładnie odczytać te wartości.
Planowanie czasu: Jeśli mamy zaplanowane 30 minut na odrobienie pracy domowej, a już poświęciliśmy 1/2 tego czasu, możemy to zwizualizować na osi liczbowej, aby zobaczyć, ile czasu nam jeszcze zostało.
Gotowanie: Przepisy często wymagają użycia ułamków składników. Zrozumienie ułamków na osi liczbowej pomaga nam odmierzyć odpowiednie ilości składników.

Przykładowe zadania na kartach pracy

Typowe zadania na kartach pracy z ułamkami na osi liczbowej w klasie 4. obejmują:

Zaznaczanie danego ułamka na osi liczbowej.
Określanie, jaki ułamek odpowiada zaznaczonemu punktowi na osi liczbowej.
Porównywanie dwóch ułamków poprzez umieszczenie ich na osi liczbowej.
Uzupełnianie brakujących ułamków na osi liczbowej.
Rozwiązywanie prostych zadań tekstowych z użyciem ułamków na osi liczbowej.

Podsumowanie

Praca z ułamkami na osi liczbowej w klasie 4. jest kluczowa dla zrozumienia i opanowania tego ważnego zagadnienia matematycznego. Wizualizacja ułamków na osi liczbowej pomaga uczniom zrozumieć ich wartość, kolejność i relacje pomiędzy nimi. Regularne ćwiczenia z kartami pracy, na których uczniowie umieszczają ułamki na osi liczbowej, przynoszą wymierne korzyści, takie jak poprawa umiejętności wizualizacyjnych, wzrost pewności siebie i lepsze zrozumienie zależności matematycznych. To solidna podstawa do dalszej nauki matematyki i wykorzystywania wiedzy w życiu codziennym.