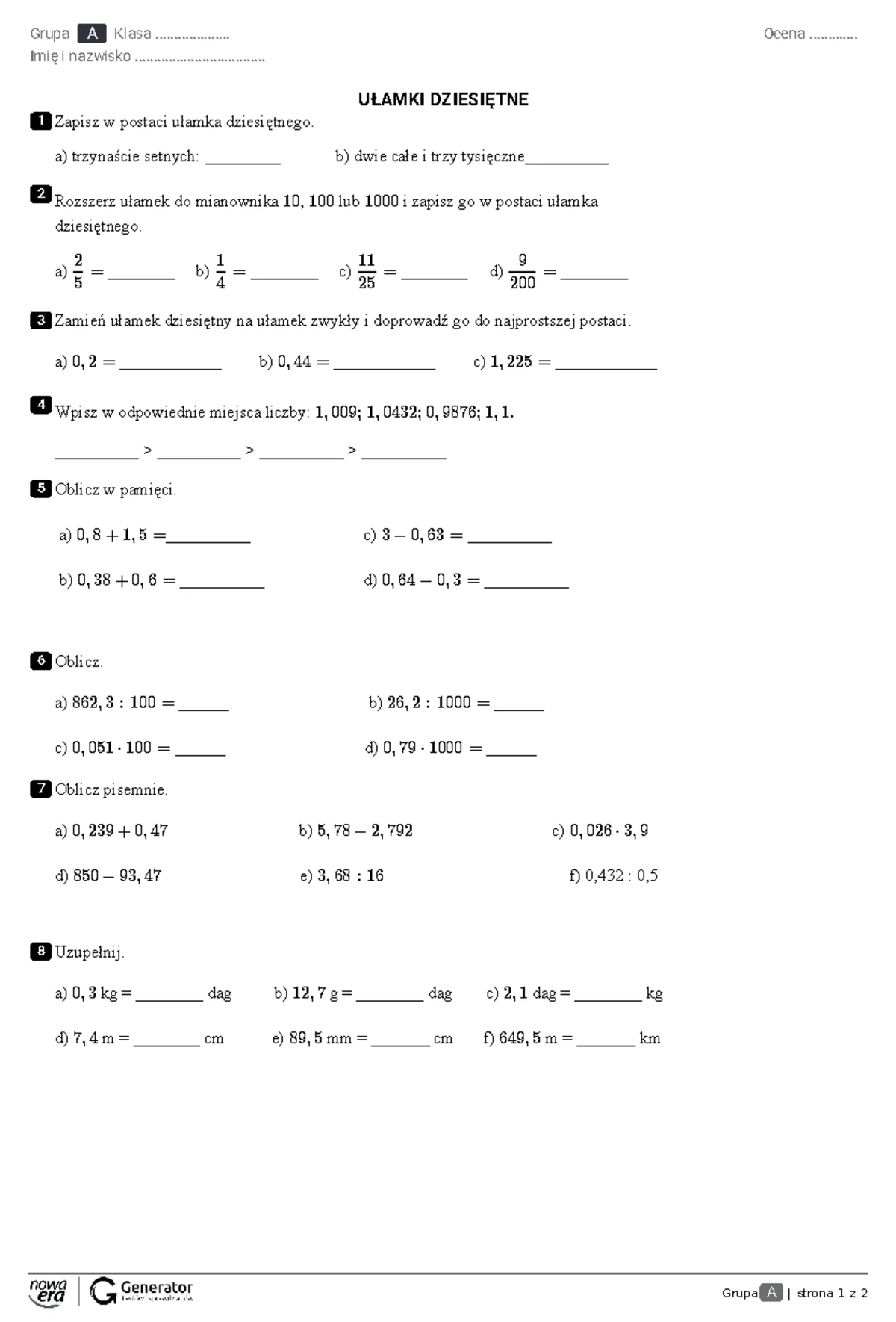
Ułamki Dziesiętne Klasa 5 Sprawdzian Matematyka

Witajcie w świecie ułamków dziesiętnych! To świetny temat, który pomoże Wam lepiej rozumieć liczby. W 5. klasie matematyki czeka Was sprawdzian z tego zagadnienia, więc postarajmy się wszystko dokładnie wyjaśnić.
Co to jest ułamek dziesiętny?
Ułamek dziesiętny to sposób zapisywania ułamków zwykłych, których mianownik (dolna część ułamka) to 10, 100, 1000 i tak dalej (czyli potęgi liczby 10). Zamiast pisać kreskę ułamkową, używamy przecinka. To wszystko!
Na przykład:
- Ułamek zwykły $\frac{3}{10}$ zapisujemy jako 0,3.
- Ułamek zwykły $\frac{7}{100}$ zapisujemy jako 0,07.
- Ułamek zwykły $\frac{15}{1000}$ zapisujemy jako 0,015.
Jak czytać ułamki dziesiętne?
Czytanie ułamków dziesiętnych jest bardzo ważne. Liczba po przecinku mówi nam, jaki to jest ułamek:
- 0,3 czytamy jako "trzy dziesiąte".
- 0,07 czytamy jako "siedem setnych".
- 0,015 czytamy jako "piętnaście tysięcznych".
Zauważcie, że liczba cyfr po przecinku odpowiada liczbie zer w mianowniku ułamka zwykłego. Jedna cyfra po przecinku to dziesiąte, dwie cyfry to setne, trzy cyfry to tysięczne, i tak dalej.
Ułamki dziesiętne a liczby całkowite
Ułamki dziesiętne mogą też mieć część całkowitą. Część całkowita to liczby przed przecinkiem. Na przykład:
- 2,5 czytamy jako "dwa i pięć dziesiątych".
- 1,25 czytamy jako "jeden i dwadzieścia pięć setnych".
- 10,009 czytamy jako "dziesięć i dziewięć tysięcznych".
Zamiana ułamków zwykłych na dziesiętne i odwrotnie
Czasem trzeba zamienić ułamek zwykły na dziesiętny lub odwrotnie.
Zwykły na dziesiętny:
- Sprawdź, czy mianownik to potęga liczby 10.
- Jeśli nie, spróbuj go taką liczbą zrobić (np. przez mnożenie). Pamiętaj, że to samo musisz zrobić z licznikiem!
- Jeśli mianownik jest 10, 100, 1000... to łatwo. Liczbę zer w mianowniku mówią Ci, ile cyfr ma być po przecinku.
Przykład: $\frac{1}{2}$. Mianownik to 2. Chcemy 10. Mnożymy przez 5: $\frac{1 \times 5}{2 \times 5} = \frac{5}{10}$. Teraz łatwo zamienić na 0,5.
Dziesiętny na zwykły:
- Policz, ile cyfr jest po przecinku.
- Tyle zer będzie w mianowniku (zawsze zaczynasz od 1).
- Liczby po przecinku to Twój licznik.
Przykład: 0,75. Są dwie cyfry po przecinku. Mianownik to 100. Licznik to 75. Czyli $\frac{75}{100}$.
Pamiętajcie, że ułamki dziesiętne to po prostu inny sposób na zapisywanie ułamków zwykłych. Ćwiczcie zamianę i czytanie, a sprawdzian z matematyki będzie dla Was bułką z masłem!