Twierdzenie O Dwusiecznej Kąta W Trójkącie

Zapraszam do zapoznania się z ciekawym zagadnieniem geometrii, mianowicie z twierdzeniem o dwusiecznej kąta w trójkącie. Jest to przydatne narzędzie, które ułatwia rozwiązywanie wielu problemów geometrycznych. Pozwoli nam zrozumieć zależności między bokami trójkąta a jego dwusieczną.
Czym jest dwusieczna kąta? Najprościej mówiąc, to prosta wychodząca z wierzchołka kąta i dzieląca ten kąt na dwie równe części. Wyobraź sobie, że masz kąt narysowany na kartce. Jeśli przetniesz go prostą, tak że powstają dwa identyczne mniejsze kąty, to ta prosta jest właśnie dwusieczną.
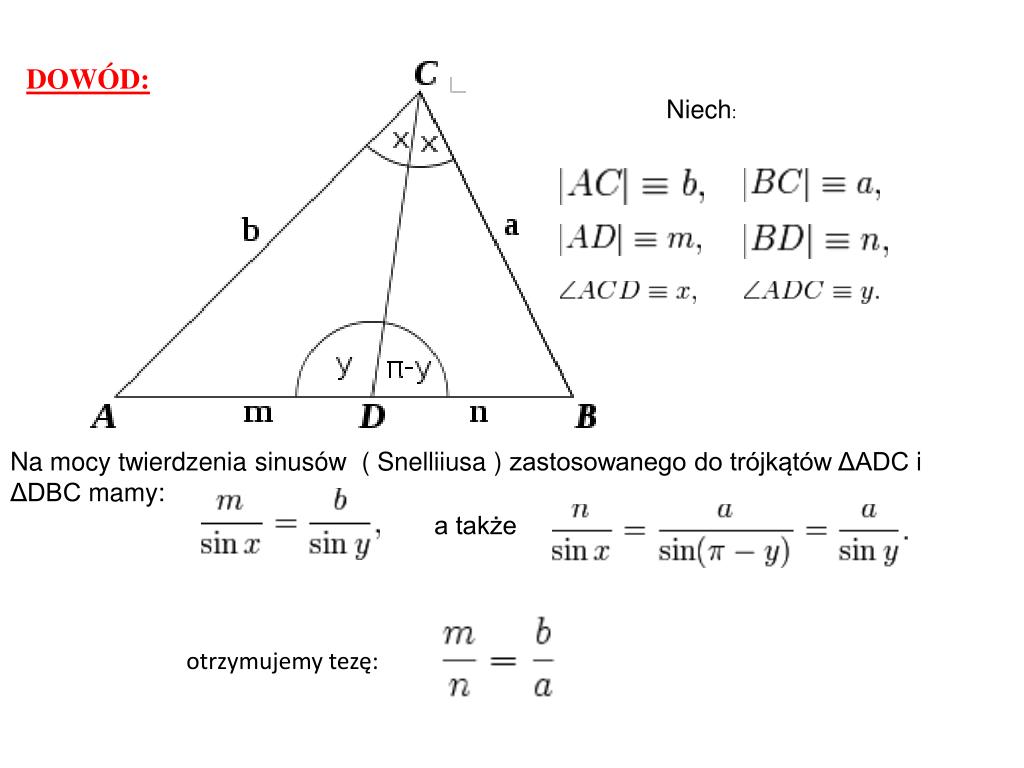
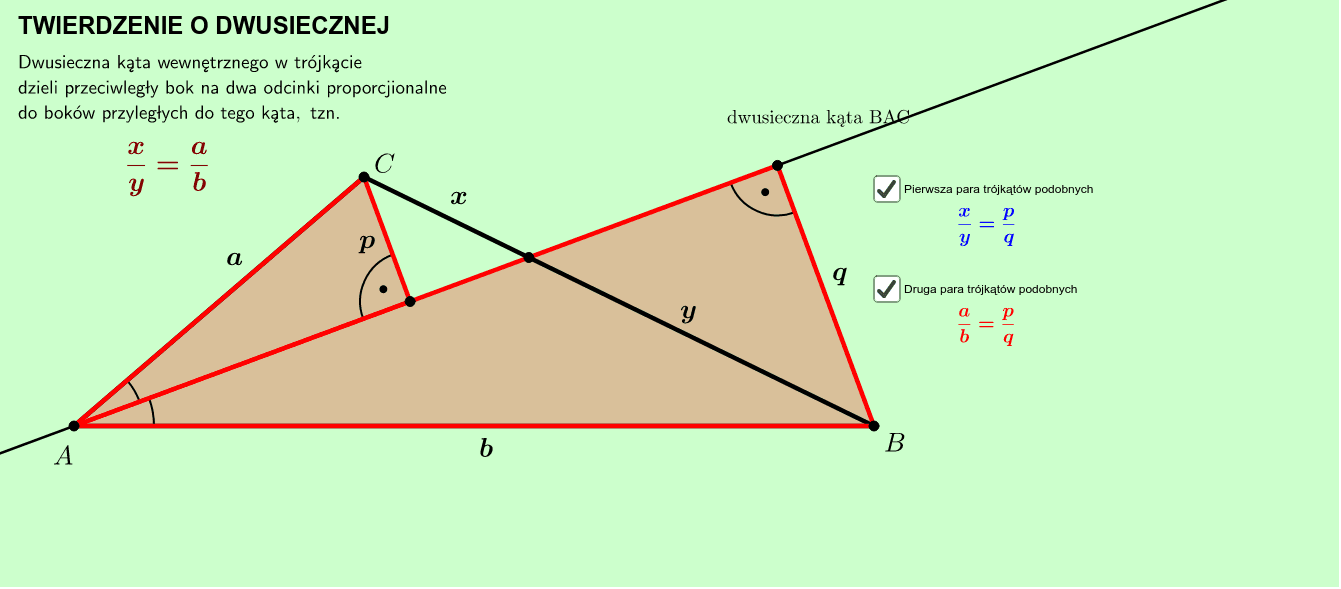
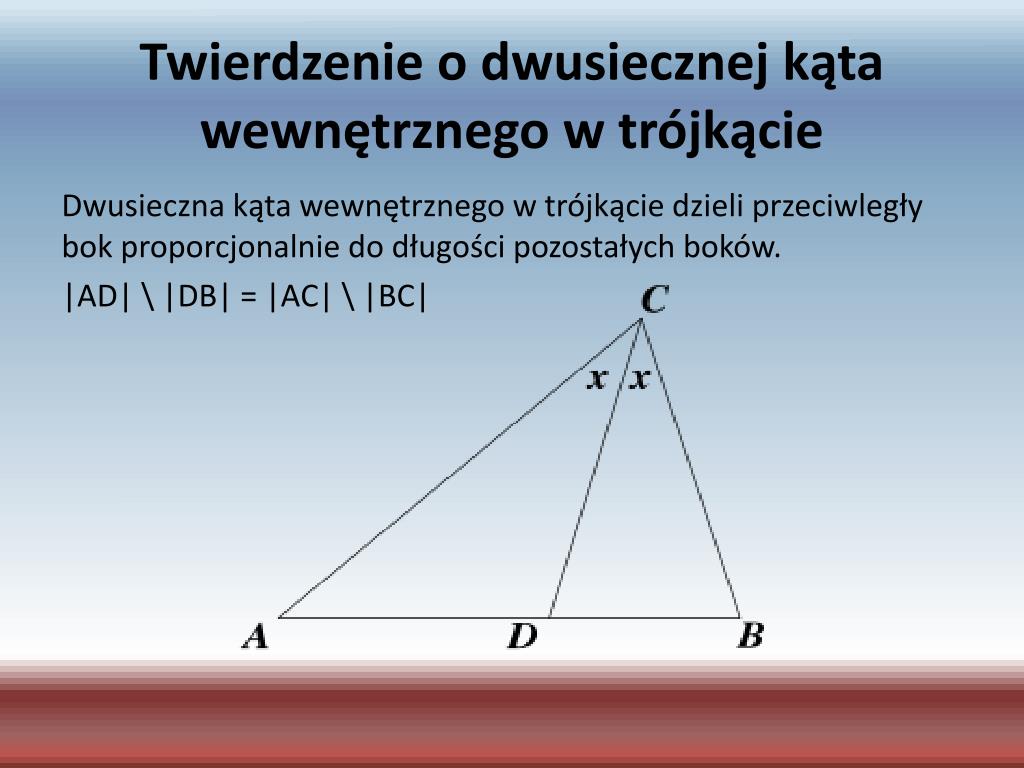
Teraz przejdźmy do samego twierdzenia. Mówi ono, że w dowolnym trójkącie, dwusieczna kąta wewnętrznego dzieli bok przeciwległy temu kątowi w stosunku długości pozostałych dwóch boków. Spróbujmy to zrozumieć na przykładzie trójkąta ABC.
Wyobraź sobie trójkąt ABC. Z wierzchołka A prowadzimy dwusieczną kąta BAC. Niech ta dwusieczna przetnie bok BC w punkcie D. Wtedy, zgodnie z twierdzeniem, stosunek długości odcinka BD do długości odcinka DC jest równy stosunkowi długości boku AB do długości boku AC. Możemy to zapisać wzorem: |BD| / |DC| = |AB| / |AC|.
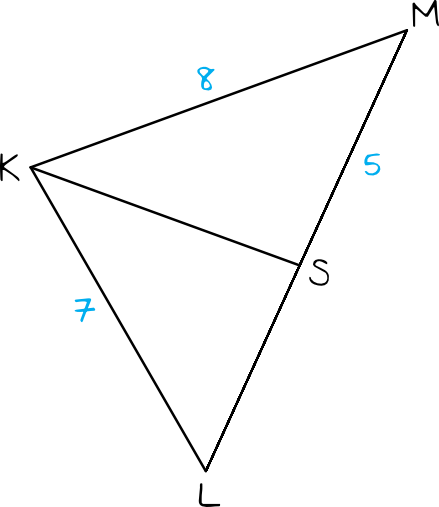
Spróbujmy rozwiązać prosty przykład. Załóżmy, że mamy trójkąt ABC, w którym |AB| = 6 cm, |AC| = 8 cm, a |BC| = 7 cm. Chcemy znaleźć długości odcinków BD i DC, powstałych przez przecięcie boku BC dwusieczną kąta BAC w punkcie D. Z twierdzenia o dwusiecznej wiemy, że |BD| / |DC| = 6/8 = 3/4. Ponadto wiemy, że |BD| + |DC| = 7 cm.
Możemy zapisać |BD| = 3x i |DC| = 4x. Stąd 3x + 4x = 7. To daje nam 7x = 7, więc x = 1. Zatem |BD| = 3 * 1 = 3 cm, a |DC| = 4 * 1 = 4 cm. W ten sposób, wykorzystując twierdzenie o dwusiecznej, znaleźliśmy długości odcinków BD i DC.
Gdzie możemy wykorzystać to twierdzenie? Poza zadaniami z geometrii, znajduje ono zastosowanie w architekturze, konstrukcji mostów i innych dziedzinach inżynierii, gdzie precyzyjne obliczenia kątów i proporcji są kluczowe. Pozwala na dokładne planowanie i realizację projektów.
Podsumowując, twierdzenie o dwusiecznej kąta w trójkącie jest bardzo przydatnym narzędziem w geometrii. Dzięki niemu możemy obliczać długości odcinków, na jakie dwusieczna dzieli bok trójkąta. Zachęcam do dalszego zgłębiania wiedzy z geometrii i wykorzystywania tego twierdzenia w praktyce.