Sprawdzian Z Matematyki Klasa 6 Pola Figur Płaskich

Nadszedł czas na jedno z bardziej wymagających, ale i kluczowych zagadnień w nauce matematyki w szóstej klasie – pola figur płaskich. To nie tylko zestaw wzorów do zapamiętania, ale przede wszystkim narzędzie pozwalające zrozumieć i opisać otaczającą nas przestrzeń. Zrozumienie, jak obliczyć powierzchnię prostokąta, trójkąta czy koła, otwiera drzwi do rozwiązywania wielu praktycznych problemów, od planowania remontu po szacowanie ilości materiałów.

Ten sprawdzian będzie doskonałą okazją, aby sprawdzić swoją wiedzę i umiejętności w tym zakresie. Skupimy się na najważniejszych figurach, ich właściwościach i metodach obliczania ich pól. Pamiętajmy, że matematyka to logiczne myślenie, a każdy wzór ma swoje uzasadnienie, które warto próbować zrozumieć.

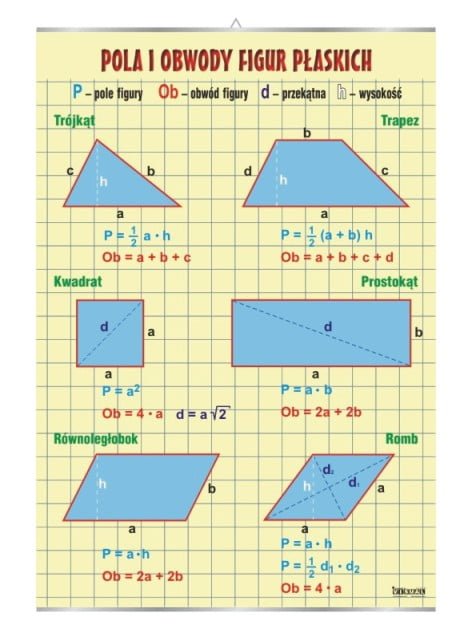
Kluczowe figury i ich pola

W sixth grade, uczniowie skupiają się na kilku podstawowych figurach geometrycznych, które stanowią fundament do dalszego zgłębiania wiedzy o polach. Każda z nich ma swoje unikalne cechy, które decydują o sposobie obliczania jej powierzchni.

Prostokąt i kwadrat

Najprostszymi figurami są prostokąt i kwadrat. Prostokąt charakteryzuje się tym, że ma cztery boki, a przeciwległe boki są równej długości. Dodatkowo, wszystkie jego kąty są kątami prostymi (90 stopni).

Obliczenie pola prostokąta jest intuicyjne. Wystarczy pomnożyć długość jednego boku przez długość boku do niego przyległego. Często używamy terminów długość (a) i szerokość (b).

Wzór na pole prostokąta: P = a * b

Kwadrat to szczególny przypadek prostokąta, gdzie wszystkie boki są równej długości. Jeśli bok kwadratu ma długość 'a', to jego pole obliczymy mnożąc długość boku przez siebie.

Wzór na pole kwadratu: P = a * a = a²

Przykład z życia: Wyobraźmy sobie, że chcemy położyć płytki na podłodze w prostokątnym pokoju o wymiarach 4 metry na 5 metrów. Aby obliczyć, ile płytek potrzebujemy (zakładając, że jedna płytka ma pole 1 m²), musimy obliczyć pole podłogi: P = 4 m * 5 m = 20 m². Jeśli mamy kwadratowy ogródek o boku 10 metrów i chcemy obsiać go trawą, potrzebujemy obliczyć jego pole: P = 10 m * 10 m = 100 m².

Trójkąt

Trójkąt to figura geometryczna o trzech bokach i trzech kątach. Tutaj obliczenie pola wymaga nieco innego podejścia, ponieważ trójkąty mogą przyjmować różne kształty – mogą być prostokątne, równoboczne, równoramienne czy różnoboczne.

Kluczowymi pojęciami przy obliczaniu pola trójkąta są podstawa i wysokość opuszczona na tę podstawę. Podstawa to dowolny bok trójkąta, a wysokość to odcinek prostopadły do tej podstawy (lub jej przedłużenia), łączący ją z przeciwległym wierzchołkiem.

Wzór na pole trójkąta: P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to długość wysokości opuszczonej na tę podstawę.

Dlaczego dzielimy przez 2? Można to sobie wyobrazić, że każdy trójkąt można wpisać w prostokąt (lub równoległobok) w taki sposób, że zajmuje dokładnie połowę jego powierzchni. Lub, że dwa identyczne trójkąty tworzą równoległobok, którego pole jest równe iloczynowi podstawy i wysokości, więc pole jednego trójkąta to połowa tej wartości.

Przykład z życia: Projektujemy dach domu. Jedna z jego ścian ma kształt trójkąta. Podstawa tego trójkąta wynosi 12 metrów, a wysokość dachu, mierzona od podstawy do najwyższego punktu, wynosi 5 metrów. Aby oszacować powierzchnię, którą trzeba pokryć dachówką, obliczamy pole: P = (12 m * 5 m) / 2 = 60 m² / 2 = 30 m².

Równoległobok

Równoległobok to figura o czterech bokach, w której przeciwległe boki są równoległe i równej długości. W przeciwieństwie do prostokąta, kąty równoległoboku nie muszą być proste.

Podobnie jak w przypadku trójkąta, do obliczenia pola równoległoboku potrzebujemy znać długość podstawy i odpowiadającej jej wysokości. Wysokość to odcinek prostopadły do podstawy (lub jej przedłużenia) i łączący ją z przeciwległym bokiem.

Wzór na pole równoległoboku: P = a * h, gdzie 'a' to długość podstawy, a 'h' to długość wysokości opuszczonej na tę podstawę.

Można sobie wyobrazić, że równoległobok można "przekształcić" w prostokąt o tej samej podstawie i wysokości, przez "ścięcie" jednego z boków i "dołożenie" go do drugiej strony. Dlatego wzór jest taki sam jak dla prostokąta.

Przykład z życia: Jesteśmy na etapie projektowania mebli. Chcemy stworzyć stolik kawowy o blacie w kształcie równoległoboku. Jedna z dłuższych krawędzi (podstawa) ma 1 metr długości, a odległość między tymi równoległymi bokami (wysokość) wynosi 0.6 metra. Pole blatu, a tym samym ilość potrzebnego materiału (np. drewna) obliczymy jako: P = 1 m * 0.6 m = 0.6 m².

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami (oznaczamy je jako 'a' i 'b'). Pozostałe dwa boki nazywamy ramionami.

Do obliczenia pola trapezu potrzebujemy znać długości obu podstaw oraz wysokość trapezu. Wysokość to odległość między podstawami, mierzona wzdłuż odcinka prostopadłego do obu podstaw.

Wzór na pole trapezu: P = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość trapezu.

Wzór ten można zinterpretować jako średnią arytmetyczną długości podstaw pomnożoną przez wysokość. Można też myśleć o trapezie jako o dwóch trójkątach i prostokącie (w przypadku trapezu prostokątnego) lub jako o figurze, która zajmuje połowę powierzchni prostokąta o boku równym sumie podstaw i wysokości.

Przykład z życia: Planujemy utworzenie ogrodu warzywnego. Jedna z jego części ma kształt trapezu, gdzie jedna podstawa ma 8 metrów, druga 6 metrów, a odległość między nimi (wysokość) wynosi 3 metry. Aby obliczyć powierzchnię tej części ogrodu: P = ((8 m + 6 m) * 3 m) / 2 = (14 m * 3 m) / 2 = 42 m² / 2 = 21 m².

Koło

Koło to figura geometryczna będąca zbiorem wszystkich punktów płaszczyzny, które leżą w równej odległości od ustalonego punktu, zwanego środkiem koła. Ta odległość to promień (oznaczany jako 'r').

Obliczenie pola koła opiera się na stałej matematycznej zwanej pi (π), której przybliżona wartość wynosi 3.14.

Wzór na pole koła: P = π * r², gdzie 'r' to promień koła.

Wartość π jest liczbą niewymierną, co oznacza, że jej rozwinięcie dziesiętne jest nieskończone i nieokresowe. W obliczeniach szkolnych często używamy przybliżonej wartości 3.14.

Przykład z życia: Chcemy zbudować okrągłą studnię. Jej promień wynosi 2 metry. Aby obliczyć, ile betonu potrzeba na jej dno, obliczamy pole: P = π * (2 m)² = π * 4 m² ≈ 3.14 * 4 m² = 12.56 m².

Praktyczne zastosowania i znaczenie

Nauka obliczania pól figur płaskich to nie tylko ćwiczenie na sprawdzianie, ale przede wszystkim rozwijanie umiejętności, które mają realne zastosowanie w codziennym życiu. Architekci, inżynierowie, projektanci wnętrz, a nawet ogrodnicy – wszyscy oni na co dzień korzystają z tych samych zasad.

Remonty i dekoracje: Gdy planujemy malowanie ścian, musimy znać ich powierzchnię. Jeśli ściany są prostokątne, obliczenie jest proste. Czasem jednak pojawiają się elementy o bardziej skomplikowanych kształtach, np. wnęki czy łuki, które mogą wymagać zastosowania wzorów na pola trójkątów czy trapezów.

Budownictwo i przemysł: W przemyśle potrzeba obliczania powierzchni jest wszechobecna. Od produkcji materiałów budowlanych, przez projektowanie elementów maszyn, aż po tworzenie opakowań – wszędzie tam znajomość pól jest kluczowa. Na przykład, aby obliczyć ilość blachy potrzebną do wykonania okrągłej pokrywy, musimy znać pole koła.

Gastronomia: Nawet w kuchni możemy natknąć się na potrzebę obliczania pól. Krojenie pizzy na równe kawałki (trójkąty) czy dzielenie tortu wymaga zrozumienia proporcji i kształtów.

Rolnictwo i ogrodnictwo: Planowanie rozmieszczenia upraw, szacowanie ilości nawozu czy nasion, a nawet projektowanie altan i ścieżek w ogrodzie – to wszystko wymaga obliczeń związanych z powierzchnią.

Sztuka i projektowanie: Artyści i projektanci często pracują z kształtami i powierzchniami. Malując obrazy, tworząc grafiki, czy projektując tkaniny, świadomie lub intuicyjnie operują pojęciami pola i kształtu.

Przygotowanie do sprawdzianu

Aby dobrze przygotować się do sprawdzianu z pól figur płaskich, należy:

• Dokładnie zapamiętać wzory: Poświęć czas na nauczenie się każdego wzoru. Zapisz je, powtarzaj, wyjaśniaj je sobie nawzajem.
• Ćwiczyć, ćwiczyć, ćwiczyć: Rozwiąż jak najwięcej zadań. Zaczynaj od prostych przykładów, stopniowo przechodząc do tych bardziej złożonych.
• Rozumieć pojęcia: Nie ucz się na pamięć, staraj się zrozumieć, dlaczego dany wzór działa. Wyobrażaj sobie figury, rysuj je.
• Analizować treści zadań: Zanim zaczniesz liczyć, dokładnie przeczytaj zadanie. Zastanów się, jaka figura jest opisana, jakie dane są podane i czego należy obliczyć.
• Sprawdzać jednostki: Pamiętaj o poprawnym zapisywaniu jednostek. Jeśli wymiary podane są w centymetrach, pole będzie w centymetrach kwadratowych.

Pamiętajmy, że każdy sprawdzian to szansa na naukę i rozwój. Nie należy się go bać, ale potraktować jako wyzwanie. Skupienie, systematyczna praca i próba zrozumienia materiału to klucz do sukcesu. Powodzenia!