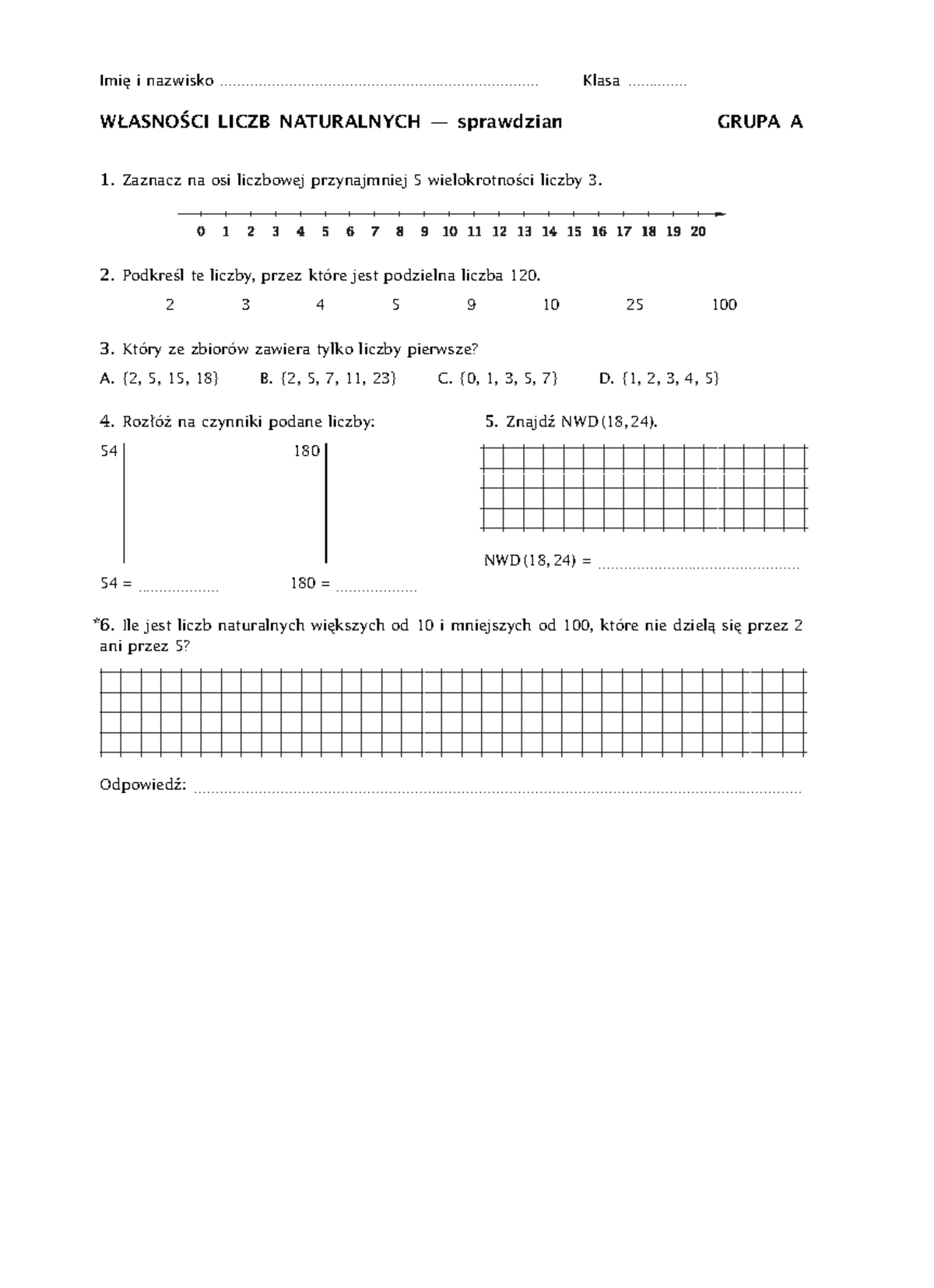
Sprawdzian Własności Liczb Naturalnych Klasa 5

Sprawdzian Własności Liczb Naturalnych Klasa 5. Co to takiego? Mówiąc najprościej, to test, który sprawdza, czy rozumiesz, jakie cechy mają liczby naturalne. Liczby naturalne to po prostu liczby, którymi liczymy: 1, 2, 3, 4, i tak dalej. Nie ma tu ułamków, liczb ujemnych, ani zera (chociaż w niektórych definicjach zero się zalicza!). Sprawdzian ten zazwyczaj skupia się na podzielności, resztach z dzielenia i rozpoznawaniu liczb parzystych i nieparzystych.

Jak to działa? Wyobraź sobie, że masz paczkę ciasteczek. Powiedzmy, że jest ich 12. Sprawdzian z własności liczb może zapytać, czy 12 ciasteczek da się sprawiedliwie podzielić między 2 osoby. Da się! Każda osoba dostanie 6 ciasteczek. To znaczy, że 12 jest podzielne przez 2. Albo, czy 12 ciasteczek da się podzielić po równo między 5 osób? Nie da się! Każda osoba dostanie 2 ciasteczka, ale zostaną 2 ciasteczka, których nie da się już podzielić. Mówimy wtedy, że reszta z dzielenia 12 przez 5 wynosi 2. Podsumowując:

• Podzielność: Liczba jest podzielna przez inną liczbę, jeśli po podzieleniu nie ma reszty. Na przykład, 10 jest podzielne przez 2 i 5.
• Parzyste i Nieparzyste: Liczby parzyste to te, które dzielą się przez 2 bez reszty (2, 4, 6, 8, ...). Liczby nieparzyste zostawiają resztę 1, gdy dzielimy je przez 2 (1, 3, 5, 7, ...).
• Reszta z Dzielenia: To to, co zostaje, gdy nie da się już podzielić liczby całkowicie. Na przykład, reszta z dzielenia 7 przez 3 to 1 (bo 7 = 3 x 2 + 1).

Często na sprawdzianie pojawiają się pytania o to, czy liczba jest podzielna przez 2, 3, 5, czy 10. Istnieją proste zasady podzielności, które ułatwiają odpowiedź na to pytanie, bez wykonywania dzielenia pisemnego. Na przykład:

• Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6, 8).
• Podzielność przez 5: Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5.
• Podzielność przez 10: Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0.
• Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. Na przykład, liczba 123 jest podzielna przez 3, ponieważ 1 + 2 + 3 = 6, a 6 jest podzielne przez 3.

Dlaczego to jest ważne? Rozumienie własności liczb naturalnych jest jak budowanie solidnego fundamentu pod cały świat matematyki! Pomaga w prostych obliczeniach, takich jak dzielenie się jedzeniem z przyjaciółmi, planowanie wydatków, czy obliczanie, ile czasu zajmie ci pokonanie pewnej trasy. Ale przede wszystkim, zrozumienie tych zasad pomaga w rozwiązywaniu bardziej skomplikowanych problemów w przyszłości, np. w algebrze, geometrii, a nawet w programowaniu komputerów. Znajomość podzielności ułatwia upraszczanie ułamków i rozwiązywanie równań. Im lepiej zrozumiesz własności liczb teraz, tym łatwiej będzie ci w przyszłości z matematyką!