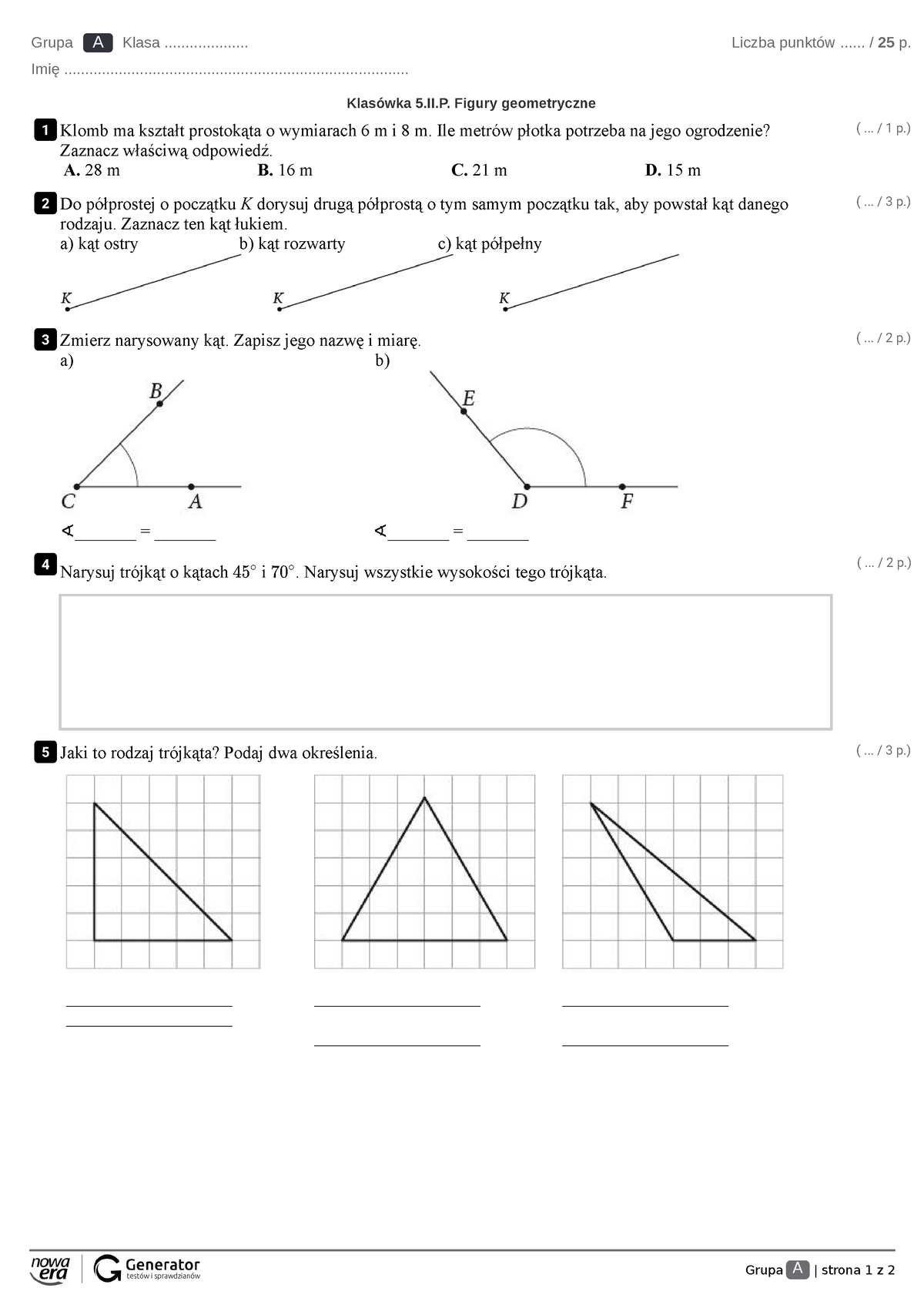
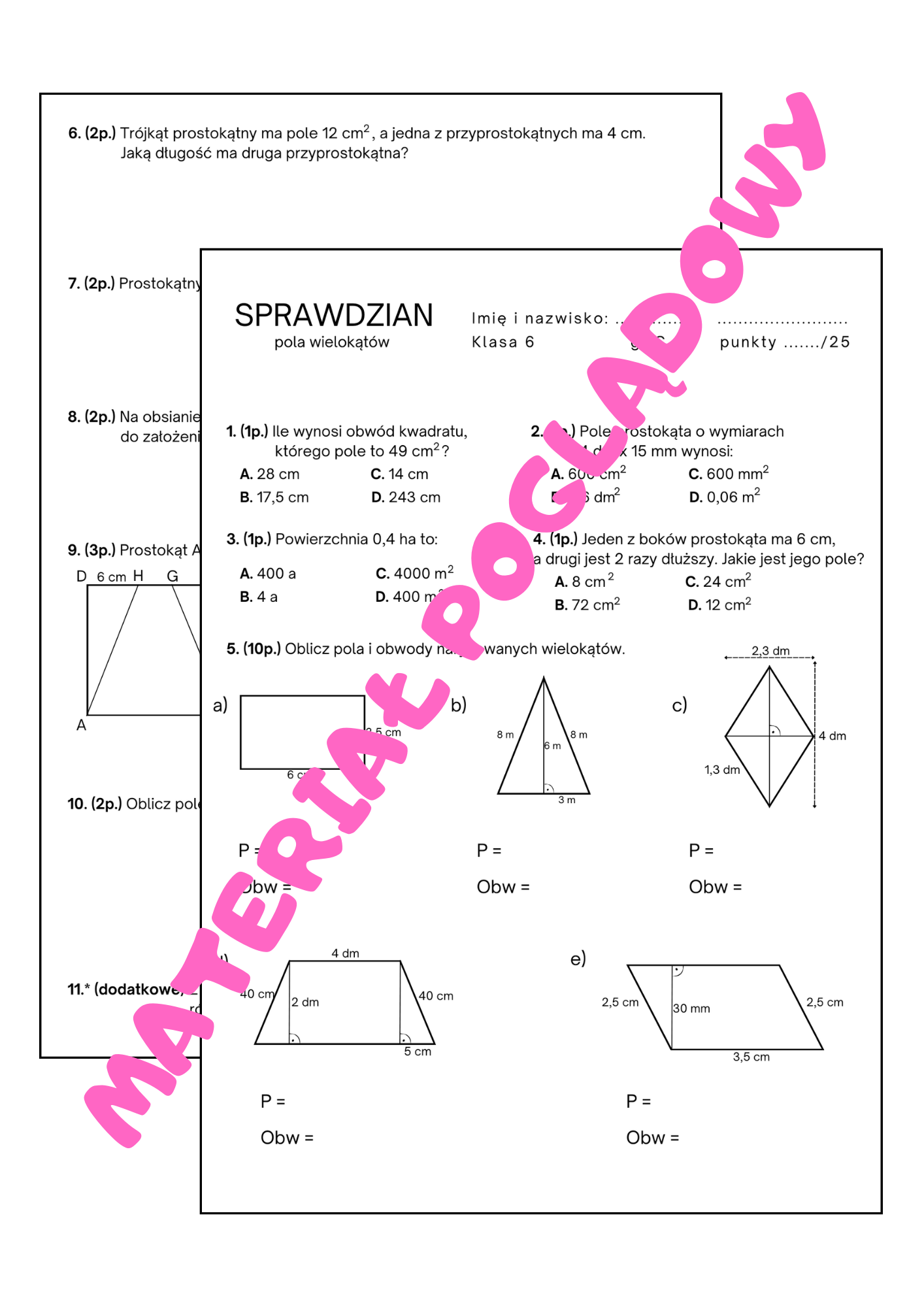
Sprawdzian Pole Trójkątów I Czworokątów Klasa 5

Pamiętacie to uczucie, gdy przed nami pojawia się kartkówka z matematyki, a konkretnie sprawdzian z pól figur? Szczególnie sprawdzian z

pól trójkątów i czworokątów

niepokój

Jednak zamiast poddawać się stresowi, podejdźmy do tego wyzwania z ciekawością i chęcią zrozumienia. W dzisiejszym artykule przyjrzymy się bliżej temu, czego można spodziewać się na sprawdzianie z pól figur, dlaczego jest to ważne i jak najlepiej się do niego przygotować. Chcemy, aby ten tekst był dla Was nie tylko źródłem wiedzy, ale także inspiracją i praktycznym przewodnikiem.

Dlaczego Uczymy się o Polach Figur?

Może się zastanawiacie: "Po co mi te wszystkie wzory na trójkąty i czworokąty? Czy naprawdę kiedykolwiek ich użyję?". Odpowiedź brzmi: tak! Geometria, a w niej obliczanie pól powierzchni, to nie tylko ćwiczenie umysłowe, ale także kluczowa umiejętność praktyczna. Projektowanie wnętrz, budowanie domu, szycie, a nawet układanie płytek – to wszystko wymaga zrozumienia, ile miejsca zajmują dane przedmioty lub powierzchnie.

Jak zauważają liczni pedagodzy, zrozumienie przestrzeni i jej wymiarów jest fundamentalne dla rozwoju logicznego myślenia. Kiedy dzieci uczą się obliczać pola, rozwijają swoje zdolności do:

• Rozpoznawania kształtów i ich cech.
• Wyobraźni przestrzennej – widzenia obiektów w trzech wymiarach.
• Stosowania formuł i algorytmów.
• Rozwiązywania problemów – szukania optymalnych rozwiązań.

W klasie piątej skupiamy się na dwóch głównych grupach figur: czworokątach (kwadrat, prostokąt, romb, równoległobok, trapez) i trójkątach. Każda z tych figur ma swoje specyficzne cechy, które wpływają na sposób obliczania jej pola.

Kluczowe Figury i Ich Wzory

Na sprawdzianie z pewnością pojawią się zadania wymagające obliczenia pola podstawowych figur. Warto je sobie przypomnieć i utrwalić:

Czworokąty

• Kwadrat: Wszystkie boki są równe. Pole kwadratu obliczamy mnożąc długość boku przez siebie: P = a * a (gdzie 'a' to długość boku).
• Prostokąt: Dwie pary równych boków. Pole prostokąta to iloczyn długości jego boków: P = a * b (gdzie 'a' i 'b' to długości sąsiednich boków).
• Romb: Czworokąt o wszystkich bokach równych. Jego pole obliczamy na dwa sposoby:
  • Jako połowę iloczynu długości jego przekątnych: P = (p * q) / 2 (gdzie 'p' i 'q' to długości przekątnych).
  • Jeśli znamy długość boku i wysokość opuszczoną na ten bok: P = a * h (gdzie 'a' to długość boku, a 'h' to wysokość).
• Równoległobok: Czworokąt, którego przeciwległe boki są równoległe i równe. Pole równoległoboku to iloczyn długości jego boku i wysokości opuszczonej na ten bok: P = a * h.
• Trapez: Czworokąt, który ma co najmniej jedną parę boków równoległych (nazywane podstawami). Pole trapezu obliczamy dodając długości podstaw, mnożąc sumę przez wysokość, a następnie dzieląc przez dwa: P = ((a + b) * h) / 2 (gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość).

Trójkąty

Trójkąty mogą być bardziej podchwytliwe, ale ich pole zawsze można obliczyć, znając odpowiednie wymiary. Główny wzór na pole trójkąta to:

• P = (a * h) / 2 (gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę).

Kluczowe jest tutaj zrozumienie pojęcia wysokości. Wysokość to odcinek poprowadzony z wierzchołka trójkąta, prostopadły do przeciwległego boku (lub jego przedłużenia). Niezależnie od tego, który bok wybierzemy jako podstawę, wysokość opuszczona na ten bok zawsze pozwoli nam obliczyć pole.

Co Może Znaleźć się na Sprawdzianie?

Sprawdzian z pól figur w klasie piątej zazwyczaj obejmuje:

• Obliczanie pola konkretnych figur, gdy podane są wszystkie potrzebne wymiary (np. prostokąt o bokach 5 cm i 10 cm).
• Obliczanie pola figur, gdzie trzeba najpierw wyznaczyć brakujący wymiar (np. kwadrat o obwodzie 20 cm).
• Zadania tekstowe, które wymagają zastosowania wzorów w praktycznym kontekście (np. obliczenie powierzchni działki, opakowania).
• Figury złożone – zadania, gdzie trzeba podzielić skomplikowany kształt na mniejsze, znane figury, obliczyć ich pola, a następnie je dodać lub odjąć.
• Porównywanie pól figur – określanie, która figura ma większe pole.

Jak Się Przygotować? Skuteczne Metody

Stres przed sprawdzianem jest naturalny, ale można go znacząco zredukować poprzez odpowiednie przygotowanie. Oto kilka sprawdzonych metod:

1. Zrozumienie, Nie Zapamiętywanie

Największym błędem jest próba "wkuwania" wzorów na pamięć. Zamiast tego, postarajcie się zrozumieć, skąd dany wzór się wziął. Na przykład, pole prostokąta to a*b, bo można go podzielić na 'a' rzędów po 'b' kwadracików jednostkowych. Pole rombu jako połowa iloczynu przekątnych wynika z tego, że romb można wpisać w prostokąt, którego przekątne są bokami prostokąta, a jego pole jest dwukrotnie większe.

"Uczniowie, którzy rozumieją kontekst i pochodzenie wzorów, lepiej radzą sobie z ich zastosowaniem w nowych, nieznanych sytuacjach." – to często powtarzana obserwacja przez nauczycieli matematyki.

2. Wizualizacja i Rysowanie

Rysujcie! Zawsze, gdy macie zadanie związane z geometrią, poświęćcie chwilę na narysowanie figury. Oznaczcie boki, wysokości, przekątne. Pomaga to wyobrazić sobie problem i zobaczyć, jakie dane są dostępne, a jakie trzeba wyznaczyć.

Przykładowo: Rysując równoległobok, narysujcie go, a następnie zaznaczcie wysokość opuszczoną na jeden z boków. Zobaczycie, że tworzy ona trójkąt prostokątny, co może być pomocne w dalszych obliczeniach.

3. Rozwiązywanie Różnorodnych Zadań

Kluczem do sukcesu jest praktyka. Rozwiązujcie jak najwięcej zadań z różnych źródeł: podręcznika, zeszytu ćwiczeń, dodatkowych zbiorów zadań, a nawet zadań online.

• Zadania typu "krok po kroku": Najpierw ćwiczcie proste zadania z podanymi wszystkimi danymi, potem stopniowo przechodźcie do trudniejszych, wymagających dodatkowych obliczeń lub podziału figur.
• Zadania "na odwrót": Jeśli znacie pole i jeden z wymiarów, spróbujcie obliczyć drugi wymiar.

4. Utrwalanie Wzorów

Gdy już rozumiecie wzory, warto je utrwalić. Możecie:

• Stworzyć "ściągawkę" z najważniejszymi wzorami, którą będziecie mieć pod ręką podczas nauki (nie na sprawdzianie!).
• Używać kart pracy z pustymi miejscami na wzory.
• Powtarzać je na głos.

5. Figury Złożone – Klucz do Sukcesu

Zadania z figurami złożonymi to często moment, w którym uczniowie się gubią. Jak sobie z nimi poradzić?

• Podziel na prostsze części: Zawsze starajcie się rozbić skomplikowany kształt na prostokąty, kwadraty, trójkąty.
• Zaznaczajcie podział na rysunku.
• Obliczajcie pola poszczególnych figur.
• Łączcie wyniki: Dodawajcie pola figur składowych, jeśli tworzą większą całość, lub odejmujcie, jeśli jedna figura jest "wycięta" z drugiej.

Przykład: Kształt domu (prostokąt z trójkątem na górze). Obliczamy pole prostokąta, potem pole trójkąta i sumujemy.

6. Praca z Nauczycielem i Rówieśnikami

Nie bójcie się pytać! Jeśli czegoś nie rozumiecie, zapytajcie nauczyciela. Wspólne rozwiązywanie zadań z kolegami i koleżankami również może być bardzo pomocne – często inna perspektywa pozwala dostrzec rozwiązanie.

Przykładowe Zadania ze Sprawdzianu

Abyście mieli lepsze wyobrażenie, oto kilka typów zadań, które mogą pojawić się na sprawdzianie:

1. Oblicz pole prostokąta o bokach 7 cm i 12 cm.
2. Kwadrat ma obwód 32 metry. Jakie jest jego pole?
3. Oblicz pole trapezu, którego podstawy mają długości 8 cm i 14 cm, a wysokość wynosi 5 cm.
4. Rysunek przedstawia równoległobok. Długość jednego z boków wynosi 10 cm, a odpowiadająca mu wysokość to 6 cm. Oblicz pole tego równoległoboku.
5. Oblicz pole trójkąta o podstawie 15 cm i wysokości opuszczonej na tę podstawę wynoszącej 8 cm.
6. Działka ma kształt prostokąta o wymiarach 20 m na 30 m. Oblicz jej powierzchnię.
7. Z podwórka w kształcie prostokąta o bokach 50 m i 100 m wydzielono prostokątny plac zabaw o wymiarach 20 m na 25 m. Jakie jest pole pozostałej części podwórka?

Podsumowanie

Sprawdzian z pól trójkątów i czworokątów to okazja do pokazania, czego nauczyliście się przez ostatnie tygodnie. Pamiętajcie, że opanowanie tych zagadnień wymaga czasu i praktyki. Skupcie się na zrozumieniu wzorów, wizualizacji figur i regularnym rozwiązywaniu zadań. Nie zrażajcie się trudnościami – każde rozwiązane zadanie to krok naprzód.

Z odpowiednim przygotowaniem, a przede wszystkim z pozytywnym nastawieniem, ten sprawdzian może stać się nie tylko dowodem Waszej wiedzy, ale także początkiem fascynującej podróży po świecie geometrii. Powodzenia!