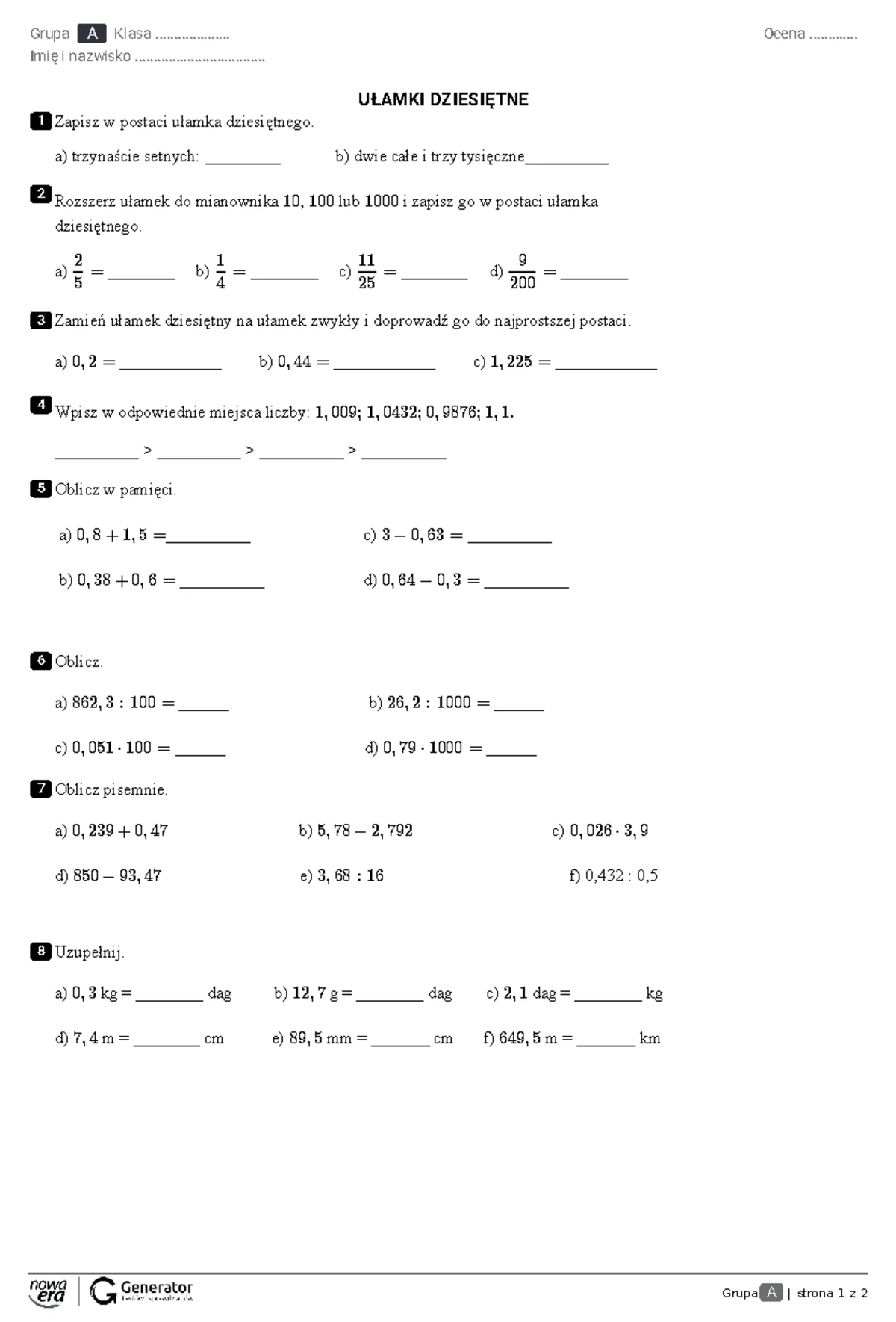
Sprawdzian Matematyka Klasa 5 Liczby Dziesiętne

Liczby dziesiętne to sposób zapisu liczb, który wykorzystuje przecinek do oddzielenia części całkowitej od części ułamkowej. Każda cyfra po przecinku ma swoje określone miejsce, reprezentujące potęgi dziesiątki (np. dziesiąte, setne, tysięczne).

Zrozumienie liczb dziesiętnych jest kluczowe w matematyce klasy 5. Zacznijmy od podstaw.

Krok 1: Zrozumienie miejsca cyfr

W liczbach dziesiętnych każda cyfra ma swoją wartość zależną od pozycji. Po lewej stronie przecinka mamy część całkowitą (jedności, dziesiątki, setki itd.). Po prawej stronie przecinka mamy część ułamkową:

• Pierwsza cyfra po przecinku to dziesiąte (czyli 1/10).
• Druga cyfra po przecinku to setne (czyli 1/100).
• Trzecia cyfra po przecinku to tysięczne (czyli 1/1000).

Przykład: W liczbie 12,345:

• 1 to cyfra dziesiątek.
• 2 to cyfra jedności.
• 3 to cyfra dziesiątych.
• 4 to cyfra setnych.
• 5 to cyfra tysięcznych.

Krok 2: Zamiana ułamków zwykłych na dziesiętne

Możemy zamienić ułamek zwykły na dziesiętny, dzieląc licznik przez mianownik. Ważne, aby mianownik był potęgą dziesiątki (10, 100, 1000...).

Przykład:

• Ułamek 1/2: 1 dzielone przez 2 to 0,5.
• Ułamek 3/4: 3 dzielone przez 4 to 0,75.
• Ułamek 7/10: 7 dzielone przez 10 to 0,7.
• Ułamek 15/100: 15 dzielone przez 100 to 0,15.

Krok 3: Zamiana liczb dziesiętnych na ułamki zwykłe

Aby zamienić liczbę dziesiętną na ułamek zwykły, zapisujemy cyfry po przecinku jako licznik, a jako mianownik wpisujemy 1 z tyloma zerami, ile jest cyfr po przecinku.

Przykład:

• Liczba 0,8: 8 jako licznik, 1 zero (jedna cyfra po przecinku) jako mianownik, czyli 8/10.
• Liczba 1,25: 125 jako licznik, 2 zera (dwie cyfry po przecinku) jako mianownik, czyli 125/100.
• Liczba 0,03: 3 jako licznik, 2 zera (dwie cyfry po przecinku) jako mianownik, czyli 3/100.

Krok 4: Dodawanie i odejmowanie liczb dziesiętnych

Podczas dodawania i odejmowania liczb dziesiętnych kluczowe jest wyrównanie przecinków, czyli ustawienie ich jeden pod drugim. Następnie dodajemy lub odejmujemy cyfry tak, jak w przypadku liczb całkowitych, a na końcu przenosimy przecinek do wyniku.

Przykład dodawania:

1,23
+ 0,45
-----
1,68

Przykład odejmowania:

5,7 - 2,3 = 3,4

7,89
- 3,45
-----
4,44

Krok 5: Mnożenie liczb dziesiętnych

Mnożymy liczby dziesiętne tak, jakby nie było przecinków. Następnie liczymy łączną liczbę cyfr po przecinku w mnożonych liczbach i wstawiamy przecinek w wyniku, licząc od prawej strony.

Przykład:

0,2 * 0,3

Najpierw: 2 * 3 = 6.

W mnożonych liczbach są łącznie dwie cyfry po przecinku (jedna w 0,2 i jedna w 0,3).

Więc wynik to 0,06.

Krok 6: Dzielenie liczb dziesiętnych

Aby podzielić liczbę dziesiętną przez liczbę całkowitą, dzielimy tak, jakby nie było przecinka. Po zakończonym dzieleniu części całkowitej, wstawiamy przecinek w wyniku.

Przykład:

6,4 / 2

Najpierw dzielimy 6 przez 2, co daje 3. Wstawiamy przecinek.

Następnie dzielimy 4 przez 2, co daje 2.

Wynik to 3,2.

Praktyczne zastosowania liczb dziesiętnych:

Liczby dziesiętne są niezwykle praktyczne w życiu codziennym. Po pierwsze, używamy ich do cen towarów w sklepach. Na przykład, cena chleba może wynosić 3,50 zł. Po drugie, są one niezbędne przy pomiarach – długości, wagi, temperatury. Mówimy, że temperatura wynosi 25,5 stopnia Celsjusza, lub że wzrost danej osoby to 1,65 metra.