Sprawdzian Kals A1 Gimnazjum Matematyka Pola Figur

W Gimnazjum, nauka matematyki stanowi fundament dla dalszego rozwoju edukacyjnego ucznia. Szczególnie istotne jest opanowanie podstawowych zagadnień geometrycznych, a wśród nich pól figur płaskich. Sprawdzian z tego zakresu jest nie tylko oceną zdobytej wiedzy, ale także okazją do utrwalenia kluczowych wzorów i umiejętności praktycznego ich zastosowania. Zrozumienie, jak obliczyć pole trójkąta, kwadratu, prostokąta czy koła, otwiera drzwi do rozwiązywania bardziej złożonych problemów geometrycznych i problemów pojawiających się w codziennym życiu.

W niniejszym artykule przyjrzymy się bliżej, co zazwyczaj obejmuje sprawdzian z pól figur na poziomie gimnazjalnym. Skupimy się na kluczowych pojęciach, zaprezentujemy przykłady i podpowiemy, jak skutecznie przygotować się do takiego sprawdzianu.

Kluczowe Figury i Ich Pól

Na sprawdzianie z pól figur płaskich w gimnazjum zazwyczaj pojawiają się zadania dotyczące obliczania pola najbardziej podstawowych figur. Znajomość wzorów na ich pola jest absolutnie kluczowa.

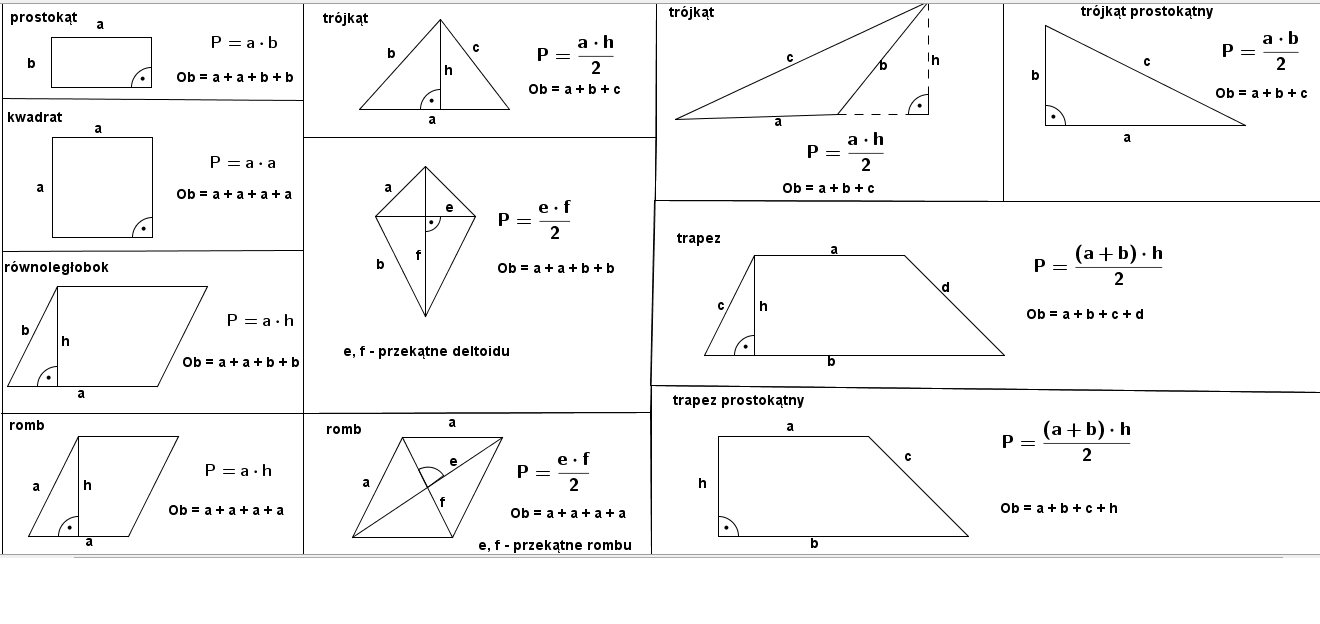
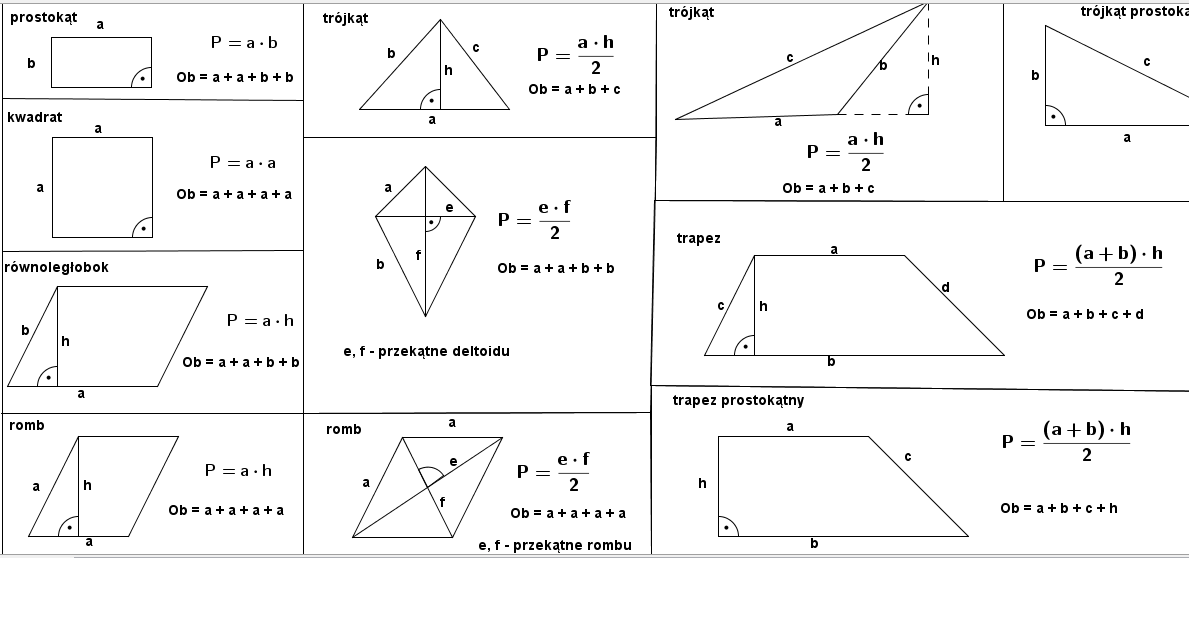
Prostokąt – Fundament Geometryczny

Prostokąt to jedna z pierwszych figur, której pole poznajemy. Jego pole obliczamy, mnożąc długość jednego boku przez długość boku przyległego. Wzór jest prosty: P = a * b, gdzie 'a' i 'b' to długości boków prostokąta.

Przykład: Jeśli mamy prostokąt o bokach długości 5 cm i 10 cm, jego pole wynosi 5 cm * 10 cm = 50 cm². Proste, prawda?

Zastosowanie tego wzoru jest wszechobecne. Od wyliczania powierzchni stołu, przez obszar dywanu, po wymiary pokoju, który chcemy pomalować – wszędzie tam przyda się znajomość pola prostokąta.

Kwadrat – Specjalny Przypadek Prostokąta

Kwadrat jest szczególnym przypadkiem prostokąta, w którym wszystkie boki mają tę samą długość. Stąd wzór na jego pole to po prostu długość boku podniesiona do kwadratu: P = a².

Przykład: Kwadrat o boku 7 metrów ma pole 7 m * 7 m = 49 m².

W praktyce kwadraty spotykamy w kształcie płytek chodnikowych, fragmentów ekranu komputera czy pól na szachownicy.

Trójkąt – Różnorodność i Elegancja

Pole trójkąta może być nieco bardziej złożone, ale podstawowy wzór jest bardzo ważny: P = (a * h) / 2, gdzie 'a' to długość boku trójkąta (nazywanego podstawą), a 'h' to wysokość opuszczona na ten bok.

Przykład: Mamy trójkąt, którego podstawa ma długość 8 cm, a wysokość opuszczona na tę podstawę wynosi 6 cm. Pole tego trójkąta to (8 cm * 6 cm) / 2 = 48 cm² / 2 = 24 cm².

Warto pamiętać, że wysokość może być poprowadzona wewnątrz trójkąta (w trójkątach ostrokątnych), na jednym z boków (w trójkątach prostokątnych) lub na przedłużeniu boku (w trójkątach rozwartokątnych). Kluczowe jest, aby wysokość była prostopadła do podstawy.

W niektórych przypadkach, szczególnie w zadaniach z trygonometrią, możemy spotkać się ze wzorem na pole trójkąta, który wykorzystuje dwie długości boków i sinus kąta między nimi: P = (1/2) * a * b * sin(γ). Jednak na poziomie gimnazjalnym zazwyczaj skupiamy się na wzorze z podstawą i wysokością.

Równoległobok – Połączenie Prostokąta i Trójkąta

Pole równoległoboku jest obliczane podobnie jak pole trójkąta, z tą różnicą, że nie dzielimy przez dwa: P = a * h, gdzie 'a' to długość jednego z boków (podstawa), a 'h' to wysokość opuszczona na ten bok.

Przykład: Równoległobok ma podstawę o długości 12 cm i wysokość równą 5 cm. Jego pole wynosi 12 cm * 5 cm = 60 cm².

Równoległobok możemy sobie wyobrazić jako "ściśnięty" prostokąt. Jego wysokość nie jest tożsama z długością boku, musi być ona prostopadła do podstawy.

Trapez – Figura z Dwoma Podstawami

Pole trapezu jest nieco bardziej skomplikowane, ponieważ ma on dwie równoległe podstawy. Wzór to: P = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości równoległych podstaw, a 'h' to wysokość trapezu (odległość między podstawami).

Przykład: Trapez ma podstawy o długościach 7 cm i 13 cm, a jego wysokość wynosi 4 cm. Pole trapezu wynosi ((7 cm + 13 cm) * 4 cm) / 2 = (20 cm * 4 cm) / 2 = 80 cm² / 2 = 40 cm².

Kluczem do poprawnego obliczenia pola trapezu jest prawidłowe zidentyfikowanie podstaw i wysokości.

Koło – Okrągła Precyzja

W przypadku koła, kluczowy jest promień (r). Wzór na pole koła to: P = π * r², gdzie 'π' (pi) jest stałą matematyczną, przybliżaną najczęściej jako 3.14 lub 22/7.

Przykład: Koło o promieniu 5 cm ma pole P = π * (5 cm)² = 25π cm². Przyjmując π ≈ 3.14, pole wynosi 25 * 3.14 cm² = 78.5 cm².

Znajomość pola koła jest ważna w wielu zastosowaniach, od projektowania okrągłych elementów, po obliczanie powierzchni tarcz zegarów czy przekrojów rur.

Zadania na Sprawdzianie

Sprawdziany z pól figur płaskich zazwyczaj obejmują różnorodne zadania:

• Obliczanie pola konkretnej figury, gdy podane są jej wymiary.
• Obliczanie brakującego boku lub wysokości, gdy znane jest pole i inne wymiary.
• Zadania złożone, które wymagają podziału skomplikowanej figury na prostsze do obliczenia.
• Zastosowania praktyczne, gdzie pole figury trzeba obliczyć w kontekście realnej sytuacji (np. powierzchnia ściany do pomalowania, ilość materiału na budowę dachu).

Często spotykane są również zadania wymagające umiejętności wyciągania wniosków z rysunku technicznego lub schematu. Dokładne czytanie polecenia jest tutaj absolutnie kluczowe.

Przygotowanie do Sprawdzianu – Skuteczne Metody

Dobre przygotowanie do sprawdzianu z pól figur płaskich wymaga systematyczności i zrozumienia materiału, a nie tylko zapamiętywania wzorów na pamięć.

1. Opanowanie Wzorów

To podstawa. Wzory na pola prostokąta, kwadratu, trójkąta, równoległoboku, trapezu i koła muszą być opanowane do perfekcji. Zapisuj je wielokrotnie, twórz fiszki, powtarzaj je w myślach.

2. Zrozumienie Wyprowadzenia Wzorów

Dlaczego pole trójkąta to (a*h)/2? Ponieważ dwa takie same trójkąty tworzą równoległobok (lub prostokąt, jeśli trójkąt jest prostokątny) o polu a*h. Dzieląc przez dwa, otrzymujemy pole pojedynczego trójkąta. Rozumienie logiki stojącej za wzorami ułatwia ich zapamiętanie i stosowanie.

3. Rozwiązywanie Różnorodnych Zadań

Nie ograniczaj się do jednego typu zadań. Ćwicz obliczenia, zadania z brakującymi danymi, a także te wymagające podziału figur. Im więcej zróżnicowanych problemów rozwiążesz, tym pewniej poczujesz się na sprawdzianie.

4. Wykorzystanie Rysunków

W geometrii rysunek często mówi więcej niż tysiąc słów. Zawsze rysuj figury, zaznaczaj dane i szukane. Ułatwia to wizualizację problemu i identyfikację odpowiednich wzorów.

5. Praca z Materiałami Dydaktycznymi

Korzystaj z podręcznika, zeszytu ćwiczeń, a także zasobów online. Istnieje wiele stron internetowych i platform edukacyjnych oferujących dodatkowe ćwiczenia i wyjaśnienia.

6. Testy Próbne

Rozwiązywanie testów próbnych z poprzednich lat lub przygotowanych przez nauczyciela, daje doskonały pogląd na to, czego można się spodziewać. Pozwala również ocenić poziom trudności i czas potrzebny na rozwiązanie zadań.

Realne Zastosowania Pol Figur

Matematyka nie jest tylko abstrakcyjną nauką. Pola figur mają mnóstwo praktycznych zastosowań:

• Budownictwo i Architektura: Obliczanie powierzchni ścian do malowania, podłóg do układania płytek, dachów do pokrycia, działek budowlanych. Architekci i budowlańcy na co dzień wykorzystują te umiejętności.
• Projektowanie Wnętrz: Dobór odpowiedniej wielkości mebli, ilość wykładziny dywanowej, rozmieszczenie elementów wystroju.
• Ogrodnictwo: Obliczanie powierzchni trawników, rabat kwiatowych, wielkości pojemników na rośliny.
• Rzemiosło i DIY: Uszycie ubrania, wykonanie mebla, stworzenie ozdoby – wszędzie tam trzeba znać wymiary i pola powierzchni.
• Nawigacja i Kartografia: Mapy często przedstawiają obszary w odpowiedniej skali, a obliczenie pola na mapie może pomóc oszacować rzeczywistą powierzchnię terenu.

Wyobraźmy sobie, że chcemy kupić farbę do pomalowania pokoju. Pokój ma wymiary 4m x 5m, a wysokość ścian wynosi 2.5m. Powierzchnia dwóch ścian to 2 * (4m * 2.5m) = 20 m². Powierzchnia dwóch pozostałych ścian to 2 * (5m * 2.5m) = 25 m². Łączna powierzchnia ścian do pomalowania to 45 m². Należy od tej powierzchni odjąć okna i drzwi, których wymiary również mogą być podane w zadaniu (np. okno 1m x 1.5m = 1.5 m², drzwi 1m x 2m = 2 m²). Całkowita powierzchnia do pomalowania to wtedy 45 m² - 1.5 m² - 2 m² = 41.5 m². Wiedząc, że puszka farby wystarcza na 10 m², potrzebujemy 41.5 m² / 10 m²/puszka ≈ 4.15 puszki. Musimy więc kupić 5 puszek farby.

To tylko jeden z wielu przykładów pokazujących, jak ważne jest opanowanie obliczania pól figur.

Podsumowanie i Zachęta

Sprawdzian z pól figur płaskich na poziomie gimnazjum to ważny etap w nauce matematyki. Opanowanie podstawowych wzorów i umiejętność ich zastosowania nie tylko pozwala uzyskać dobrą ocenę, ale przede wszystkim wyposaża ucznia w cenne narzędzia do analizowania i rozwiązywania problemów w świecie rzeczywistym. Regularne ćwiczenia, zrozumienie logiki wzorów i praktyczne podejście do nauki to klucz do sukcesu.

Nie traktujcie sprawdzianu jako celu samego w sobie, ale jako okazję do utrwalenia wiedzy i doskonalenia umiejętności. Powodzenia w nauce i na sprawdzianie! Pamiętajcie, że matematyka, choć czasem wymagająca, jest fascynującą i niezwykle użyteczną dziedziną wiedzy.