Sprawdzian Funkcja I Jej Własności

Czy kiedykolwiek zastanawiałeś się, jak przewidzieć wynik pewnego działania, mając tylko pewne dane wejściowe? Na przykład, jak na podstawie ilości godzin nauki przewidzieć swój wynik na sprawdzianie? Albo jak odległość od miejsca zamieszkania wpływa na czas dojazdu do pracy? Otóż, w matematyce istnieje narzędzie, które pomaga nam modelować i analizować tego typu relacje – to funkcja.

Zapewne słysząc słowo "funkcja" masz przed oczami skomplikowane wzory i wykresy. Rozumiem, że może to wydawać się trudne, zwłaszcza gdy zbliża się sprawdzian. Ale obiecuję, że wspólnie przejdziemy przez ten temat krok po kroku, zrozumiejąc, czym funkcja jest i jakie ma właściwości. Celem tego artykułu jest przygotowanie Cię do sprawdzianu z funkcji i ich właściwości w sposób przystępny i efektywny.

Co to jest funkcja?

Najprościej mówiąc, funkcja to przyporządkowanie, które każdemu elementowi z jednego zbioru (nazywanego dziedziną) przypisuje dokładnie jeden element z innego zbioru (nazywanego przeciwdziedziną lub zbiorem wartości). Można to sobie wyobrazić jako maszynę, do której wrzucasz coś (dane wejściowe), a ona przetwarza to i "wyrzuca" coś innego (wynik).

Przykład: Funkcja f(x) = x + 2. Jeśli wrzucimy do niej liczbę 3 (x = 3), to otrzymamy f(3) = 3 + 2 = 5. Czyli funkcja przypisuje liczbie 3 liczbę 5.

Kluczowe jest to "dokładnie jeden". Oznacza to, że dla każdego x w dziedzinie, funkcja musi zwracać tylko jeden wynik. Jeśli dla jednego x mielibyśmy dwa różne wyniki, to nie byłaby to funkcja!

Jak sprawdzić, czy mamy do czynienia z funkcją?

Najprostszym sposobem jest analiza wykresu. Stosujemy tzw. test linii pionowej. Jeśli narysujemy dowolną linię pionową na wykresie i przetnie ona wykres w więcej niż jednym punkcie, to nie jest to funkcja. Wynika to z faktu, że dla jednego x mielibyśmy więcej niż jeden odpowiadający mu y.

Własności funkcji

Funkcje posiadają wiele ważnych właściwości, które pomagają nam je analizować i wykorzystywać. Oto kilka z nich, które prawdopodobnie pojawią się na Twoim sprawdzianie:

Dziedzina funkcji (D): Zbiór wszystkich x, dla których funkcja jest określona. Innymi słowy, wszystkie wartości, które można "wrzucić" do funkcji.
Zbiór wartości funkcji (ZW): Zbiór wszystkich y, które funkcja może "wyrzucić".
Miejsca zerowe funkcji: Wartości x, dla których f(x) = 0. Graficznie, są to punkty przecięcia wykresu z osią OX.
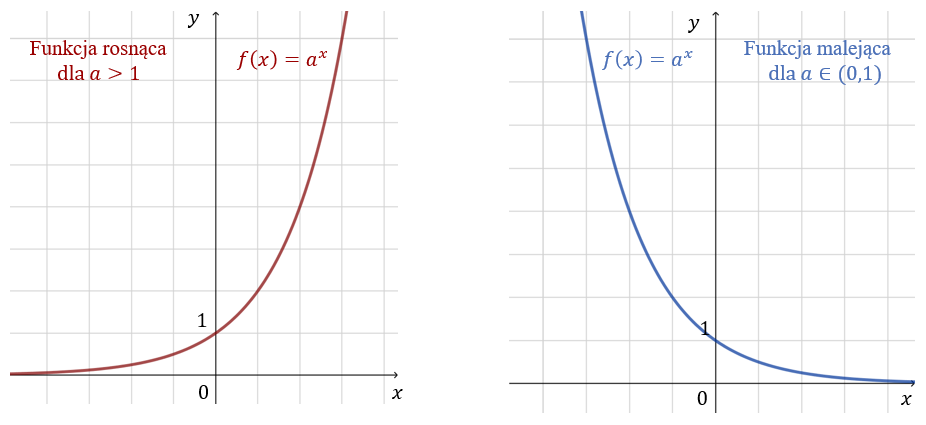
Monotoniczność funkcji: Określa, jak zmienia się wartość funkcji wraz ze wzrostem wartości argumentu x. Funkcja może być:
- Rosnąca: Wraz ze wzrostem x rośnie również f(x).
- Malejąca: Wraz ze wzrostem x maleje f(x).
- Stała: Wartość f(x) nie zmienia się wraz ze zmianą x.
Ekstrema funkcji: Maksima i minima funkcji.
- Maksimum (lokalne/globalne): Największa wartość funkcji w danym przedziale (lokalne) lub w całej dziedzinie (globalne).
- Minimum (lokalne/globalne): Najmniejsza wartość funkcji w danym przedziale (lokalne) lub w całej dziedzinie (globalne).
Parzystość i nieparzystość funkcji:
- Funkcja parzysta: f(-x) = f(x) dla każdego x z dziedziny. Wykres funkcji parzystej jest symetryczny względem osi OY.
- Funkcja nieparzysta: f(-x) = -f(x) dla każdego x z dziedziny. Wykres funkcji nieparzystej jest symetryczny względem początku układu współrzędnych.

Dziedzina funkcji – na co uważać?

Określanie dziedziny funkcji jest bardzo ważne. Trzeba pamiętać o kilku ograniczeniach:

Dzielenie przez zero: Mianownik ułamka musi być różny od zera.
Pierwiastek kwadratowy (i pierwiastki parzystego stopnia): Wyrażenie pod pierwiastkiem musi być większe lub równe zero.
Logarytmy: Argument logarytmu musi być większy od zera.

Przykład: Jaka jest dziedzina funkcji f(x) = 1 / (x - 2)? Mianownik nie może być równy zero, więc x - 2 ≠ 0, czyli x ≠ 2. Zatem dziedziną funkcji jest zbiór wszystkich liczb rzeczywistych z wyjątkiem liczby 2, czyli D = R \ {2}.

Jak przygotować się do sprawdzianu?

Oto kilka praktycznych wskazówek, które pomogą Ci dobrze przygotować się do sprawdzianu z funkcji i ich właściwości:

Powtórz definicje: Upewnij się, że rozumiesz, czym jest funkcja, dziedzina, zbiór wartości, miejsce zerowe, monotoniczność, ekstrema, parzystość i nieparzystość.
Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej utrwalisz sobie wiedzę. Zacznij od prostych przykładów i stopniowo przechodź do bardziej skomplikowanych.
Analizuj wykresy: Naucz się odczytywać z wykresu dziedzinę, zbiór wartości, miejsca zerowe, przedziały monotoniczności i ekstrema funkcji.
Pytaj! Jeśli masz jakieś pytania lub wątpliwości, nie bój się pytać nauczyciela lub kolegów.
Korzystaj z zasobów online: W Internecie znajdziesz wiele materiałów edukacyjnych, w tym filmów instruktażowych, interaktywnych ćwiczeń i arkuszy kalkulacyjnych, które mogą pomóc Ci w nauce.
Zrób sobie przerwę: Nie ucz się na ostatnią chwilę! Rozłóż naukę na kilka dni i rób sobie regularne przerwy. Twój mózg potrzebuje czasu na przetworzenie informacji.

Pamiętaj! Kluczem do sukcesu jest zrozumienie, a nie tylko zapamiętywanie wzorów. Staraj się zrozumieć, dlaczego dana funkcja ma takie, a nie inne właściwości. To pomoże Ci nie tylko na sprawdzianie, ale również w dalszej nauce matematyki.

Przykładowe zadania (z rozwiązaniami)

Zadanie 1: Określ dziedzinę funkcji f(x) = √(x - 3).

Rozwiązanie: Wyrażenie pod pierwiastkiem musi być większe lub równe zero, czyli x - 3 ≥ 0. Zatem x ≥ 3. Dziedzina funkcji to D = [3, +∞).

Zadanie 2: Określ miejsca zerowe funkcji f(x) = x² - 4.

Rozwiązanie: Miejsca zerowe to wartości x, dla których f(x) = 0. Zatem x² - 4 = 0. Możemy to zapisać jako (x - 2)(x + 2) = 0. Zatem x = 2 lub x = -2. Miejsca zerowe funkcji to x = 2 i x = -2.

Zadanie 3: Zbadaj monotoniczność funkcji liniowej f(x) = 2x + 1.

Rozwiązanie: Funkcja liniowa f(x) = ax + b jest rosnąca, gdy a > 0, malejąca, gdy a < 0, a stała, gdy a = 0. W tym przypadku a = 2 > 0, więc funkcja jest rosnąca na całej swojej dziedzinie.

Wierzę w Ciebie! Z odpowiednim przygotowaniem i zrozumieniem tematu, na pewno poradzisz sobie na sprawdzianie z funkcji i ich właściwości. Powodzenia!